探究抓牌游戏的数学奥秘

●

(瑞安市锦湖第一中学 浙江温州 325200)

●李家祥

(瑞安市安阳实验中学 浙江温州 325200)

探究抓牌游戏的数学奥秘

●李子法

(瑞安市锦湖第一中学 浙江温州 325200)

●李家祥

(瑞安市安阳实验中学 浙江温州 325200)

有一个非常有趣的抓牌游戏，规则是：54张扑克牌，甲、乙2个人轮换抓，一次可抓1～4张牌，谁抓到最后1张谁就输.在游戏中,笔者发现了保持胜出的办法以及蕴含的数学思想方法，探讨如下：

1 分析与探究

怎样保持胜出呢？

不妨设甲第一个抓牌.先从最后剩5张牌开始研究，甲抓走4张，剩下1张，甲就会赢.

最后剩6张牌时，若甲抓1张，乙抓4张，剩下1张，甲只能抓走最后1张就输了；若甲抓2张，乙抓3张，剩下1张，甲就输了；若甲抓3张，乙抓2张，剩下1张，甲就输了；若甲抓4张，乙抓1张，剩下1张只能由甲抓走，甲就输了.综合4种情况发现：最后剩6张牌时，谁先抓谁就输，而乙赢的方法就是所抓的牌数加上甲的牌数等于5，剩下最后1张，甲非抓不可.

同理，最后剩下7张牌时甲先抓1张，最后8张牌时甲先抓2张，最后9张牌时甲先抓3张，最后10张牌时，甲先抓4张，……，这样，甲再抓牌时只要与乙的牌数凑成5，则一定会赢.但最后剩下11张牌时，无论甲抓几张，只要乙抓的牌数与甲的牌数凑成5，则甲一定会输.最后剩下12张牌时甲先抓1张，最后13张时甲先抓2张，最后14张时甲先抓3张，最后15张时，甲先抓4张，……，这样，甲再抓牌时，所抓的牌数只要与乙的牌数凑成5，则一定会赢.但最后剩下16张牌时，无论甲抓几张牌，只要乙所抓的牌数与甲的牌数凑成5，则甲一定会输.

由此得出一个有趣的规律：当牌数是6，11，16，…时，无论甲抓几张，只要乙所抓的牌数与甲的牌数凑成5，则甲一定会输；而当其他牌数时，甲都有办法必赢.因为54÷5=10余4(9张牌和14张牌时类似)，所以甲先抓3张牌，甲再抓牌时只要与乙的牌数凑成5，那么到最后只剩下1张牌给乙，甲就可保持胜出.

通过以上研究，得到结论：若游戏规则是“甲、乙2个人轮换抓，一次可抓1～4张，谁抓到最后1张谁就输”，那么当扑克牌数减去1的差能被5整除时，先抓的人必输；当扑克牌数减去1的差不能被5整除时，先抓的人必赢.

2 问题的拓展

还是54张扑克牌，若改变游戏规则如下：甲、乙2个人轮换抓，一次可抓1～5张，谁抓到最后1张谁就输.有没有保持胜出的办法呢？

不妨设甲先抓牌.因为54被6整除，所以甲只要先抓5张牌，无论乙抓几张，甲再抓时所抓的牌数只要与乙的牌数凑成6，最后剩下1张给乙，甲就可保持胜出.

此类问题有没有其他的求解方法呢？

可试一试倒推法.为了叙述方便，把54张扑克牌编上号，分别为1～54号，按编号从小到大抓扑克牌.甲为了取胜，必须把54号扑克牌留给乙，因此甲在最后一次抓扑克牌时，序号最大的一张必须是53.为了保证能做到这一点，就必须使乙在倒数第2次抓牌时的序号为49(53-4)～52(53-1).因此，甲在倒数第2次抓扑克牌时，序号最大的一张必须是48.为了保证能做到这一点，就必须使乙在倒数第3次抓牌时的序号为44(48-4)～47(48-1).因此，甲在倒数第3次抓牌时，序号最大的一张必须是43，…，把甲每次抓牌的最大序号从尾到首排列：53，48，43，…，观察发现这是一个等差数列，公差d=5，且这些数被5除都余3.因此，甲第一次抓牌时应抓1～3号牌，然后乙抓a张牌，因为a+(5-a)=5，所以为确保甲从一个被5除余3的数到达下一个被5除余3的数，甲就应抓5-a张牌.这样就能保证第一个抓牌的人必胜.

3 问题的启示

这个游戏在探究过程中用到2 种数学思想方法：首先是从特殊到一般、简单到复杂的归纳递推方法，其次是采用倒推的逆向思维方法.这2种数学思想方法是解决疑难问题的2把金钥匙，只要学会运用，许多困难都会迎刃而解.

3.1 归纳递推方法

例1平面上5条直线最多能把圆的内部分成几部分？平面上100条直线最多能把圆的内部分成几部分？

分析如果直接画图解答，那么寻求问题的答案就很困难；如果先“退”到问题最简单的情况开始观察，逐步归纳并猜想一般的递推公式，问题就迎刃而解了.

解用ak表示k条直线最多能把圆的内部分成的部分数，k=0，1，2，….如图1所示:a0=1，a1=a0+1=2，a2=a1+2=4，a3=a2+3=7，a4=a3+4=11，…

图1

归纳出递推公式an+1=an+n，即画第n+1条直线时，最多增加n部分.原因是：第1条直线最多把圆分成2个部分，故a1=2.当画第2条直线时要想把圆内部分割的部分尽可能多，就应和第1条直线在圆内相交，交点把第2条直线在圆内部分分成2条线段，而每条线段又把原来的一个区域划分成2个区域，因而增加的部分数是2，正好等于第2条直线的序号.同理，当画第3条直线时，要想把圆内部分割的部分数尽可能多，就应和前2条直线在圆内各有一个交点，2个交点把第3条线在圆内部分成3条线段，而每条线段又把原来一个区域划分成2个区域，因此增加的部分数是3，正好等于第3条直线的序号，….这个道理适用于任意多条直线的情形，因此递推公式an+1=an+n是正确的.

这样5条直线最多把圆内分成

a5=a4+5=11+5=16(部分).

要想求出100条直线最多能把圆内分成多少个部分，不能直接用递推公式，可把递推公式变形为：

an=an-1+n=an-2+(n-1)+n=

an-3+(n-2)+(n-1)+n=

…

1+1+2+3+4+…+n=

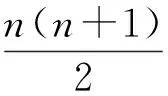
故

3.2 逆向思维方法

例2甲、乙、丙3个人各有铜钱若干枚，开始，甲把自己的铜钱拿出一部分分给了乙、丙，使乙、丙的铜钱数各增加了1倍；后来，乙也照着甲的方法做，拿出自己的一部分给甲和丙，使甲、丙的铜钱数各增加了1倍；最后，丙也照着这样的方法做，使甲、乙的铜钱数各增加了1倍；这时3个人的铜钱数都是8枚.问原来甲、乙、丙3个人各有铜钱多少枚？

分析往往首先会考虑常规方法，直接列算式或列方程解答，但非常繁琐复杂.如果能从结果出发逆向思考，利用倒推法便能求得结果.

解根据3个人最后的铜钱数都是8枚来列表倒推，如表1所示：

表1 甲、乙、丙的铜钱数

故原来甲有铜钱13枚，乙有铜钱7枚，丙有铜钱4枚.

综上所述，抓牌游戏中蕴含的这2种数学思想方法无论在理论上还是实践中都有广泛的应用，具有很高的研究价值.

[1] 黄东坡.数学培优竞赛新方法(七年级)[M].武汉：湖北人民出版社，2009.