通性通法与高考数学解题的万能模式

●过伯祥 (浙江海洋学院数理与信息学院 浙江舟山 316000)

1 高观点下的中学数学

数学是什么?“一切数学学科的决定性特点总是某种形式化的方法”(辛钦)，“数学为科学研究提供简明精确的形式化语言”.从一定意义上说，数学是一门形式科学.《数学课程标准》与它的解读中，也强调要这样认识数学：“把数学看成是一系列数学地组织现实世界的人类活动，即用数学的思想与方法，不断把与实际问题有关的材料进行整理和组织起来的活动.”《标准》中数学学习内容的6个核心概念：数感、符号感、空间观念、统计观念、应用意识、推理能力.其中说到，“符号表示是人类文明发展的重要标志之一，数学课程的一个任务就是使学生感受和拥有使用符号的能力”.

中学数学的主要形式是：方程、不等式、算式与函数式.概括地说，数学解题总是这样两大步骤：把问题进一步形式化(最终列出方程、不等式，算式、函数式);然后进行合乎数学规范的形式操作.

例1 设等差数列{an}(n≥1)包含1和.证明：{an}中任意3项均不构成等比数列.

分析本题解题过程的本质就是：首先，用形式符号表达出满足条件的数列中的任意3项;然后，通过形式推理(这里用的是反证法)说明结论成立.

证明设ak=1，al=，数列的公差为d.

用反证法，设am，an，ar构成等比数列.据此列出算式，进行运算推导，得出矛盾am=an=ar，从而完成证明.事实上，

假定 am，an，ar构成等比数列，则

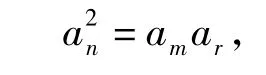
由此得

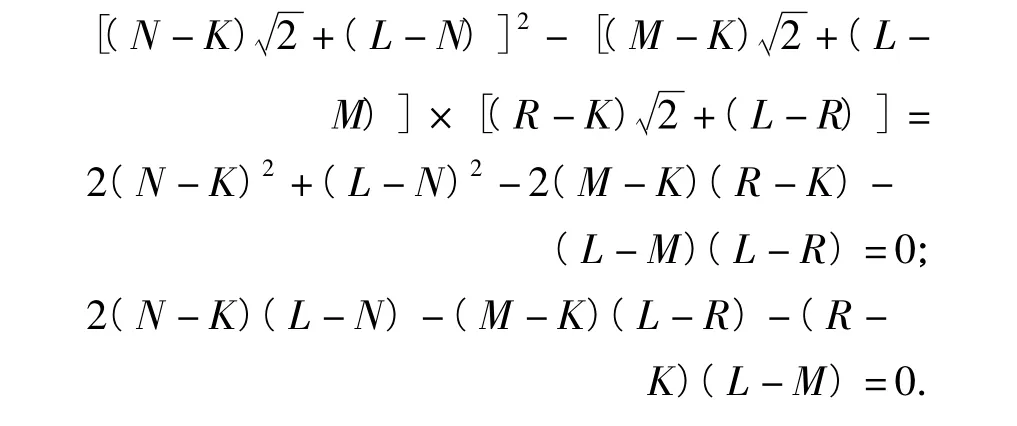
由此可推出M=N=R，即am=an=ar，矛盾.因此结论成立.

评注本例是一道证明题.形式符号设定，数列的任意3项表示出来后，过程中的大部分内容，即为(运用等式运算性质的)算式的形式推导.其中的要点是：选择哪几个量为主变量;过程中如何适当地运用变量代换，以简化过程;主要借助于有理数加无理数的特殊性质引出矛盾，说明道理.

2 中学数学中的通性通法

“通性通法”最早是由美籍华人数学家项武义教授在主编一套初中数学实验教材中提出来的.后来，这种提法就风行开了.然而很多人认为“常用多用的性质方法，就是通性通法”.因此，应该先对“通性通法”作一界定.

中学数学，特别是高中数学，有十多个系统领域.每一个领域中的内容，一般说，可以分为两大部分：一部分是本领域专属的新学的定义、性质与方法，即其自身独特的概念、性质、符号体系与形式变换常用的方法技巧;另一部分是己学的通用常用的性质方法.这后一部分，“用通性通法操作”式子(方程、不等式、函数式)的原理、变换与运算，便是数学的通性通法.这样的通性通法是确确实实存在着的.

多数数学问题需要通过方程求解;通常通过不等式求某变量的取值范围;通过算式求值;通过函数研究变量的变化规律.因此，中学数学的四大基本形式是：方程、不等式、算式与函数式.

3 从笛卡儿模式到高考数学解题的万能模式

(1)约三百七十多年前，近代著名的法国哲学家、数学家笛卡儿曾试图要创造万能的方法，来解决数理上的一切问题.他的这个“万能方法设想”，画成模式图可以表示如下：

这样一个常用的统一处理数学问题的方式，著名数学家波利亚后来把它叫做笛卡儿模式.

(2)通过分析大量的高考数学试题与高考模拟卷中的试题，发现高考数学解题中最常用的通法是：把问题的条件通过种种途径，化为4种基本形式(方程、不等式、算式和函数式);然后，再对它们进行计算、变换、求解.

(3)又注意到：从高考数学命题的指导思想与原则的一系列提法：“发挥数学作为基础学科的作用，既重视考查中学数学的掌握程度，又注意考查进入高校继续学习的潜能”，命题“坚持多角度、多层次的考查;注重对基础知识的考查;……同时兼顾试题的基础性、综合性和现实性，重视试题设计的层次性，合理调控综合程度”，“期望整卷难度系数控制在0.6～0.65之间;……考查内容，要求既有一定的覆盖面，又突出重点内容和主干知识;……问题设计力求入口宽，有层次;……重视数学概念、数学本质、数学思想和解决数学问题的常规方法.”

(4)从高考试题的整个命题过程来看，它就是命题人员在命题指导思想与原则的指引与约束下，对供题人提供的题目，在命题审题会议上，就程序的多寡、难易与创新性等，进行评估、评价、讨论、修改，在这样的权衡、争洽过程中，一步步地磨出来的.命题人员们磨什么?在整体的问题情境、内容范围等确定后，就是磨小题与程序的具体安排与设计.考题，本来就是这样“命”出来的，聪明的应考人也就应该顺着这样一条路去探索思考.

作者还查阅过笛卡尔《方法论》的各个版本，并己把它应用在如下的制表中.如今这张“新解题表”，是以笛卡尔的万能方法设想为基干思想，仿照波利亚的“怎样解题表”，适应高考数学试题程序化的结构特点而制成的.这是一份针对程序化试题编制的更好用的“怎样解题表”(如图1)，是笛卡尔万能方法设想在现代中国(程序化考试题)的高考中的参考应用.

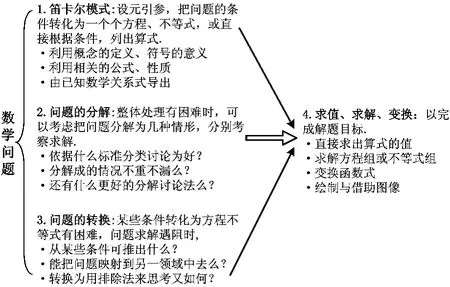
图1

例2 如图2，抛物线y=ax2+bx+c与x轴的一个交点A在点(-2，0)和(-1，0)之间(包括这2个点)，顶点C是矩形DEFG(包括边界与内部，它内部的点的横坐标在1与3之间;纵坐标在2与3之间)上的一个动点.求a的取值范围.

分析笛卡儿万能思路模式的2个步骤：(1)设定一个或几个未知量与参量，把所有的条件都用方程、不等式表示出来;(2)通过消元、代换、运算、变换，设法解出这个混合组.关键是设哪几个量为主变量，以及怎样表示出各个条件的问题.

解法1 设 A(x1，0)，另一交点 B(x2，0).如图 2，因为 a ＜0，x1为二次方程的小根，从而

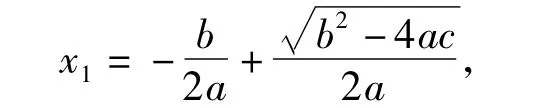
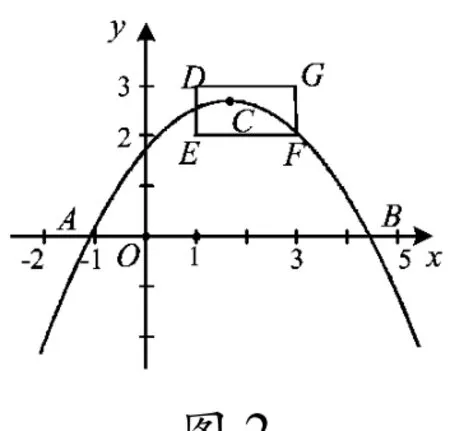
图2

于是，问题转化为：

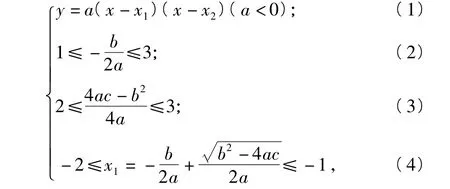
求a的取值范围.

由式(1)，式(2)，得

由式(1)，式(3)，得

式(2)-式(4)，再两边平方得

由式(6)，式(7)得

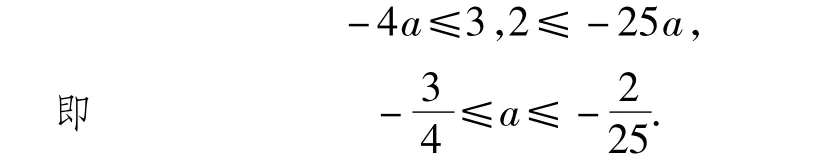
解法2 考虑开口最大、最小这2种极端情形：以 D(1，3)为顶点，过点(-1，0)的抛物线为

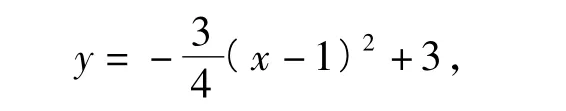
以 F(3，2)为顶点，过点(-2，0)的抛物线为

评注本例是不等式组的求解.整个过程，用适当的符号列出式子后，主要就是形式符号算式的变换与推导.解法1虽是典型的形式推演，但它的运算推导途径较难选择，等价性的理由亦较含糊、隐晦.

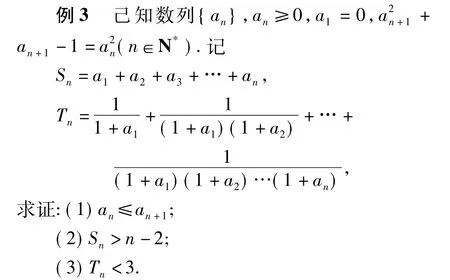
(2008年浙江省数学高考理科试题)

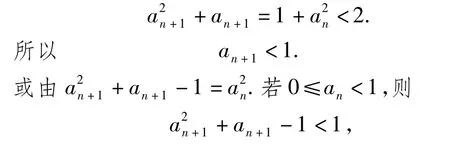
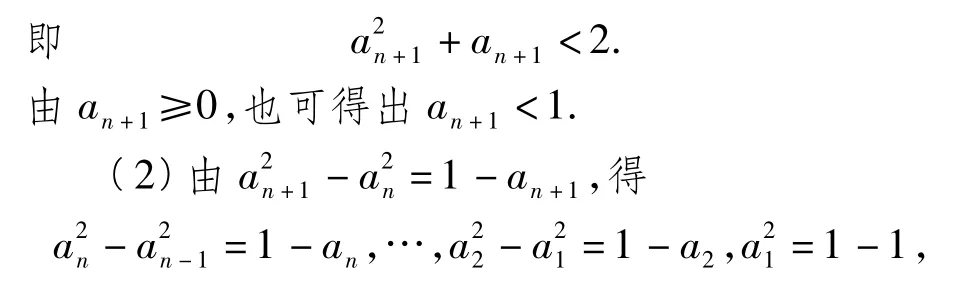
上述式子全部相叠加，得

由 an＜1，化简即得 Sn＞n-2.

上述(n-2)个式子交叉相乘得

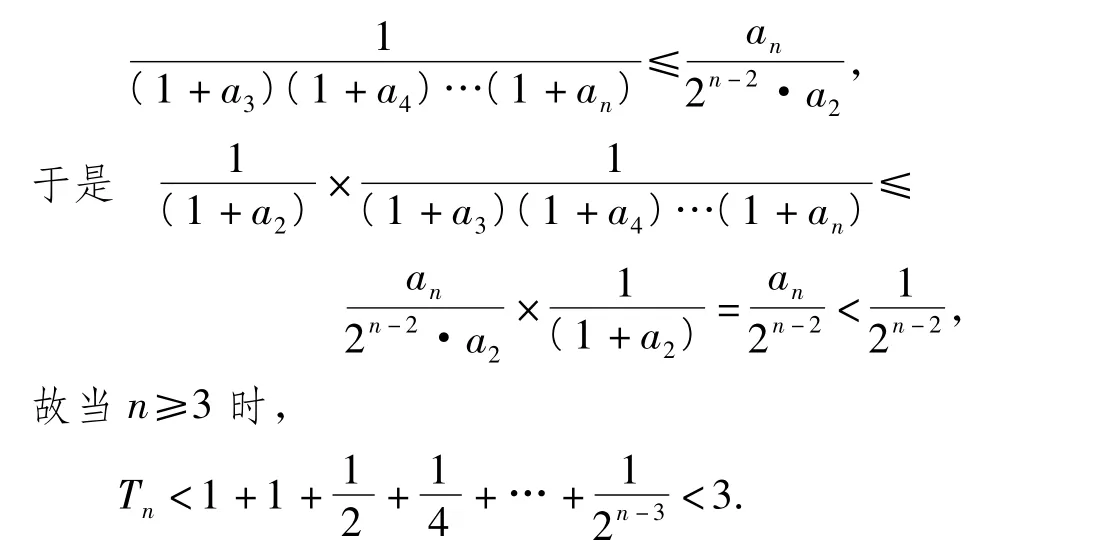
又因为 T1＜T2＜T3，所以 Tn＜3.

4 对高考数学教学的指导意义

据此万能思路，教师在教学中重点是分析，并要让学生掌握常用的把条件转化为方程、不等式的办法;掌握常用的解方程、不等式组，变换推演算式、函数式的方法技巧;掌握常用的分解讨论、映射转换方法及其注意点.因为学生的困难往往在于：某几个条件没法把握，从而列不出与它相关的方程或不等式;或是解方程、不等式组，变换某个算式的某些特殊方法技巧掌握得不太好，临场没想到.

可以注意与预测到，创新试题主要就是情景创新与条件创新.方向可以预见，具体的内容很难猜测到.笔者深信，一些重点高中的名师，必有应对创新试题方面的不可轻易外传的指导经验.