例谈从二次函数中培养学生的直觉思维

●骆银海 (牌头中学 浙江诸暨 311825)

数学思维可以分为逻辑思维和直觉思维，逻辑思维用于证明，直觉思维用于发明.新课标十分强调学生创新意识与创新能力的培养，直觉思维是数学创造与创新的基础.因此，如何培养学生的数学直觉思维至关重要.从解题教学来看，数学直觉思维也可理解为一看到题目时的题感，题感在一定程度上是可以后天培养的，每个人的数学直觉通过训练可以不断提高.

二次函数作为中学生应用最广泛的初等函数，也是最简单的非线性函数，具有许多优美的性质，是数学命题者感兴趣的考点之一.试题中背景设计之精巧、过程之流利、答案之美妙常引起师生的共鸣.笔者有幸参与了诸暨市说题展示和浙江省数学教师教学能力评比与观摩活动，颇有体会：在解决二次函数问题中可大力培养学生的直觉思维，也就是说增强学生的题感，迅速获得接近正确答案的思路和方法.现举例如下：

例1 已知函数f(x)=|x2-2x-3|，若x2＞x1＞1且f(x1)=f(x2)，求x1+x2的取值范围.

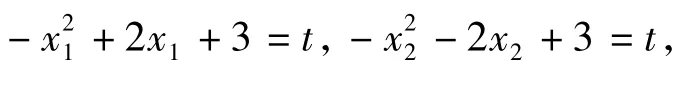
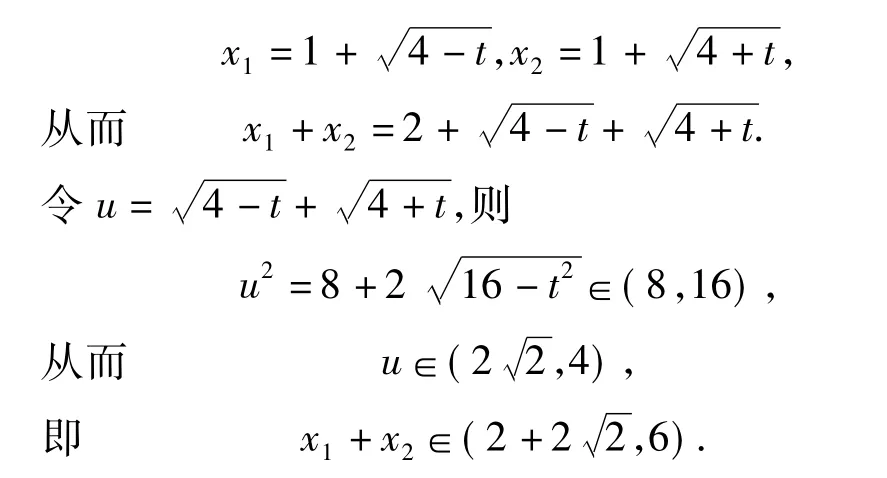
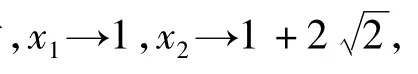
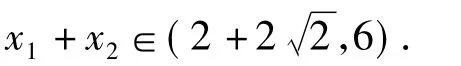
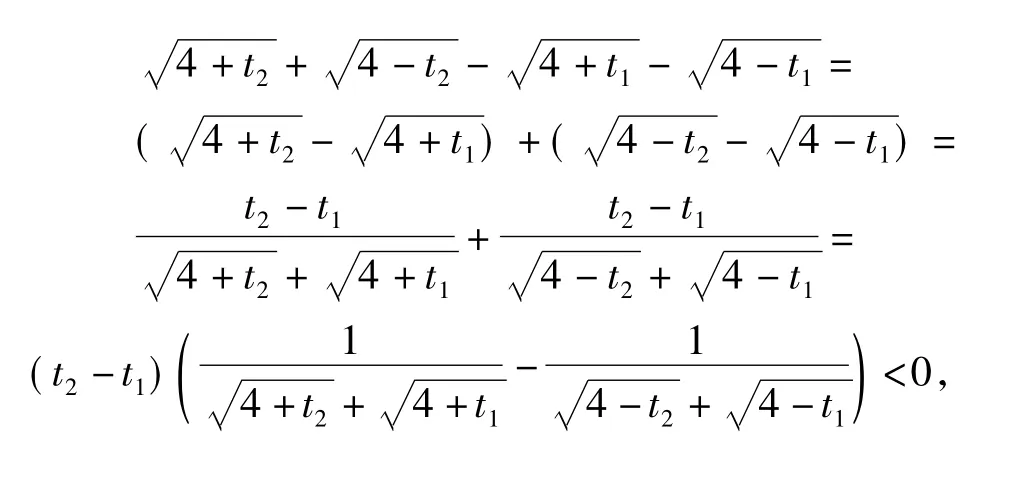
反思 本题是诸暨市高三数学二模考试试题，正确率不高，有些同学做了很长时间也没做对，有些同学一拿到题目，题感较好，马上想到：是否存在2个极端位置，很快就有了答案.可见，数学直觉思维活动在时间上表现为快速性，在过程上表现为跳跃性，在形式上表现为简约性，简约美体现了数学的本质.直觉思维是一瞬间的思维火花，是长期积累的一种升华，是思维者的灵感和顿悟，是思维过程的高度简化.

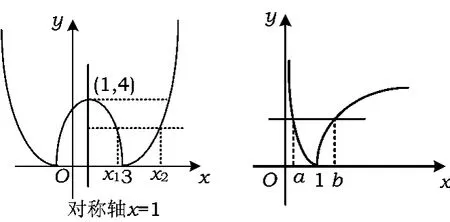
图1 图2

不仅仅在二次函数背景中可考虑直觉思维，类似地，在对数函数背景中也如出一辙.

2010年全国数学高考理科试题第10题是这样设计的：

例2 已知函数F(x)=|lgx|，若0＜a＜b，且f(a)=f(b)，则a+2b的取值范围是 ( )

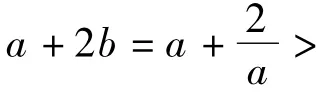
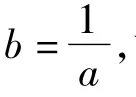
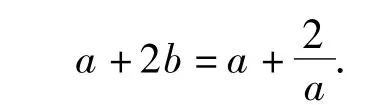
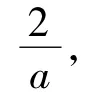
直觉思维培养 显然a+2b→+∞.若能考虑到a+2b的最小值是当f(a)=f(b)→0时取到，再结合简单的证明，那解题就变得既快又准，可以体会到直觉思维带来的好处.

例3 设t为常数，函数f(x)=|x2-2x-t|在区间［0，3］上的最大值为2，求 t的值.

(2008年浙江省数学高考理科试题)

分析由函数g(x)=x2-2x-t的对称轴是x=1且 g(0)=g(2)=-t，可得 f(0)=f(2).分析可知，f(x)在区间［0，3］上的最大值是f(1)或f(3).

若 f(1)≥f(3)，则

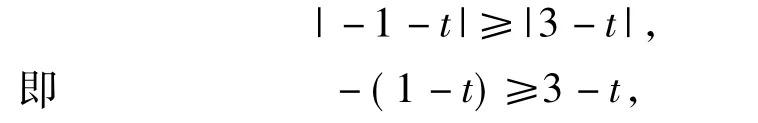
从而当t≥1时，-(-1-t)=2，解得t=1;若 f(3)≥f(1)，则

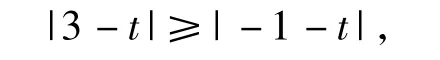
从而当 t≤1 时，|3-t|=2，解得 t=1.

综上所述，t=1.

直觉思维培养 本题是在二次函数的基础上加了绝对值函数，-t实质是函数x2-2x的上下平移.结合导数知识fmax(x)=max{端点值，极值}，由于对称轴x=1在已知的区间内，因此翻折后无论产生怎么样的形状，f(x)取到的最大值一定产生于端点值f(0)，f(3)及极值f(1)中，即

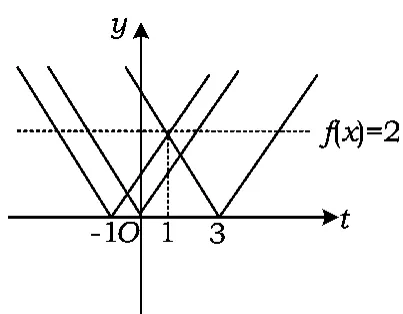
图3

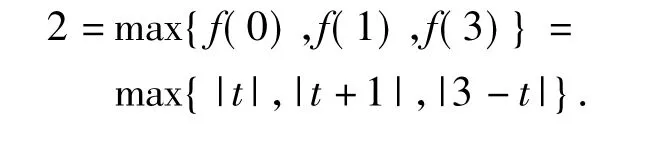
如图3，当f(x)=2时，由直觉思维知，t=1满足题意.

反思 直觉思维是基于研究对象的整体把握，不专于细节的推敲，是思维的大手笔，从而使认知结构向外扩展，因此直觉思维具有反常规的独创性.

例4 已知二次函数 f(x)=ax2+bx+c，a∈N*，c≥1，a+b=c≥1 且方程 ax2+bx+c=0 有2个小于1的不等正根，求a的最小值.

解法1 如图4，由根的分布知

由b2-4ac＞0得

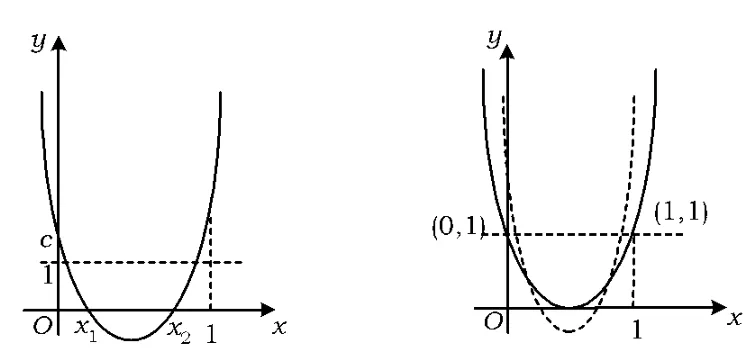
图4 图5

解法2 如图5，由题意设

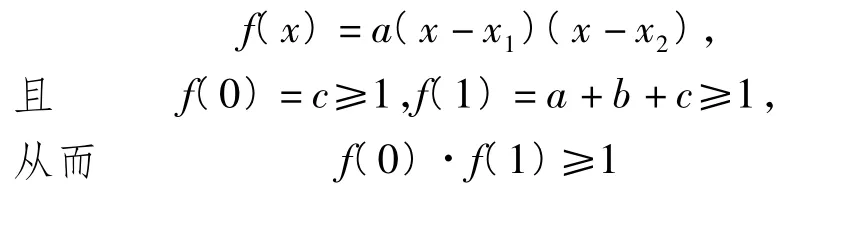
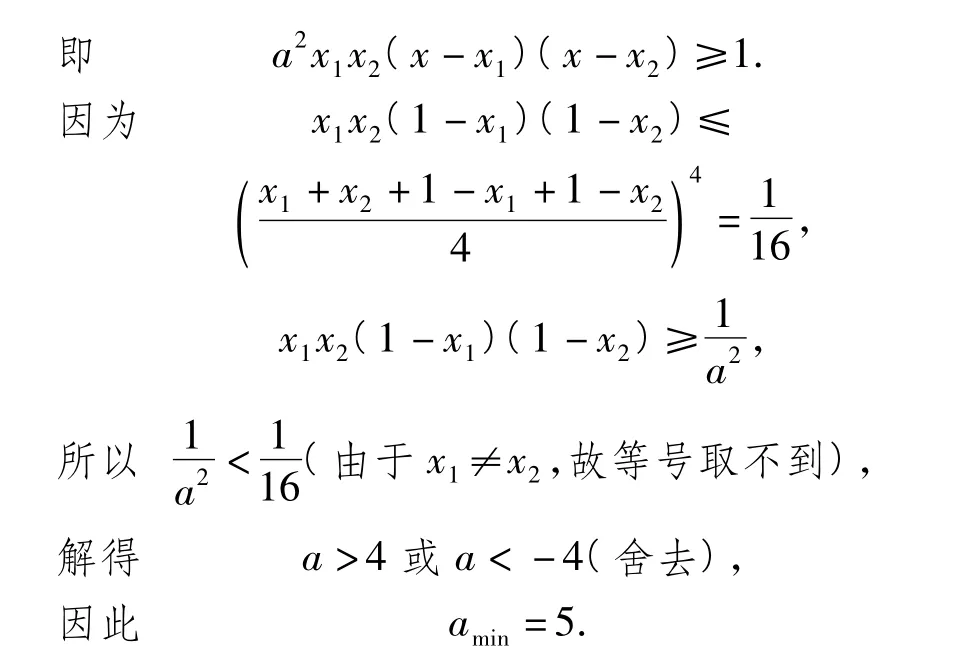
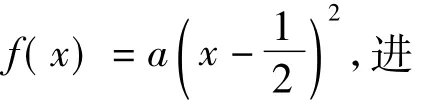
反思 数学直觉思维的表现形式是以已有的知识、经验和技能为基础，通过观察、联想、类比、归纳、猜测之后，对研究对象作出较迅速直接的判断，它不受固定的逻辑约束，能以高度省略、简化和浓缩的方式洞察数学关系，能快速解决有关数学问题.

直觉思维对培养学生的创造力相当重要，而二次函数又是非常好的训练背景，平时教师要强调：直觉思维虽具有创造精神，但由直觉思维得到的猜想需要经过逻辑方法加以验证、猜想或被证明、被推翻.此外，直觉思维能力的形成是一个渐进的过程，不能操之过急.学生的猜想错误后，应鼓励学生重新猜想.总之，只要长期坚持训练，学生的直觉思维能力就能不断得到提高，同时学生敏捷的思维和较强的知识综合运用能力得到逐步培养.这不仅有利于智力开发，更有利于逻辑思维的培养、数学能力的提高.

［1］ 沈志明.二次函数的另类最值求法及其引申［J］.中学教研(数学)，2010(5)：15-16.

［2］ 胡耀宇.抓住图象就抓住了二次函数的关键［J］.中学数学教学参考，2006(9)：20-21.

［3］ 唐恒钧.案例的视角：几何实验与几何证明［J］.中学数学杂志，2005(4)：16-17.