解三角函数题常见的几种错误

●谢黎静 (杭州师范大学附属中学 浙江杭州 310030)

三角函数是高中数学中的重要知识点，也是高考考查的热点.高考的考查分值为20分左右，题目难度适中，学生易得分，但也易失分.究其失分原因，不是三角公式应用不够熟练，不是三角函数性质掌握不全;不是题目入手太难，而是“乱花渐欲迷人眼”，即没有注意三角函数题中的隐含条件.那么，怎样挖掘隐含条件避免失分呢?笔者在完成三角函数这一教学内容后，布置了几道有关三角函数的题目，现把学生中常见的错误解法归类分析如下：

1 根据条件不能正确落实角的范围

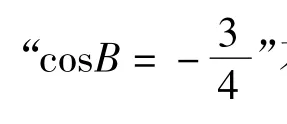
表明∠B是钝角，从而∠A是锐角，cosA＞0.

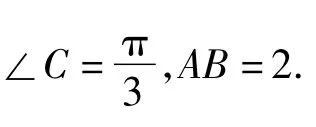
分析错解应用了正弦定理把边AC，BC与∠B建立了函数关系，然后运用三角公式建立y与x的函数关系.由于对锐角三角形内角范围这一隐含条件挖掘不够，导致结果错误.事实上，已知条件“锐角三角形”不仅直接表明∠B的范围，也隐含表明∠A的范围.

与例2类似，数学高考中出现过的题目还有：1.在锐角△ABC 中，BC=1，∠B=2∠A，则 AC的取值范围是_______.

(2009年湖南省数学高考文科试题)

2.设锐角△ABC的内角A，B，C的对边分别为a，b，c，其中 a=2bsinA，求 cosA+sinC 的取值范围.

(2007年全国数学高考理科试题)

(2011年全国数学高考理科试题)

2 根据条件不能适当缩小角的范围

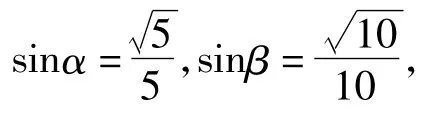
(2009年四川省数学高考文科试题)

因为α，β都是锐角，所以0＜α+β＜π，从而

因为正弦、余弦、正切函数有各自的函数性质，所以要缩小α，β的范围，从而确定α+β的值.正解2利用正、余弦在不同象限上对应的符号或值来判别角的大小.数学高考中出现过的与例3类似的题目有：

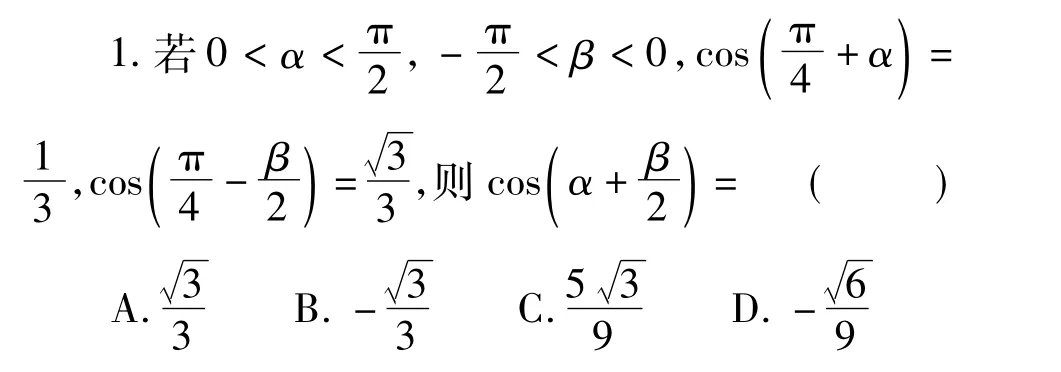
(2011年浙江省数学高考理科试题)

例4 已知 2sin2α +3sin2β =sinα，求 sin2α +sin2β的取值范围.

3 对三角形边关系认识不清

(2008年江苏省数学高考试题)

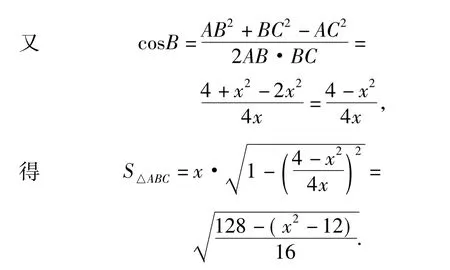
因为x＞0且128-(x2-12)≥0，所以

分析运用面积公式和余弦定理，建立面积与边之间的函数关系，这个解题思路是正确的.由于没有注意三角形边之间大小关系这个隐含条件，导致结果错误.事实上，设BC=x，AC=x，直接表明这两条边的关系以及x＞0，且隐含表明三角形中两边之和要大于第三边，即

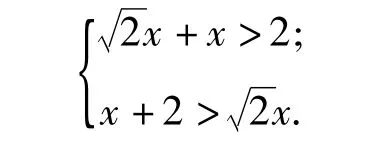
正解 由分析得

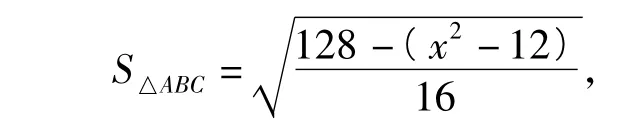
由三角形三边关系得

数学高考中出现过的与例5类似的题目还有：

(1)求△ABC的周长;

(2)求cos(A-C)的值.

(2011年湖北省数学高考理科试题)

综上所述，要提高学生解题的正确率，除了要注意题中的隐含条件外，教师在选择例题讲解时要引导学生挖掘隐含条件，避免各种错误.通过课堂例题和课后作业进行对比归类，以期不再“物是人非眼迷离”.