回归经验模型调姿拓本溯源

☉湖南省常德市芷兰实验学校 陈金红

解题不仅是求解，更是思维过程的揭示；解题不仅是寻找答案，更需要的是“自觉分析”；解题分析不仅是数学学习的方法，更是一种理念；解题学习不仅是接受一种方法和思想，更是认识的补充、完善、提高与通俗化解读的过程.对一道初中背景的难题，尽管有些资料提供了思路，但分析粗糙复杂化了，为使初中生都搞得懂，本文就如何揭示、完善、通俗化再探如下.

题目：在两个三角形的六对元素（三对角与三对边）中，即使有五对元素对应相等，这两个三角形也未必全等.

⑴试给出一个这样的例子，画出简图，分别标出两个三角形的边长.

⑵为了把所有这样的反例都构造出来，试探求并给出构造反例的一般规律（要求过程完整，述理严密，结论明晰）.

再探 数学新课标把“双基”（基础知识、基本技能）变“四基”（基础知识、基本技能、基本思想、基本活动经验），其中把积累数学基本活动经验提到一个非常高的高度，是一种认识论的回归，因为活动经验确确实实在我们的工作中起到暗示、点拨的功效！

一、全等反例经验模型

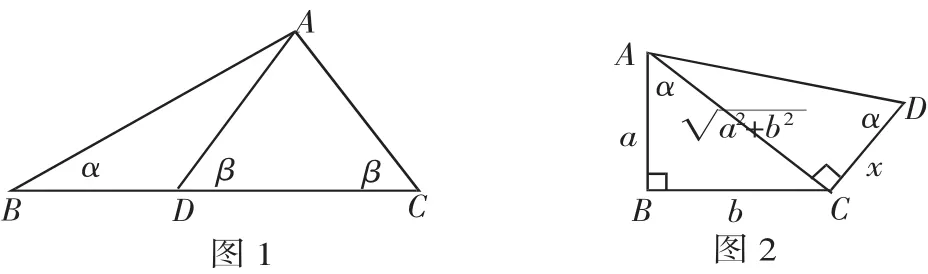
受原型“已知两边及一边的对角相等的两个三角形不一定全等”（简称SSA）启发：见图1，在△ABC与△ABD中，AD=AC、AB=AB、∠ABD=∠ABC，已经有三对元素对应相等了；再从角的添加入手：若能使∠BAD=∠ACB，那一定就有∠ADB=∠BAC了！从而好像有“五对元素对应相等，这两个三角形也不全等”！

但细看发现：由AD=AC⇒∠ADC=∠ACB=∠BAD⇒AB∥BC，出现矛盾！宣告尝试失败！

二、相似特殊经验模型

由上失败故转而分步使条件由少到多推进展开探究，退回到非全等的相似模型如图2，在Rt△ABC与Rt△ACD中，∠B=∠ACD=90°，∠BAC=∠ADC=α，此时这两个三角形相似了，于是有三个角、一条边（AC=AC）四个元素对应相等了，在此基础上只需再添一条边如BC=CD就符合要求了！

先由Rt△ABC∽Rt△DCA可得：

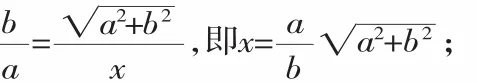
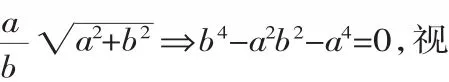
三、一般相似模型

由分析特殊相似模型得到启发，五个相等元素中不可有三边对应相等的条件，故从角元素入手、边由少到多推进的办法探讨一般相似模型：见图3，△ABC与△DEF中，已有三角对应相等.

四、一般线索的本质

从而有：∠A=∠D、∠B=∠E、∠C=∠F；AB=EF、BC=DF，但AC≠DE（m≠x）.

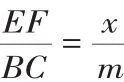
五、两个注脚

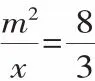
综合知：如果“五对元素（3对角元素、2对边元素）对应相等，这两个三角形也不全等”，那么这两个三角形必相似，并且每个三角形中较大边是其他两边的比例中项.

确实正如波利亚所言：没有任何问题是可以解决得十全十美的，总剩下些工作要做，经过充分的探讨与钻研，我们能够改进这个解答，而且在任何情况下，我们总能提高自己对这个解答的理解水平.当然在这个“节省解题力量、开发解题智慧”的过程中，我以为运用“回归经验模型，调姿拓本溯源”不失为一大良策！

1.黄玉华.在数学解题中试行波利亚“怎样解题表”的做法和体会.中学数学教学参考（初中）.2010年第1-2期.

2.陈金红.不要放弃更初等的想法.中学数学教学参考（初中）.2012年第1-2期.