优化递进式变式题组应用的几点思考
☉上海市华东师大一附中实验中学 刘海涛

刘海涛(生于1963年10月17日),上海市杨浦区人,任职于上海市华东师大一附中实验中学,2000年被评为中学高级教师,参加上海市市级课题《分层递进教学新法实践与研究》的研究,并先后在 《中小学数学》、《中学数学》《中国数学教育》《初中数学教与学》《数学教学》《上海中学数学》等专业期刊发表论文10多篇.主要从事初中数学课堂教学和初中数学分层递进教学的研究.
何谓递进式变式题组?递进式变式题组是指在课堂教学中,为了达到某一教学目的,根据学生的认知规律,合理有效地设计一组数学问题,且这组数学问题又有一定的内在逻辑联系,即前一个问题是后一个问题的特殊情况,后一个问题是前一个问题的一般的情况,这样由特殊到一般的题目组合称为递进式变式题组.这种递进式变式题组,层层递进,由浅入深,由简到繁,循序渐进,螺旋式上升,有利于学生对问题本质的深刻理解,进而掌握解题规律,突破教学中的难点;有利于学生巩固知识技能和提高学生的数学能力;有利于学生形成良好的数学认知结构.如果能恰到好处地使用递进式变式题组,就会使课堂教学取得事半功倍的效果,因此课堂教学中如何应用递进式变式题组,是值得每位数学教师常思考的问题.
一、突破难点建构数学认知结构
教学难点是指教师难教、学生难学的知识,或不易掌握的技能、技巧.难点有时又要根据学生的实际水平来定.在一般情况下,使大多数学生感到困难的内容就是难点,教师要利用各种有效策略加以突破,否则这部分内容不但学生掌握不好,还会给学生理解以后的新知识和掌握新技能造成困难.如何搭建合适的台阶突破难点,正是教学艺术之所在.要想攻克教学难点,极其重要的一条原则就是循序渐进,递进式变式题组较好地解决了上述问题.
例如:三元一次方程组的解法是初中代数教学难点之一,学生虽然已经知道了解法,用代入消元法或加减消元法把三元一次方程组转化为二元一次方程组,然后再通过消元把二元一次方程组转化为一元一次方程来解的思想方法.但因为方程和未知数较多,很多学生往往无从下手,因此在教学中通过编写递进式变式题组,由简单到复杂,然后使学生通过转化,再把复杂问题转化为简单问题,进而解出三元一次方程组,效果会更好.
在消元的方法选择上,要求学生除特殊的三元一次方程组(至少有一个方程是一元一次方程)选用代入消元法外,对非特殊三元一次方程组,选用加减消元法,因为代入消元法的运算量比较大,学生运算容易出错.在加减消元法中,学生对加法运算出错率低,因此笔者在教学中,主要把解三元一次方程组的重点放在了用加法消元上,运用如下递进式变式题组进行教学.
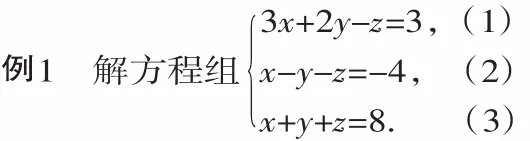
方程组中未知数的系数特点,一个方程的未知数z的系数与另外两个方程中未知数z的系数是互为相反数,因此用加法就能消去未知数z,把方程组转化为二元一次方程组.
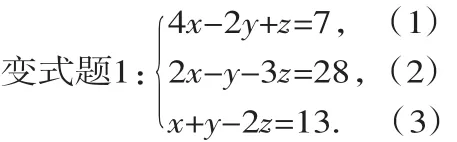
观察方程组中未知数系数特点,不存在一个未知数的系数与另外两个方程中同一未知数系数是互为相反数,但是把方程(3)乘以2就可与(1)相加消去y,再(2)+(3)消去y,从而通过两次相加,消去未知数y,把三元一次方程组转化为二元一次方程组.
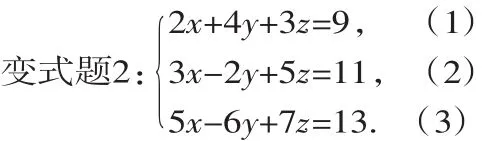
观察方程组中方程未知数系数特点,不存在有未知数的系数是互为相反数的,这时通过观察方程组中未知数系数的特点,首先把方程(1)乘以3,方程(2)乘以6,方程(3)乘以2,把方程组转化为例题的类型,从而使问题得到解决,也可以把(2)乘以2,把方程组转化成变式题(1)的类型,再解.
三道题不是简单的重复,彼此之间有密切的联系,前一个问题是后一个问题的特殊情况,后一个问题可转化成前一个问题类型进行解决,这样的递进式变式题组能与学生的数学认知结构相联系,前一个问题解决后,在此基础上进行新的建构,学生的数学认知结构经历了从简单到复杂不断扩充的过程,符合学生认知规律,从而使学生能够很好地掌握三元一次方程组的解法.
二、探究规律建构数学认知结构
规律是事物发展过程中本身所固有的必然联系.规律是客观存在的,是不以人们的意志为转移的,人们只能发现规律,利用规律,不能改变规律.苏霍姆林斯基说“人的内心里有一种根深蒂固的需要,总想感到自己是发现者、研究者、探寻者”.数学教学中有很多规律需要学生去探究,教学中要鼓励学生去探究规律并掌握规律,教师要为学生的学习创设探究情境,建立探究的氛围,促进探究的开展,把握探究的深度,这样才能调动学生探究的积极性,激活学生探究的潜能,以寻到规律.
例如:同底数幂乘法法则的探究过程,给出如下递进式变式题组,以使学生自主探究规律.
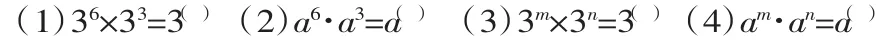
显然(1)是底数、指数都是具体数,学生很容易利用乘方的意义得到问题的答案.接下来(2)(3),在(1)的基础上,(2)把底数由具体数变成了字母,(3)把指数由具体数变成了字母.(4)是在(2)(3)的基础上,把底数、指数都变成了字母,得到了一个一般的同底数幂乘法的规律.在以上探究过程中,充分运用递进式变式题组,由特殊到一般地进行探究,使学生跳一跳就能摘到果子,从而使学生能够顺利地得到乘法法则,同时建构数学认知结构.
三、搭“引桥”建构数学认知结构
数学教学中,很多新知识的学习,往往不能和学生的数学认知结构直接相联系.教师在教学新知识时,如果直接把新知识呈现在学生面前,学生要改组原有的数学认知结构,顺应新知识的学习,产生新的数学认知结构,这样给学生的学习带来一定的困难,学生很难理解,不符合学生的认知规律.因此教学中要充分利用递进式变式题组,小步走,螺旋式上升,从简单的问题入手,通过递进式变式,最后解决问题的一般情况,从而总结出问题的一般规律.这样能够使学生原来以顺应为主建构数学认知结构,转化为以同化为主建构数学认知结构,从而使学生能够顺利地掌握新知识.
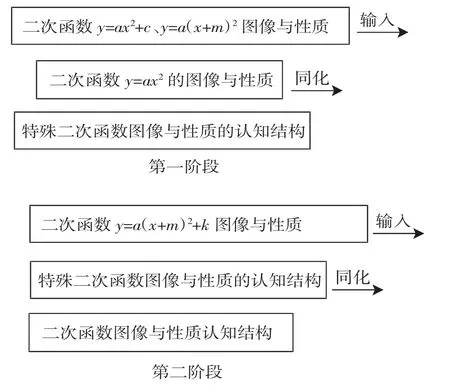
例如:在学习二次函数的图像与性质时,我们首先研究的是特殊类型二次函数y=ax2的图像和性质.显然这个函数的图像与性质与学生原有的数学认知结构距离很小,学生学习起来比较容易,学生也很容易利用描点法画出这类二次函数的图像,进而通过总结得到这类二次函数的图像和性质.在此基础上我们又研究了y=ax2+c类二次函数的图像和性质,显然y=ax2是y=ax2+c的特殊情况,y=ax2+c是y=ax2的进一步推广,通过研究得到了y=ax2+c图像与性质,同时得到了二次函数y=ax2+c与y=ax2两种类型图像的关系.在此基础上,我们又研究了y=a(x+m)2类型二次函数的图像与性质,显然这种类型二次函数是y=ax2的推广,通过对比得到二次函数y=a(x+m)2的图像和性质,以及与二次函数是y=ax2的图像的关系.最后研究一般二次函数y=ax2+bx+c的图像和性质,通过把二次函数配方转化为y=a(x+m)2+k的形式,再把二次函数y=ax2+c与y=a(x+m)2组合得到一般二次函数y=ax2+bx+c的图像与性质.
以上显然是由简单到复杂的一个递进式变化过程,通过y=ax2图像与性质入手,最后得到一般二次函数的图像与性质.在数学教学的过程中,有些知识与学生的原有的数学认知结构有一定的跨度,这时,教师在教学设计上,利用搭引桥的策略,才能使学生一步一个台阶,把新知识同化到原有的数学认知结构中去,认知过程如下.
四、构造问题链建构数学认知结构
问题链是指问题与问题的精心连接与递进.它将问题像“链条”一样串联起来,环环紧扣,层层递进.能覆盖重要的知识点、基本题型、重要的解题思路.教学中随着“问题链”的逐一呈现,学生在不知不觉中既解决了问题,又获得了知识,又提高了数学思维能力.
例2 求证:顺次连接平行四边形各边中点所得的四边形是平行四边形.
变式1.求证:顺次连接矩形各边中点所得的四边形是菱形.
变式2.求证:顺次连接菱形各边中点所得的四边形是矩形.
变式3.求证:顺次连接正方形各边中点所得的四边形是正方形.
通过这样一系列变式训练,一是使学生充分掌握了四边形这一章节所有基础知识和基本概念,强化沟通了常见特殊四边形的性质定理、判定定理、三角形中位线定理等,最大限度地拓展了学生的解题思路,激活了学生的思维,激发了兴趣.二是能够使学生懂其原理,知其方法,通其变化,形成此类命题的命题域与命题系,进而使学生形成良好的CPFS结构,而研究表明,良好的CPFS结构是一种优良的数学认知结构,因此有利于学生建立良好的数学认知结构.
总之,在教学过程中要针对教学内容的特点,优化应用递进式变式题组,才能达到非常理想的教学效果.另外对递进式变式题组的设计,要依据学生的数学认知结构和认知发展水平,从学生的生活经验和已有的知识背景出发,巧妙设计,才能创设最佳的认知情境,才能让学生利用已有的知识结构来同化新知识,实现知识的迁移,从而提高递进式变式题组应用的有效性.
1.刘海涛.初中数学教学中变式题的应用技巧[J].上海市:上海中学数学.2011(5).
2.曹一鸣,张春生主编.数学教学论.北京市:北京师范大学出版社[M].2010(8).
3.张英伯,曹一鸣,丛书主编,喻平编著.数学教学心理学.北京市:北京师范大学出版社[M].2010(1).

