地方坐标系的建立

杨井辉

(中石油工程设计有限公司青海分公司，甘肃敦煌 736202)

0 引言

工程测量在建立测区控制网时，按国家相关规范规定，应尽量采用国家统一标准高斯坐标，但由于高海拔地区采用标准高斯坐标，长度投影变形超过允许范围。为了满足图上长度和经坐标反算长度与实际地面长度相一致(即满足规范要求)，可以采用合适的投影基准面以控制长度变形。此方法也可称为地方坐标系。为了限制变形，本文采用∑ΔSi=min的方法获取合适的高程抵偿面。

1 抵偿投影面的选择

2)椭球面上的长度投影到高斯面上时产生的长度变形，取其主项有:

长度变形来源于以下两个方面:

1)将实地长度换算到椭球面上时产生的变形，取其主项有:

其中，ym为归算边两端点横坐标自然值的平均值;Hm为归算边高出参考椭球面平均高程;Rm为参考椭球面的平均曲率半径。

在不影响推证严密性的前提下取Rm=RA=6 371 km，Sm=S。于是综合变形有:

由于式(3)中有两个不存在具有实际意义的自由极值变量，所以无法获得ΔSi。现采用∑ΔSi=min的方法来确定抵偿投影面。首先要确定ym∈(ymin，ymax)的值，再根据ym来确定Hm。

设ym为定值，则有:

将式(4)代入式(3)中可得:

式(5)中yi为第i段归算边两端点横坐标自然值的平均值。

由于yi在(ymin，ymax)上连续可得:

由∑ΔSi=min可得:

将式(8)代入式(4)可得:

从而可得抵偿高程投影面的大地高为:H′=H－Hm，其中，H为测区的平均高程。

2 算例分析

为了了解此方法的综合投影变形的特点，本文采用与文献[4]中的例子相比较加以说明。设测区的平均高程H=2 000 m，Sm=S=1 000 m。现取两种情况分别说明:

1)测区位于中央子午线一侧，设测区y∈(40 km，100 km)。

2)测区跨越中央子午线，设y∈(－20 km，100 km)。

将两种情况的y值分别代入式(8)和式(9)中可得到两种不同方法的ym值、Hm值和∑ΔSi值。

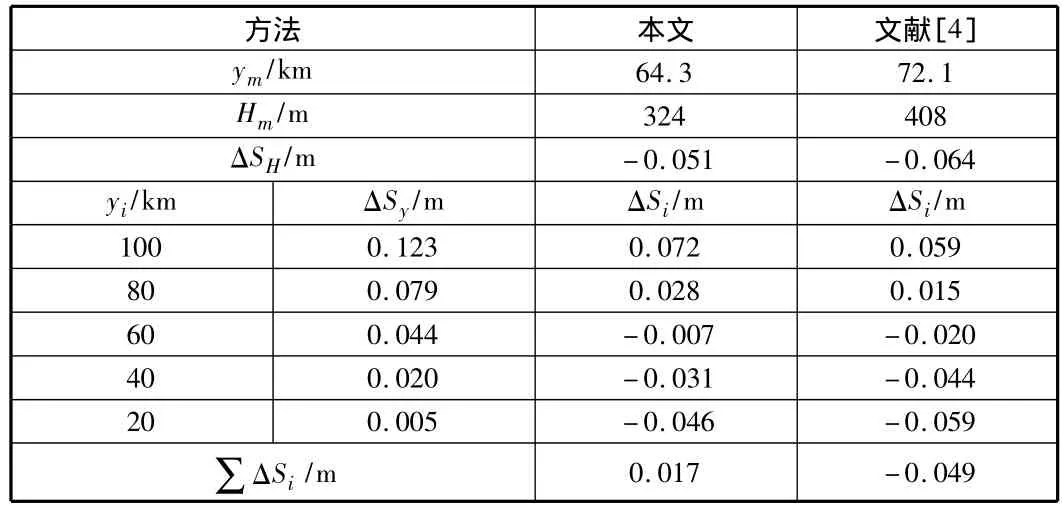
表1 y∈(40 km，100 km)时的ym值，Hm值和∑ΔSi值

表2 y∈(－20 km，100 km)时的ym值，Hm值和∑ΔSi值

具体比较见表1，表2。

从表1，表2的结果能够看出本方法能有效的抑制测区的整体变形但局部区域还存在变形过大。每一种方法都有其自身的局限性，为了能使测区变形达到规范要求，我们还可以采用高程抵偿的任意带高斯投影。若还不能满足规范要求，则应考虑分带或(和)分层进行投影。由于具体工作情况的不同，工程测量人员应结合具体工作的实际情况采用最佳的方法。

[1]田青文，刘万林.控制测量学[M].西安:西安地图出版社，2004:160-164.

[2]张 勤，李家权.GPS测量原理及应用[M].北京:科技出版社，2005:180-182.

[3]孔祥元，郭际明.控制测量学(下)[M].武汉:武汉大学出版社，2006:124-127.

[4]范一中，王继刚，赵丽华.抵偿投影面的最佳选取问题[J].测绘通报，2000(2):98-99.

[5]王继刚，王 坚，于先文.具有抵偿面的任意带高斯投影直角坐标系的选取方法[J].测绘通报，2002(11):43-44.