基于复杂网络的社交网站用户评价模型研究

徐翔斌，涂 欢 ，王佳强

（1.华东交通大学机电工程学院，江西南昌330013；2.中南大学交通运输工程学院，湖南长沙410075）

SNS（social network site，社交网站），指帮助人们建立社会性网络的互联网应用服务，而近来异常火爆的微博也是属于SNS的一种。已有学者对SNS商业价值进行了较为深入的研究，王璐[1]提出了SNS的4种网络营销模式，口碑营销、植入式营销、病毒式营销和邀请营销，并对SNS网络营销的前景进行了展望。邢相军，贾元斌等[2]则指出SNS除了其在广告，增值服务和网页游戏等方式外，电子商务与SNS的联姻更能体现它的价值，并探讨了SNS模式特点下的电子商务网站的发展。连环[3]指出，SNS的社会性、开放性、互动性等特征使其在企业信息化建设中具有重要的作用，在探讨企业实体所涉及关系的基础上，阐述SNS在企业内部知识管理、客户关系管理以及企业精准营销等方面的应用，为企业的信息化建设提供指导意义。

但到目前为止，对SNS客户进行价值评估研究不多，更没有利用复杂网络理论。本文在相关研究的基础上，以微博为例，利用复杂网络，客户关系管理、市场营销等理论，建立一套完整的微博客户价值评价体系和用户价值评价模型。

1 基于复杂网络理论的微博客户评价模型

1.1 微博和复杂网络

复杂网络不同于完全规则网络和完全随机网络，具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络[4-5]。微博用户网络作为SNS的一种也属于复杂网络。它是基于WEB2.0平台新近兴起的一类开放互联网社交服务。它与传统的社交网站（social network sites）一样都是基于“六度分割”的概念[6]。此概念是指任意两个陌生人都可以通过人际关系找到对方从而使每个人的社交范围可以不断扩大。微博让用户之间形成一张无形的大型社会化网络，该网络中的节点代表用户，边表示用户之间的相互联系。当处在该网络中某一个用户产生一个动作，就会传递到网络中与之关联的其他用户。如果其他用户有所反应，同样会不断扩散到与该用户关联的其他用户。如此下去，就会不断扩散到整个网络，永无休止地进行传播，从而形成一种“蝴蝶效应”。

微博这种用户关系和信息传播作为一种新的信息渠道，为客户关系管理提供了新的思路和方向。虽然微博具有用户信息真实、用户定位清晰、用户关系网络化、用户黏性强等特点，然而其用户关系具有隐蔽性、关联性、动态性、瞬时性和涌现性等特征，与传统的客户关系有很大的不同。以客户获取为例[7]，获取微博中的关键客户即可获取该网络中与之关联的其他客户，而传统的客户关系管理则需要逐个获取客户，如图1、图2所示，可见传统的客户关系管理理论和方法在这里遭遇到瓶颈。

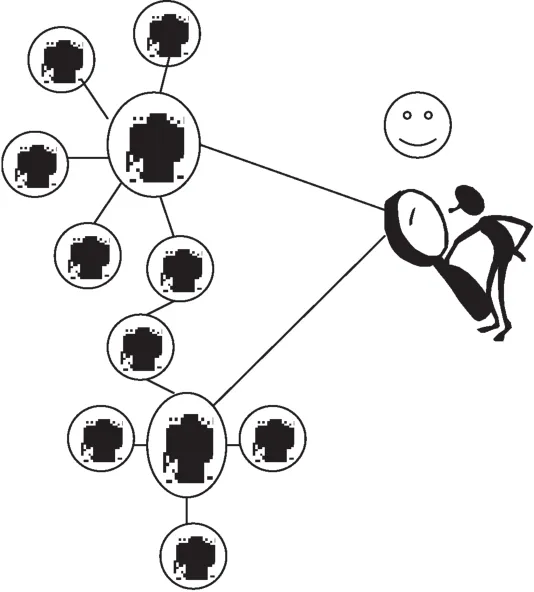
图1 微博客户获取Fig.1 Microblog customer acquisition

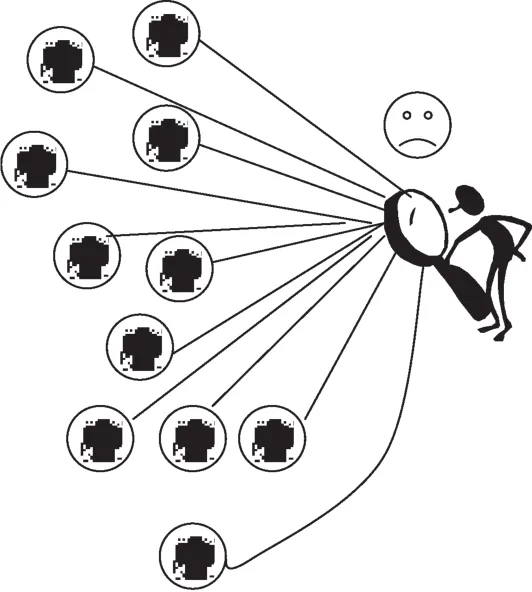
图2 传统客户获取Fig.2 Traditional customer acquisition

本文运用复杂网络理论来对微博用户网络进行评价分析，并致力建立一个微博用户的客户价值模型。下面首先介绍下复杂网络中重要的客户评价指标。

1.2 微博客户评价指标

微博用户网络节点数量庞大，节点之间关系明确，每个用户代表网络中的一个节点，边代表用户之间的关系。

1）度指标。度指标（degree centrality）用于描述在静态网络中节点所产生的直接影响力，其值为与该节点直接相连的节点数。对于加权网络，一个节点的度D(i)是与它的边缘时间相应的所有价值的总和。在这两种情况下，其数学表达式如公式（1）所示

其中：g是指网络节点的最大值；Xij表示节点i到节点 j的度。度指标定义表明节点与其他节点直接通讯能力的越强，其重要性越强。它适合研究节点的直接影响力，但只能测试网络没有重复链接的情况。

2）紧密度指标。紧密度指标（closeness centrality）用于刻画网络中的节点通过网络到达网络中其他节点的难易程度，其值C(i)定义为该节点到达所有其他节点的距离之和的倒数。其数学表达式如公式（2）所示

其中：g是指网络节点的最大值；δij是指节点i到节点 j的最短距离。紧密度指标考虑了节点间通讯的独立性，即与其他节点通讯的可能性对通讯所需中间媒介的最少个数的依赖程度。它可以用于研究信息在最短路径中传播及信息并行复制的情况，它的链路只会被使用一次，且易于在最短路径上向整个网络扩散。

3）介数指标。介数指标（betweenness centrality）刻画了网络中的节点对于信息流动的影响力。其数学表达式B(i)如公式（3）所示其中：gjk(i)表示节点 j和节点k之间的最短路径数；gjk(i)表示节点 j和节点k之间经过节点i的最短路径数。介数指标是用于刻画动态网络中节点被经过的次数，所以它可以用于信息在最短径中传播及信息连续复制的情况[8-9]。

2 基于复杂网络理论的微博客户评价建模

单一化的评价指标往往存在它的不确定性，为了更加合理地评价微博客户价值，度指标、紧密度指标和介数指标这3项参数往往结合起来使用，在这里，我们就同时利用以上3个指标来进行客户评价。

1）计算客户的度指标，在微博客户网络中，度指标能最直接的体现客户对网络中其他客户的直接影响力。

2）计算客户的紧密度指标，在微博客户网络中，紧密度指标体现了客户通过整个网络对其他客户的间接影响的能力。

3）计算客户的介数指标，在微博客户网络中，介数指标体现了客户对整个网络中信息流动的影响力。

如果网络中的一个客户同时具备较大的度指标、紧密度指标以及介数指标，则该客户在网络中必然具有较大的影响。相应的，该客户就是客户关系中的关键客户。

为了用数学语言描述出网络中节点的价值，本文建立的了一个数学模型。

设网络中共有n个客户，分别用x,y,z来表示每个客户i的度、紧密度和介数指标。则网络中客户的平均度、平均介数和平均紧密度指标则分别为

则客户i的价值指数如公式（4）所示

式中：α,β,γ分别表示客户对其他客户的直接影响力、客户对其他客户的间接影响力和对网络信息流动影响力在评价客户价值中所占的权重。

本文在评价客户价值时，同时考虑度、紧密度和介数指标进行综合评价，并认为在评价过程中这3个指标所占的权重是同等重要的。故可以认为α=β=γ，且另他们的值为1，则最后客户i的价值指数Qi如公式（5）所示

式（5）即为评价客户价值的数学表达式。本文从新浪微博上采集了部分数据，并利用该数学模型对所采集数据进行分析。

3 数据分析

3.1 微博数据采集和预处理

本文的数据都来源于新浪微博，由于微博用户数量巨大，只能对其进行采样。采用的方法是雪球抽样[10]。具体实施是，先选择微博中单一的用户，然后就是该用户所有的关注对象和粉丝被选取，接着所有被选取用户的关注对象和粉丝再被选取。这个过程一直持续到抽样的用户数量满足要求为止。这些在第n次被选取的用户集合被称为第n层，n同时也就是自中心网络的半径。由于关键用户（有很多链接的用户）的高关联度，这种滚雪球抽样方法将能在很短时间内获得这些关键用户。因此，初始用户是否是关键用户不会再描述这个抽样的网络时产生显著差异，同时也保证了所采集到的数据能够反映总体微博网络的特点。

本文设计了专门采集微博用户数据的网络蜘蛛，采集起止时间为2011年8月8日至2011年8月19日，共计12天，总共采集到的数据中包含52 990个用户和1 109 826条表示个用户间关系的边，共同构成了一个庞大的网络。

本文利用Pajek软件来对搜集到的数据进行分析，Pajek软件是可以处理结点数大于100万的大型网络，同时具有网络分析和可视化功能的软件。在数据分析前，先对数据进行些处理，在搜集到的用户数据中，有部分用户是属于不活跃用户，甚至是“僵尸”用户，这些用户注册了账号后，长时间没有任何动作，把近3个月内没有任何动静的用户剥离出来，经过筛选，总共有1 210个“僵尸”用户，去除掉这些用户后，得到的新数据总共包含51 780个用户节点。需要说明的是，这些“僵尸”用户基本都处于复杂网络的最边缘，且这些用户的关注对象和粉丝数量都非常少，即网络中它与其他节点之间的有向边的数量都很少。所以，不用担心去除这些用户后对这个网络的完整性造成影响。

3.2 微博基本特征分析

1）平均路径长度。平均路径长度（average path length，APL），经过计算，该网络的APL为4.123。也就是说该网络中任意两个用户之间的平均距离只有4.123。可以看到，这一数值大大低于完全随机网络。而APL小于6，也符合六度分离理论。这表明该网络传递信息的能力非常强。

2）集聚系数。集聚系数（clustering coefficient），经过计算，该网络的集聚系数为0.169。而这一数值要比完全随即网络中的集聚系数要大的多，这说明了该网络中的“物以类聚，人以群分”的特点。

3）度指标。该网络中总共包含51 780个用户，而经过计算各节点总度总数为1 097 736。每个用户的平均度为21.2。而统计结果表明，在该网络中，用户度小于20的用户占据节点总数的76%，而用户度大于100的用户占总用户数的不到5%。因此，该网络中只有少数用户拥有较大的度数，大部分用户的度数都较小，且度分布服从幂律分布。

经过对以上3个指标的分析，发现该网络有着较短的平均路径长度和较大的集聚系数，度分布函数符合幂律分布，表明微博属于典型的无尺度复杂网络。

3.3 微博客户评价

利用式（5）可以计算微博网络中每个客户的价值系数，这是在认为α=β=γ的情况下得到的结果。但在实际情况下，面对不同的产品、不同的客户α，β，γ的取值也会随之浮动。

而在目前一些企业在利用微博进行产品宣传时，都是盲目的找一些粉丝数量大的名人来进行宣传，但大部分时候，这种策略往往并不是最优效果的。这是由于整个网络中存在着“富人俱乐部特性”和“异配性”。这在我们所采集的数据当中也体现的很明显，下面就根据所采集的数据来说明这两个特性，对企业利用微博进行产品营销和客户关系管理时所造成的影响。

所谓“富人俱乐部”特性，是指网络中少量的节点具有大量的边，这些节点也称为“富节点（rich nodes）”[11]，它们倾向于彼此之间相互连接，构成“富人俱乐部（rich-club）”。从采集的数据来看，也恰恰如此，网络中度指标大于100的节点寥寥无几，而这些节点之间却又连接紧密，虽然这些“富节点”掌握着大量的粉丝，但并不意味着，这些富节点就掌握了网络中的“话语权”。这是由于“异配性”[12]的存在，即一个节点的度越高，其邻居的平均度越低，从采集数据也能验证这一点，那些节点度最大的点的邻居节点的度大大低于整个网络的平均度。可见这种盲目的策略是很难达到预期的效果的，下面就面对不同产品、不同的客户是采取何种对应策略，α，β，γ权重的取值提出建议。

策略1：当目标客户群非常明确时，则主要看中度指标，即α取更大的值，例如要在微博网络中进行数码产品的推广，那么我们主要找到那些粉丝最多的数码类产品微博，即度指标最高的用户，而此时紧密度和介数指标相对不太重要。

策略2：紧密度主要是决定信息在网络中传递的速度，因为紧密度越高的点，信息能在网络中实现并行复制，所以他的速度是最快的。当企业的某种新产品上市，而其产品相对于竞争对手的同类产品的差异化不大，即容易被其他产品替代时，为了迅速扩大产品影响，获得口碑，那么产品信息的传播速度此时是最重要的，则主要看中紧密度指标，即β取更大的值，而此时度指标和介数指标相对不太重要。

策略3：介数指标主要决定信息在网络中传播的广度，介数指标越高的点，网络中信息经过该点的几率越大，所以介数越高的点，越有利于信息传播的范围更广。当企业的某种产品具备足够强的竞争力，市场上无其他同类产品对其构成威胁，此时，企业的宣传策略就是要让更多的用户知道他的产品，则主要看中介数指标，即γ取更大的值，而此时度指标和紧密度指标相对不太重要。

建立以上客户价值评价模型的意义在于可以指导企业在利用微博进行产品营销和客户关系管理时，针对不同类型的产品，有的放矢，选择正确的策略、适当的客户，这可以大大提高企业的效率和降低企业的成本。

4 总结和展望

本文利用复杂网络理论对微博客户网络进行了分析，并通过设计网络蜘蛛抓取新浪微博系统的用户数据，通过建模和数据分析后得到以下结论。

1）微博用户网络具有较短的平均路径长度，较大的聚集系数和度分布服从幂率分布等典型的复杂网络特征。

2）建立了基于度、介数及紧密度指标的微博客户价值综合评价模型。

3）提出了在企业在实施微博营销，针对不同产品，不同的客户差异化运营策略。

本文的研究结论可以为企业实施基于类似微博的网络营销提供决策指导和运营参考。

本文仅对微博用户价值评价进行了初步的实证研究，但对微博客户关系的动态演化及其动力学特征并未涉及，并未考虑用户的发言数量和活跃程度，而这也是研究微博客户关系的关键之一，今后的研究可以就此展开。

[1]王璐.浅谈基于SNS的网络营销[J].经贸论坛，2010，7（8）：83-84.

[2]邢相军，贾元斌.SNS模式下的电子商务网站发展探索[J].生产力研究，2010，8（2）：115-116.

[3]连环.SNS在企业信息化中的应用研究[J].应用研究，2010，4（1）：63-65.

[4]ALBERTLASZLO BARABASI，EEIC BONABEAU.Scale-free networks[J].ScientificAmerican，2003，288（5）：50-59.

[5]WATTS DJ，STROGATZ SH.Collective dynamics of‘small-world’networks[J].Nature，1998，393（6）：440-442.

[6]MILGRAM S.The small world problem[J].Psychol Today，1967（6）：62-67.

[7]段楠楠.电子商务企业客户关系的预测与动态管理[J].华东交通大学学报，2010，27（1）：119-124.

[8]王林，戴冠中.复杂网络的Scale-free性、Scale-free现象及其控制[M].北京：科学出版社，2009：107-111.

[9]汪小帆，李翔，陈关荣.复杂网络理论及其应用[M].北京：清华大学出版社，2006：55-56.

[10] SANG HOON LEE，PANJUN KIM，HAWOONG JEONG.Statistical properties of sampled networks[J].Physical Review，2006，273（1）：1-7.

[11]ZHOU S，MONDRAGON R J.The rich-club phenomenon in the Internet topology[J].IEEE Communication Letters，2004，8（3）：180-182.

[12]ZHOU S，MONDRAGON R J.Accurately modeling the Internet topology[J].Phys Rev E，2004，7（6）：104-108.