运行条件下输电线路载荷能力定值

王艳玲，韩学山，孔令元，梁立凯，4，周晓峰

（1.山东大学电气工程学院，济南 250061；2.威海职业学院机电工程系，威海 264210；3.山东电力集团公司枣庄供电公司，枣庄 277100；4.山东大学机电与信息工程学院，威海 264200）

对于一个大型电力系统，其电网输送有功功率的能力对于整个系统运行的安全可靠性有着很大的影响。经济、环保及土地使用等诸多因素促使现代电力系统的运行越来越接近其最大能力的边缘，对输电网的输电能力进行研究已经成为目前研究的热点问题。然而电网的输电能力主要取决于电网中关键输电线路的载荷能力［1］，所以对交流输电线路的载荷能力进行实时定值具有很重要的意义。

一直以来，交流输电线路载荷能力评估采用st.clair曲线［2］，该曲线由st.clair根据实验数据绘制，当时主要反映345kV及以下电压等级输电线路载荷能力与输送距离间的关系。随后文献［3］，通过线路两端系统分别进行戴维南等值，给出st.clair曲线的分析计算模型，指出输电线路的输电能力受3种因素限制，分别是热、电压和稳定限制。在该等值模型中，戴维南等值电势是给定的，等值电抗由线路首末端三相短路容量估计，忽略电阻影响。文献［4］给出了具体的一条输电线路在特定的系统运行环境下输送能力的计算方法，在此计算方法中，同样对送、受端系统进行了戴维南等值，等值电抗求取同文献［3］，但戴维南等值电势是通过一次潮流计算得出的，考虑其变化。在国内，柴旭峥等［5，6］在分析交流输电线路实际运行特性及我国相关导则对输电线路电压和无功具体要求的基础上，提出了更适合我国的交流输电线路输送能力曲线计算的改进算法。在以上的计算方法中，均通过对送、受端系统进行独立的戴维南等值来求取线路的载荷能力，而且在线路的载荷能力增加的过程中，戴维南等值参数均保持恒定。这就使求解的能力限定在设计环境下，而不是运行环境下，因为电网随运行模式变化的戴维南等值参数不是固定不变的，它们依赖于电网拓扑、发电状况、负荷模式和无功电源状况等因素，随着输电线路载荷能力的增加，系统各节点的注入以及各节点的电压、相角等状态量都是变化的，由此送、受端系统的戴维南等值参数也应该是变化的，而不是保持为恒定值。2001年，刘天琪等［7］提出了交直流联络线局部控制的变参数等值模型，在此变参数等值模型中戴维南等值参数随运行环境的变化而变化，但模型中联络线两端局限在连接两个相互独立的系统，无法考虑并行流问题。因高压及超高压电网中环网的存在，仅通过对被研究输电线路送、受端的戴维南等值来研究载荷能力，难以考虑并行流影响，必然影响定值精度。

为此，本文针对上述问题建立基于扩展潮流的送受端系统双端口诺顿等值模型，并将其化简为双端电源等值形式，基于状态估计，实现在线跟踪双端电源等值电势，并推算出等值电势的变化趋势，进而实现输电线路载荷能力在线定值，本文所提等值模型适应环网结构，体现了互联系统中并行流对输电线路载荷能力的影响，而且通过等值参数的变化反映出系统的非线性及时变性。在算例中以IEEE39节点系统为例，通过连续潮流验证了该模型和算法的可行性及有效性，并对威海电网220 kV线路进行了典型日载荷能力在线定值计算和分析。

1 问题描述

1.1 输电线路模型

本文用于定值分析的输电线路模型如图1所示，其中忽略电阻影响。图1中，Z0为波阻抗；β为相位常数；l为输电线路长度；˙Us和˙Ur分别为输电线路送受端的母线电压；˙Is和˙Ir分别为线路首末端的注入电流；Bs、Br和Xs反映输电线路的并联和串联补偿对应的参数。根据图1，由电工原理推得

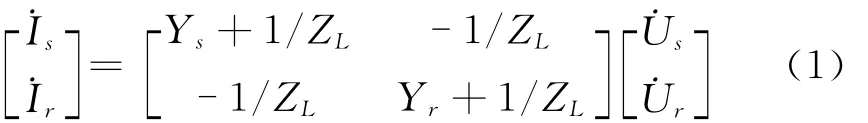
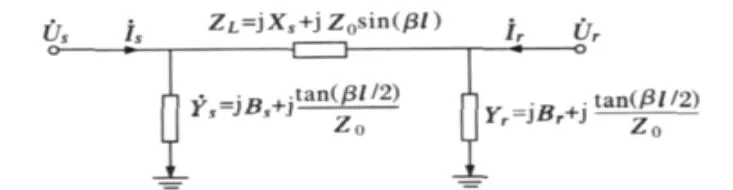
图1 输电线路等值模型Fig.1 Equivalent model of tuansmission line

1.2 扩展潮流的双端口诺顿等值

为反映从输电线路送（受）端端口看进去时端口注入电流与送（受）端系统输出电压间的关系，本文在运行点处对送受端系统进行等值处理，并通过网络化简获得送受端系统的基于扩展潮流的双端口诺顿等值模型，以下是具体推导过程。

送受端系统的电网节点电压方程为

式中：t为送受端系统内电源节点集合；s为输电线路送端端口所在节点；r为输电线路受端端口所在节点；e为其他节点组成的集合；It为节点集的注入电流列向量；˙Is和˙Ir既是系统在输电线路送受端端口的输出电流，也是系统向输电线路首末端的注入电流。

分析中，打破电源节点端电压不变（PV节点）的假设，采用扩展潮流模型，即对发电机采用电压源带内电抗模型，则电源在端口处的输出电流和端口电压之间可统一表示为

式中：Et0为发电机内电势；Xteq为由发电机内电抗形成的对角阵。将式（3）代入式（2）并化简可得

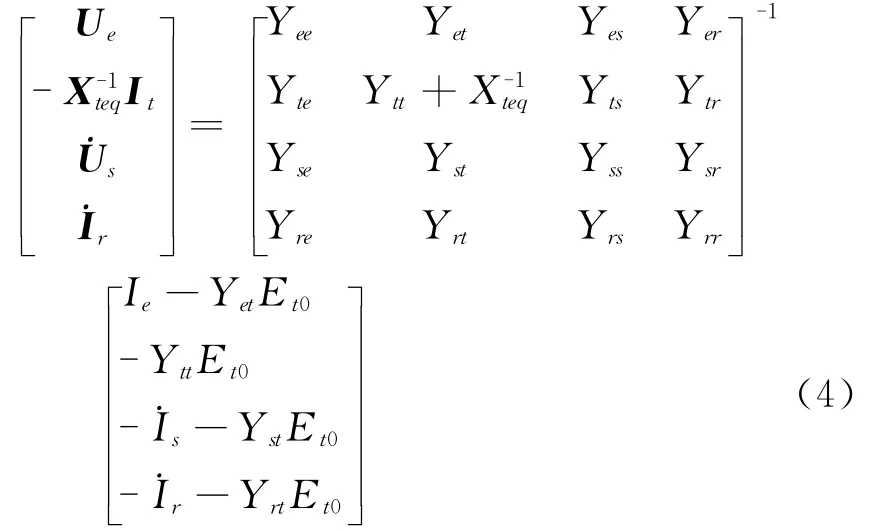
若令

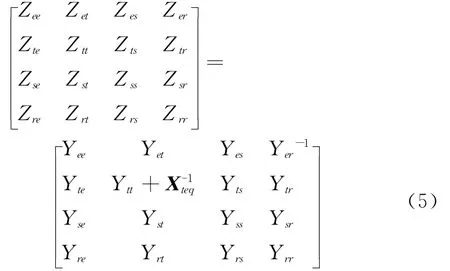
则代入式（4）可得

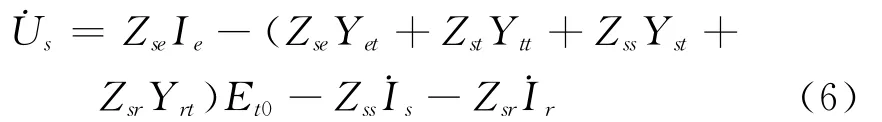
由此，输电线路送端端口电压和注入电流间满足

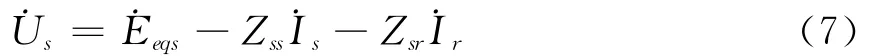
其中

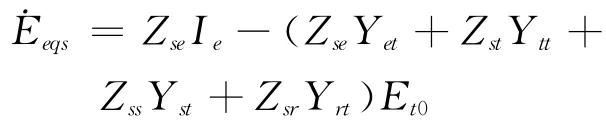
由式（7）可见，系统送端端口电压不仅受到送端端口注入电流影响，还受受端端口注入电流的影响，这主要是由送受端间与并行通路引起的。

对输电线路受端端口，同理有

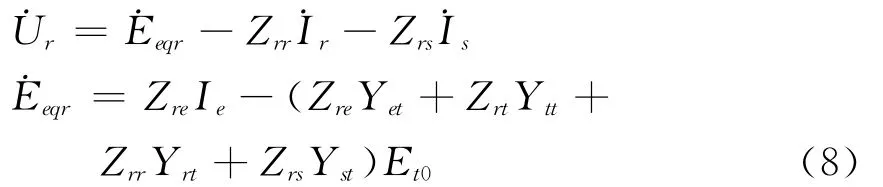
式（7）与式（8）可表述为双端口戴维南方程为

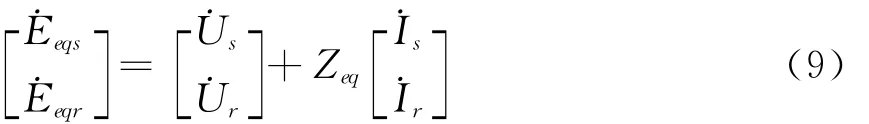
其中

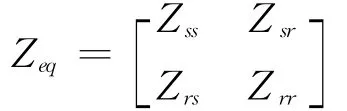
将式（9）等号两端乘以Z－1eq，将其转化成双端口诺顿方程可得

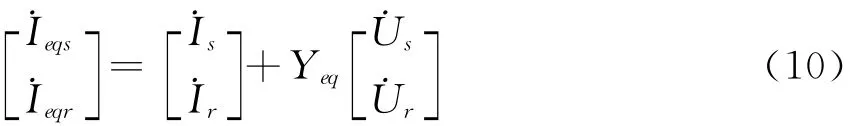
其中

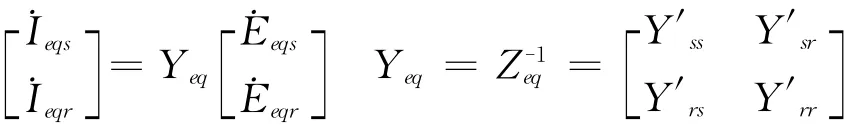
根据两端口网络的基本理论和节点导纳矩阵的物理意义，对式（10）等值方程用Π型等值电路来模拟，由此可得送受端系统的双端口Π型等值电路，如图2所示。在图2的基础上结合输电线路的Π型等值电路（图1），可得系统的等值模型如图3所示，化简图3可得输电线路在线定值计算双端电源等值模型如图4所示。图4中：

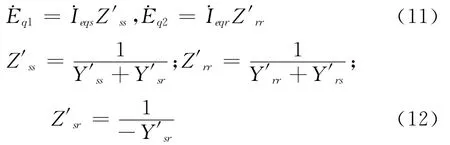
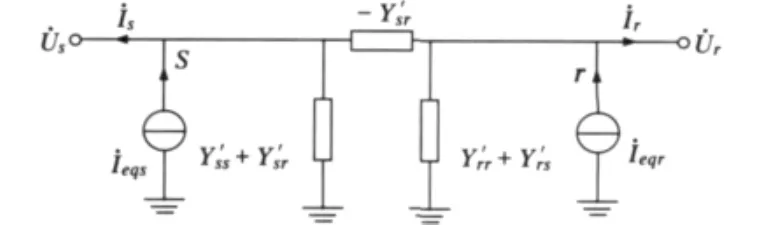
图2 送受端系统的Π型双端口诺顿等值模型Fig.2 Dual－port NortonΠ－type model of sending and receving end systems

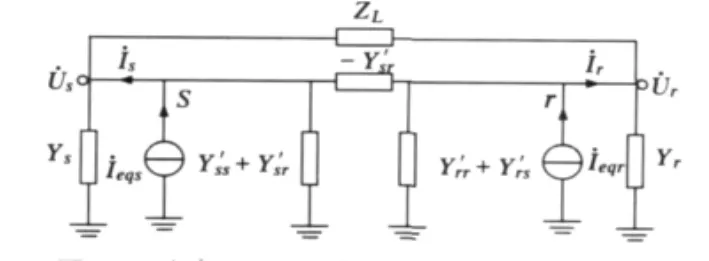
图3 结合Π型输电线路的系统等值模型Fig.3 Equivalent model of system combining withΠ－type model of transmission line

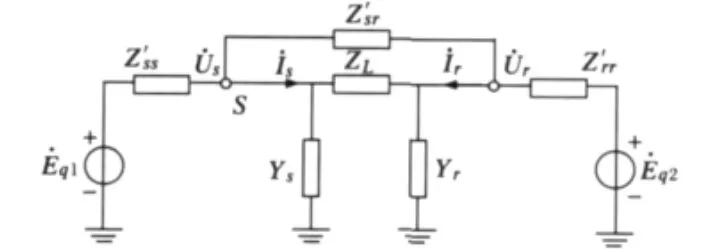
图4 输电线路载荷能力在线定值模型Fig.4 Equivalent model for online valuing loadability of tuansmission line

图4中等值阻抗Z′ss和Z′rr反映随输电线路载流变化系统对输电线路送受端节点电压的支撑能力。等值阻抗Z′sr的存在表征了送受端系统中与被研究输电线路并行的支路的存在及其分流作用。送受端系统双端电源等值电势˙Eq1、˙Eq2，反映了当前时段的系统电压水平。

特别的，当送受端系统相互独立仅以所分析输电线路连通时，可对送端和受端系统分别进行予以上述类似的推导，得到线性化后的送端和受端系统等值模型如下：

此时对应定值计算模型中Z′sr＝0，系统等值模型就是送受端系统的单端口戴维南等值模型，这与文献［5］的计算模型保持一致。

2 输电线路载流量在线定值分析

2.1 等值参数在线跟踪的实现

线路载荷能力在线定值所需的实时数据源来自电网状态估计。状态估计每执行一次，就可以提供一次电网拓扑结构、电压水平、负荷有功和发电分配的实时信息。借此可通过式（11）和式（12）计算系统等值模型参数。然而，对于大规模电网这种方法的计算量较大，这不利于在线定值快速计算。可见，快速简洁的系统等值参数估计方法是实现输电线路载荷能力在线定值的关键。

就在线跟踪戴维南等值参数，有关文献对其进行了研究［8～10］，这些研究都是为了进行电力系统的在线电压稳定性分析，因此研究对象为负荷节点的单端口戴维南等值参数。在此基础上，本文将用于分析电压稳定性的单端口戴维南等值参数在线跟踪方法应用于双端电源等值电势的快速估计，进而实现在线定值。从式（5）与式（10）可知，图4中的送受端系统等值阻抗Z′ss、Z′rr和Z′sr决定于发电机的内电抗和送受端系统网络结构与参数。另外从式（7）、式（8）与式（11）可见，双端电源等值电势˙Eq1和˙Eq2不但决定于电源内电抗与网络结构参数，而且还与各节点的注入有关，现假设无论系统状态如何变化，都认为系统网络结构和参数不变化，而归结为相应节点的注入发生变化，从而当运行条件变化时图4中的等值参数Z′ss、Z′rr和Z′sr将保持不变，而归结于˙Eq1和˙Eq2的变化。

若令˙Us和˙Us已知，则由图4的节点电压方程化简可得

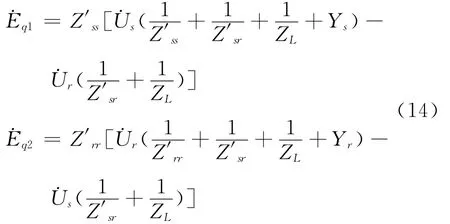
由此可见，只需利用研究线路边界母线所在变电所可测得的线路首末端节点电压相量˙Us、˙Ur，即可在线计算对应当前时刻的等值电势˙Eq1和˙Eq2，从而得到对应当前时刻的等值网络。随着实验数据的不断变化，将得到不同的等值参数˙Eq1和˙Eq2。

2.2 载流量在线定值分析

若令˙Eq1和˙Eq2已知，在图3中由式（1）和式（10）、式（11）可得

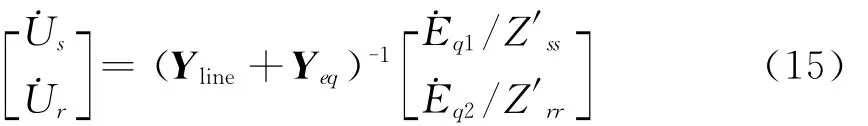
假设δsr为˙Us，˙Ur之间的相角差，由图1可推导得出输电线路送端的注入有功、无功率为

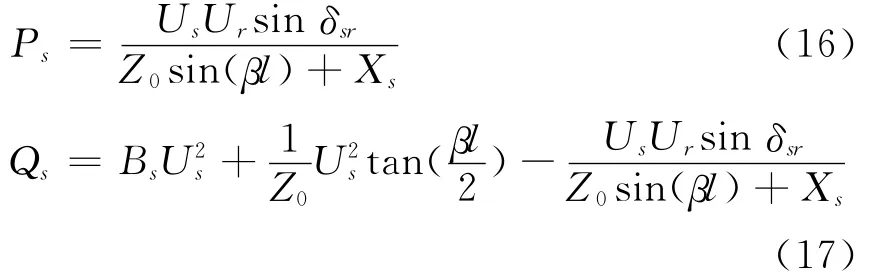
计及忽略电阻的假设，可令

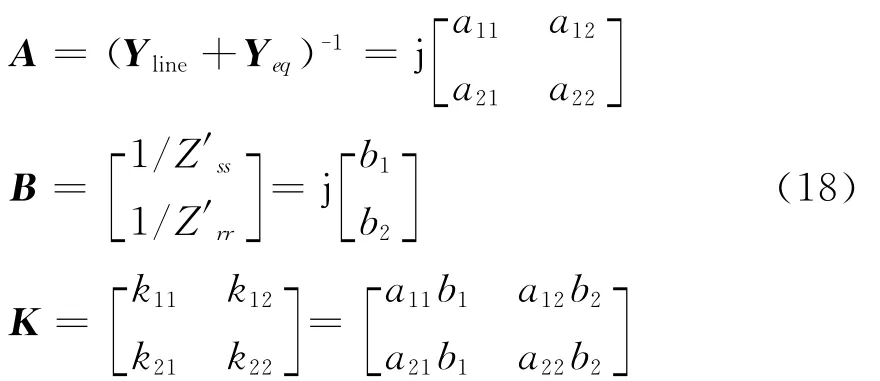
式中，a11、a12、a21、a22、b1、b2、k11、k12、k21、k22均为实数。

假设δ12为˙Eq1和˙Eq2之间的相角差，通过类似式（5）的推导，可得输电线路传输的有功功率为

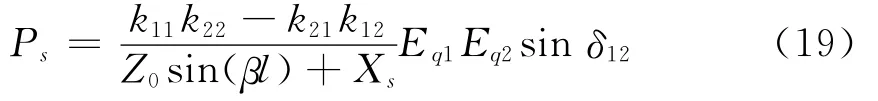
可见，本模型中，Ps与δ12之间仍满足正弦函数关系，当δ12＝90°时，输送功率Ps达到最大值，同时也达到静态稳定极限。

在图4中，随着从送端系统到受端系统传送功率的增加，δ12将增大，在以往文献对输电线路载流定值过程中，系统等值参数不变，这就忽略了系统的非线性和时变性，在实际系统运行过程中，随着线路载荷能力的增加，系统各节点的注入以及各节点的电压、相角乃至系统结构都有可能是变化的，也就是随着δ12的增加，系统等值电势˙Eq1、˙Eq2及等值阻抗Z′ss、Z′rr和Z′sr都将发生变化，从而式（19）中k11、k12、k21、k22、Eq1、Eq2都将是变化的。但基于本文的假设，即无论系统状态如何变化，都认为系统网络结构和参数不变化，而归结为相应节点的注入发生变化，从而式（19）中k11、k12、k21、k22为常数，而Eq1、Eq2都将是变化的，为此要推测出随δ12不断加大时的Eq1、Eq2的值。根据过去几个连续运行状态点，通过式（14）在线计算出Eq1（1）、Eq1（2）、…、Eq1（t），Eq2（1）、Eq2（2）、…、Eq2（t） 和 δ12（1）、δ12（2）、…、δ12（t）。在参数的推测过程中本文采用时间序列法，例如：将Eq1与δ12看成是两组离散的时间序列，求得其对应关系。由此便可求得对应δ12（t＋1），…，δ12（t＋m）的等值参数Eq1（t＋1），…，Eq1（k＋m）。同理可求取随δ12变化的Eq2。由此可以在线推算出运行条件下线路的载荷能力，其具体的求解过程如图5所示。

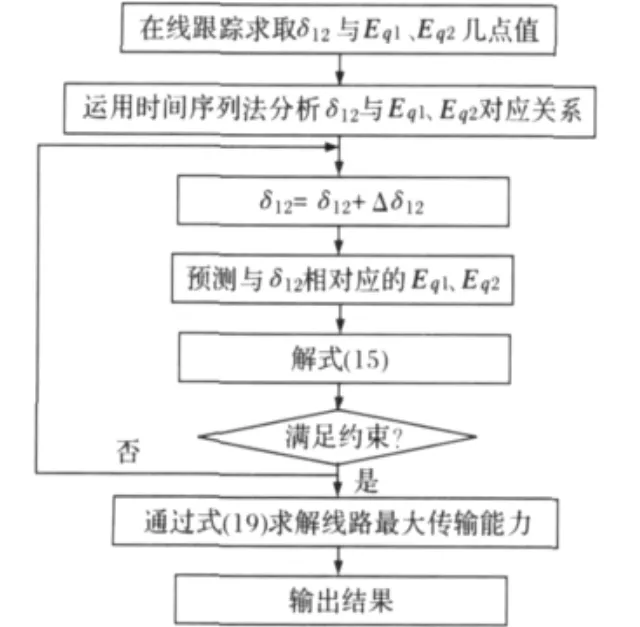
图5 求解过程Fig.5 Solution process

综上所述，根据研究线路边界母线所在变电所可测得的线路首末端节点电压相量˙Us、˙Ur，通过式（14）即可在线计算对应当前时刻的系统等值参数δ12及Eq1、Eq2，通过当前时刻和过去几个采样点的δ12及Eq1、Eq2的值，采用时间序列法推测出δ12及Eq1、Eq2的对应关系。在载流量在线定值计算中，在当前时刻对应值的基础上，增加δ12的值，并根据求得的对应关系预测出随δ12增加的相应的Eq1与Eq2的值。进而在δ12及Eq1、Eq2已知的情况下，通过求解式（15）与式（19）求取最大载流量并分析最大载流量的限制因素。

2.3 时间序列ARMAX法

时间序列预测是根据历史数据建立描述时间序列变化过程的规律性的数学模型，然后根据建立的数学表达式进行预测，其基本假定是“未来是过去的延续”。时间序列分析法适用于平稳时间序列，对于有明显上升和下降趋势的非平稳时间序列可以采用差分法将其转化为平稳时间序列。

时间序列ARMAX预测模型（带外部变量的自回归滑动平均模型）为

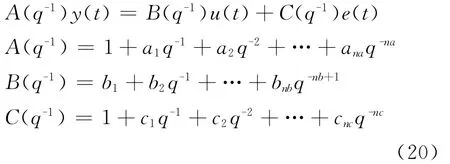
式中：残差e（t）为零均值白噪声序列；a1…ana、b1…bnb、c1…cnc为待估计参数；na、nb、nc 为滞后阶数。na、nc的取值可通过自相关函数（ACF）和偏自相关函数（PACF）的分析确定，nb的取值通过回归系数的显著性分析加以确定。q－1为延时算子，即q－1y（t）＝y（t－1），q－1e（t）＝e（t－1）。

时间序列建模分析预测的基本步骤如图6所示。

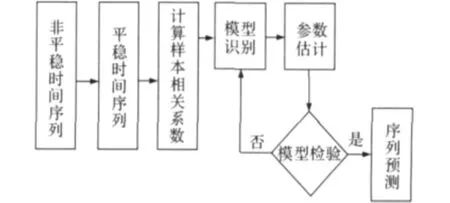
图6 时间序列预测步骤Fig.6 Time series prediction step

2.4 约束条件

进行输电线路载荷能力定值计算需要考虑的主要因素有：热极限、电压水平限制和静态稳定约束。正常运行条件下，电网的电压水平变化不大，因此本文采用额定电压水平下输电线路达到热载流极限时的视在功率作为计算输电线路载荷能力定值的热极限。电压限制可以根据线路的具体情况来设定，本文取送、受端母线电压变化范围为－5%～10%为电压限制约束。我国《电力系统安全稳定导则》中规定静态稳定储备系数Kp应大于15%～20%。考虑到超高压输电线路对整个电力系统稳定运行的重要性，Kp取较高的值是合理的。本文取Kp＝30%，对应的机端相角差为44°，此稳定裕度比安全稳定导则规定的极限水平高，但低于国外计算时设定的稳定性水平。

3 算例及其分析

3.1 算例1

本文采用IEEE39节点电力系统作为算例对本文阐述的模型和算法进行了分析。其网络结构如图7所示，现求取支路6－5的最大载流量及其限制因素。线路运行场景为系统各节点负荷保持定功率因数同步增长，增长的负荷在各发电机之间平均分配。表1给出了对应过去6种不同运行状态的等值参数及线路首、末端节点电压，其中状态0为当前运行状态。假设线路6－5的最大热载荷量为当前0状态支路潮流的2倍，通过本文方法求取的最大载流量为793.81MW，受线路首端电压降约束。

通过连续潮流［12］算得线路载流量为848.01 MW，也是受线路首端节点电压降约束，但利用以往的文献的研究方法，均假设系统等值参数保持当前0状态的等值参数不变，由此求得研究线路最大载流量为热载荷1033.56MW，受导线发热限制，结果如表2所示。表2所列结果表明，不考虑系统等值参数的变化，采用传统算法求得的输电线路最大载流量与通过连续潮流计算的线路实际载流量相差较大，而考虑参数变化后求得输电线路最大载流量与通过连续潮流计算的实际载流量比较接近，误差为6.39%。表2中同时给出了最大载流量所对应时刻的系统等值参数及线路首、末端节点电压。此算例表明了本文提出的输电线路变参数等值模型以参数的变化准确，有效地反映了被等值网络的实时运行状态，通过该模型求得的输电线路载流量更贴切于实际运行条件下的最大载流量。

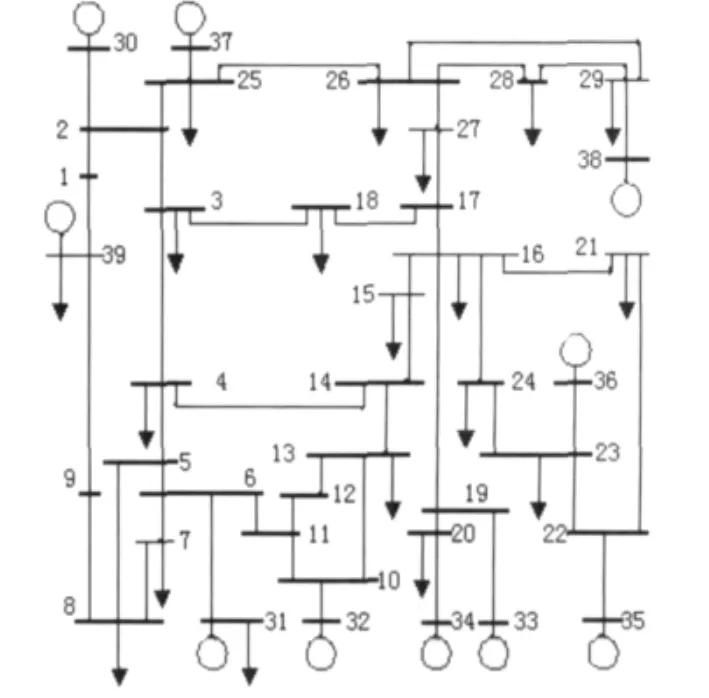
图7 网络结构Fig.7 Network structure

表1 系统等值参数Tab.1 Equivalent parameters of system

表2 载荷能力最大时刻对应等值模型参数Tab.2 Maximum loadability and the corresponding equivalent parameters

3.2 算例2

基于上述，本文对威海电网一条220kV输电线路进行了载荷能力在线定值计算与分析。该输电线路长26.062km，输电线路型号为LGJ－400，热电流极限为845A。

对该输电线路，选取典型日的系统运行参数进行计算，计算表明该输电线路的载荷能力受首末端电压幅值限制，典型日24个小时的输电线路载荷能力在线定值计算结果如图8所示。

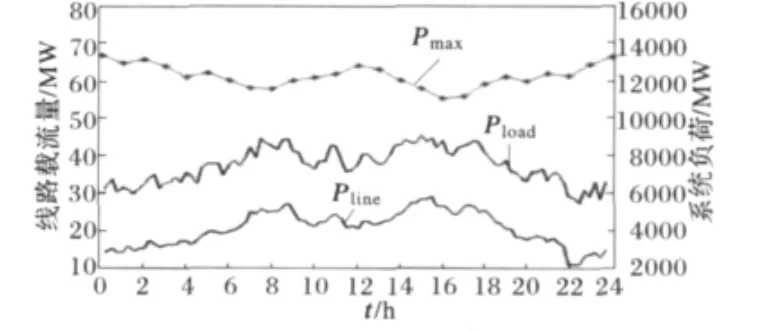
图8 典型日线路载荷及在线定值计算结果Fig.8 Typical day load and the on－line valuation results of transmission line loadability

由图8可见，输电线路的载荷能力随系统的运行状态不断变化。在典型日的前12个时段，输电线路的载荷能力定值在9点处达到最小值，而全天的最小值点则出现在15点，与系统日负荷曲线Pload的两个峰值相对应。这表明，在系统负荷较轻时，输电线路具有较高载荷能力。输电线路的载荷能力在线定值是当前系统运行状态下，输电线路在安全稳定约束域内可传输有功的极限值，电网调度人员可以此为依据，实时跟踪计算输电线路的负载率变化，对输电线路的安全运行状态和变化趋势进行评估。

4 结语

本文在电网实时运行环境下，提出输电线路载荷能力在线定值的概念，这对当今电网紧张状况无疑是有实际价值的。在目前电网技术条件下，在线跟踪系统等值参数已无障碍，完全可行。通过对送受端交流输电系统进行两端口诺顿等值并计及等值电势的变化，考虑了系统的非线性和时变性，并计及了并行流对线路载荷能力的影响，使计算结果更加符合电网运行实际。

［1］常康，韩学山，王孟夏（Chang Kang，Han Xueshan，Wang Mengxia）.电网关键元件及其单调性研究Ⅰ：概念与基础（Study on the crucial element and its monotone in power grid partⅠ：concepts and foundation）［J］.电力系统保护与控制（Power System Protection and Control），2009，37（6）：1－5.

［2］St Clair H P.Practical concepts in capability and performance of transmission lines［J］.AIEE Transactions on Power Apparatus and Systems，1953，72（6）：1152－1157.

［3］Dunlop R D，Gutmn R，Marchenko P P.Analysis development of loadability characteristics for EHV and UHV transmission lines［J］.IEEE Trans on Power Apparatus and Systems，1979，98（2）：606－617.

［4］Gutman R.Application of line loadability concepts to operating studies［J］.IEEE Trans on Power Systems，1988，3（4）：1426－1433.

［5］柴旭峥，梁曦东，曾嵘（Chai Xuzheng，Liang Xidong，Zeng Rong）.交流输电线路输送能力曲线计算方法的改进（An improved calculation method for power－transmitting capability curve of AC transmission line）［J］.电网技术（Power System Technology），2005，29（24）：20－24.

［6］徐政（Xu Zheng）.超、特高压交流输电系统的输送能力分析（EHV／UHV ac transmission capability analysis）［J］.电网技术（Power System Technology），1995，19（8）：7－12.

［7］刘天琪，李兴源（Liu Tianqi，Li Xingyuan）.交直流联络线局部控制的变参数等值模型（Variable parameter equivalent model for ac／dc parallel tie－line local control）［J］.电力系统自动化（Automation of Electric Power Systems），2001，25（8）：7－11.

［8］王漪，柳焯（Wang Qi，Liu Zhuo）.基于戴维南等值的系统参数跟踪估计（Tracking and estimation of system parameter using Thevenin＇s equivalent）［J］.电 网 技 术（Power System Technology），2000，24（11）：28－30.

［9］王芝茗，王漪，徐敬有（Wang Zhiming，Wang Qi，Xu Jingyou）.关键负荷节点集合电网侧戴维南参数预估（Prediction of Thevenin＇s equivalent parameters on electrical power network side for the muster of key load nodes）［J］.中国电机工程学报（Proceedings of the CSEE），2002，22（2）：16－20.

［10］葛少云，李晓明（Ge Shaoyun，Li Xiaoming）.基于戴维南等值的配电网合环冲击电流计算（Study on surge current due to closing loop in distribution network based on Thevenin＇s equivalent）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2007，19（6）：124－127.

［11］DL755－2001，电力系统安全稳定导则［S］.

［12］蔡伟程，代静（Cai Weicheng，Dai Jing）.对求取电力系统PV曲线的连续潮流法的改进（Improvement of continuation method in tracing PV curves of power systems）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2005，17（5）：82－85.