SVM－DTC控制的永磁同步伺服系统仿真

黄彦婕，周扬忠，江修波，蔡金锭

（福州大学电气工程与自动化学院，福州 350108）

永磁同步电动机（PMSM）体积小、重量轻、效率高，转子没有发热问题，控制系统较一般电动机简单［1］，从而在伺服驱动领域得到广泛应用［2］。伺服系统要求稳态误差尽可能小，同时要求有尽可能高的动态响应速度，以及位置响应无超调。目前PMSM伺服系统的控制策略主要为矢量控制（VC），VC稳态性能好，但转矩动态性能逊色，控制性能受转子参数变化的影响较大。为此，学者们提出了直接转矩控制策略（DTC）。DTC的转矩动态响应快，但传统DTC的转矩脉动大［3，4］，低速稳态性能较差，所以限制了其在PMSM伺服系统中的应用。因此，本文在永磁伺服系统中引入基于空间矢量调制的直接转矩控制策略（SVM－DTC），旨在保持伺服系统优越的低速稳态性能的同时，大幅度地提高系统动态响应速度，及伺服系统对参数变化的鲁棒性。

1 永磁同步电机数学模型

对称绕组PMSM在转子同步旋转d－q坐标系下的数学模型［5］如下所示。

定子电压方程为

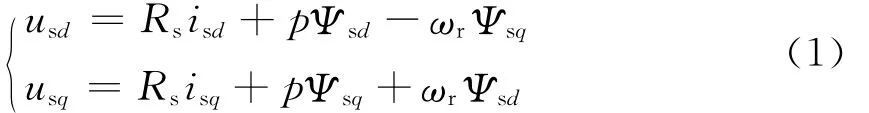
定子磁链方程为

电磁转矩方程为

转子机械运动方程为

式中：p为微分算子；usd、usq、isd、isq、Ψsd、Ψsq、Ld、Lq分别为d、q轴上的定子电压、电流、磁链、电感分量；Rs为定子相绕组电阻；ωr为转子速度；Ψfs为转子永磁体在定子上产生的耦合磁链；TL为负载转矩；pn为磁极对数；J为转动惯量。

定子磁链定向坐标系中电磁转矩可表示为

式中：｜Ψs｜为定子磁链幅值；δ为转矩角，控制δ即可控制Te。

2 SVM－DTC伺服控制系统原理及方案

PMSM位置伺服控制系统由外到内依次为位置、速度、转矩闭环。位置闭环将根据上位机给定的位置和编码器检测的转子位置偏差，经PI调节器得到转子的给定速度。速度闭环同样通过PI调节器，计算出应达到的电磁转矩给定。最后利用基于直接转矩控制策略的转矩内环实现转矩的快速控制，从而实现转子位置角的快速而平稳的控制。控制策略结构如图1所示。

图1 SVM－DTC伺服系统控制结构Fig.1 Scheme of servo control system with SVM－DTC

直接转矩控制的基本思想为保持定子磁链幅值不变，通过控制定、转子磁链的夹角来控制电磁转矩。将速度闭环得到的电磁转矩及观测得到的电磁转矩Te通过PI调节器得到定子磁链矢量在下一个控制周期内期望的旋转角度Δδ＊smk＋1（转矩角增量）。再根据式（6）和式（7），求得定子磁链的增量［6］为

定子磁链旋转速度及幅值直接取决于外施电压矢量，既利用电压矢量可以实现对转矩角的快速控制。PMSM电压方程离散化可得到参考电压矢量计算式为

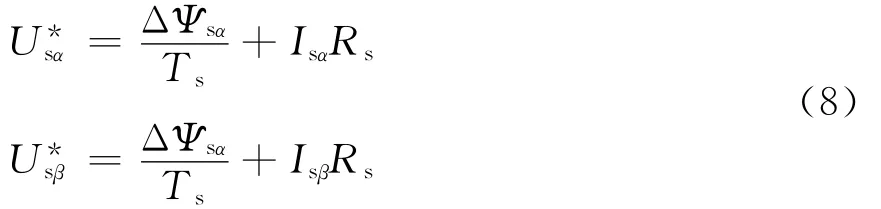
最后通过空间矢量调制SVPWM（space vector pulse width modulation）在一个控制周期中选择相邻非零电压矢量和零矢量，并计算每个矢量的作用时间，从而合成所需的电压矢量，实现转矩和磁链的无差控制。

3 SVM－DTC伺服控制系统建模及仿真

在MATLAB simulink环境中搭建SVM－DTC伺服系统，系统模型如图2所示。主要包括：根据数学模型建立的PMSM模块，磁链观测模块，DTC控制模块和SVPWM模块。其中DTC模块根据式（6）～ 式（8），通过MATLAB Function模块编写参考电压的计算程序予以实现。SVPWM模块采用矢量在控制周期分7段发出的方式，使定子磁链旋转更加平稳，产生的转矩脉动相应减小。对所建立的PMSM伺服控制系统进行仿真，采用电机参数如下：定子相绕组电阻Rs＝1Ω，交直轴电感Ld＝Lq＝0.007H，转子永磁体在定子上产生的耦合磁链Ψfs＝0.42Wb，转动惯量J＝0.04 kg·m2，磁极对数pn＝2。设直流母线电压Udc＝500V，给定定子磁链幅值恒等于转子永磁体在定子上产生的耦合磁链。

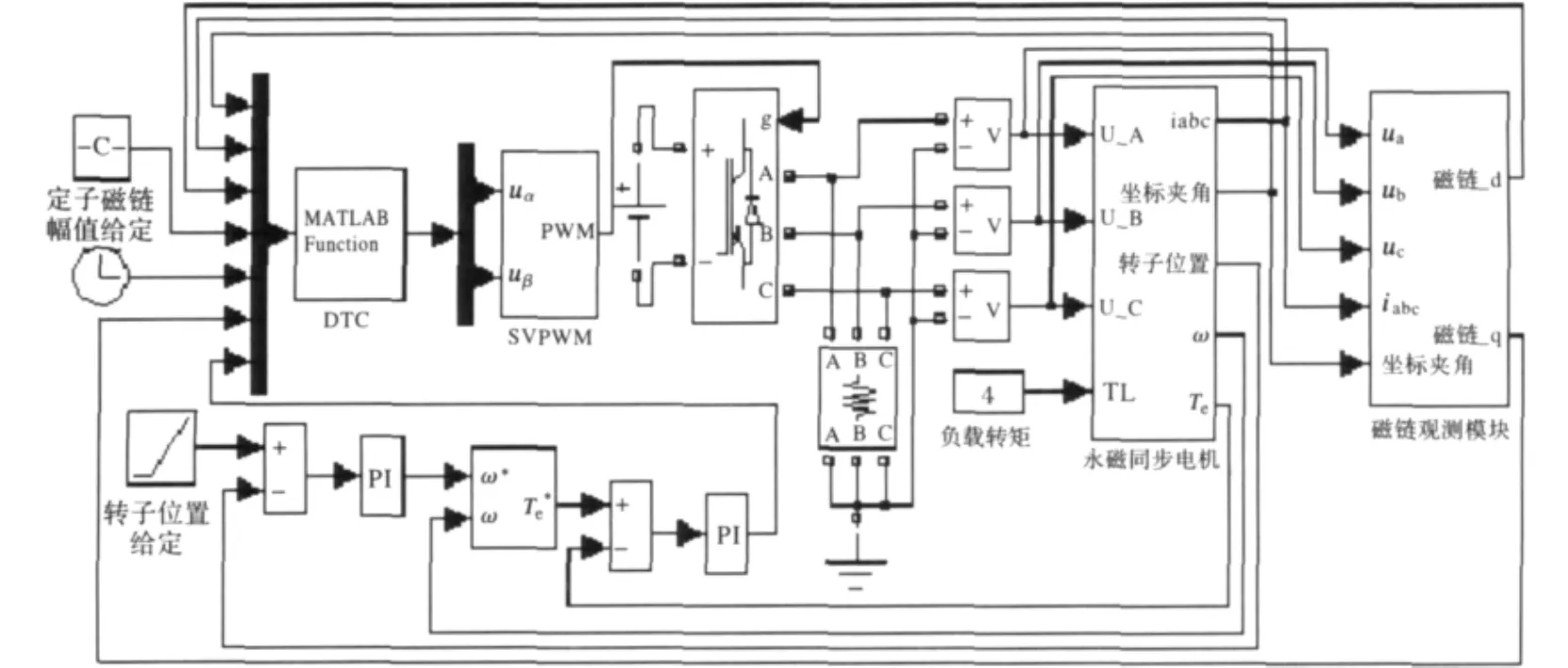
图2 SVM－DTC伺服控制系统仿真模型Fig.2 Simulation model of servo control system with SVM－DTC

3.1 转矩动态响应及其稳态性能仿真

负载转矩恒为3N·m，控制周期80μs，给定方波转矩幅值为±63N·m。SVM－DTC伺服系统的转矩动态及其稳态仿真结果如图3和图4所示，

图3 转矩动态响应仿真波形Fig.3 Simulation waveforms of torque dynamic response

为了对比方便，图3和图4还给出了同等条件时的VC伺服系统仿真波形。图3可见SVM－DTC转矩响应快，响应时间仅为2.5ms，VC则需4ms。同时由图4可见，电机在给定转矩为9.5N·m时，SVM－DTC的转矩脉动最大为±0.125N·m，而VC转矩脉动最大则达 ±0.85N·m。可见SVM－DTC系统具有转矩动态响应迅速，稳态转矩脉动小的优点。

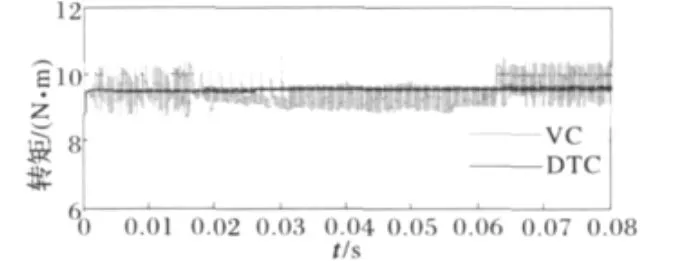
图4 稳态转矩脉动仿真波形Fig.4 Simulation waveforms of steady－state torque

3.2 鲁棒性分析

转速给定为1 500r／min，负载转矩在0.2s时从3N·m突变到15N·m。图5为SVM－DTC和VC两种控制方式下伺服系统的速度响应波形，从图中可见SVM－DTC伺服系统在0.2s突加负载时最大速降为1r／min，而VC伺服系统最大速降为19r／min。

图6为给定位置5rad时，两种控制方案的位置跟踪状态。在0.5s时使负载转矩从3N·m突变到15N·m。图6中SVM－DTC伺服系统在0.5s突加负载时最大位置误差为0.01rad，而VC伺服系统最大位置误差为0.11rad。

图5 负载扰动对速度伺服影响仿真波形Fig.5 Speed waveforms of servo system under load disturbances

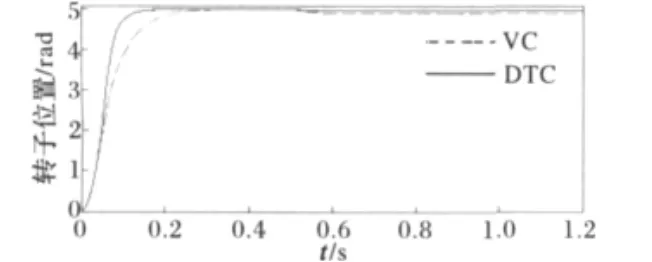
图6 负载扰动对位置伺服影响仿真波形Fig.6 Position waveforms of servo system under load disturbances

从上述仿真结果可见SVM－DTC伺服系统具有抗负载扰动干扰的强鲁棒性。

3.3 动态位置跟踪仿真

给定一斜坡位置信号，同时在0.15s使负载转矩由3N·m突变到15N·m。位置、转速、转矩、定子磁链轨迹波形如图7所示。

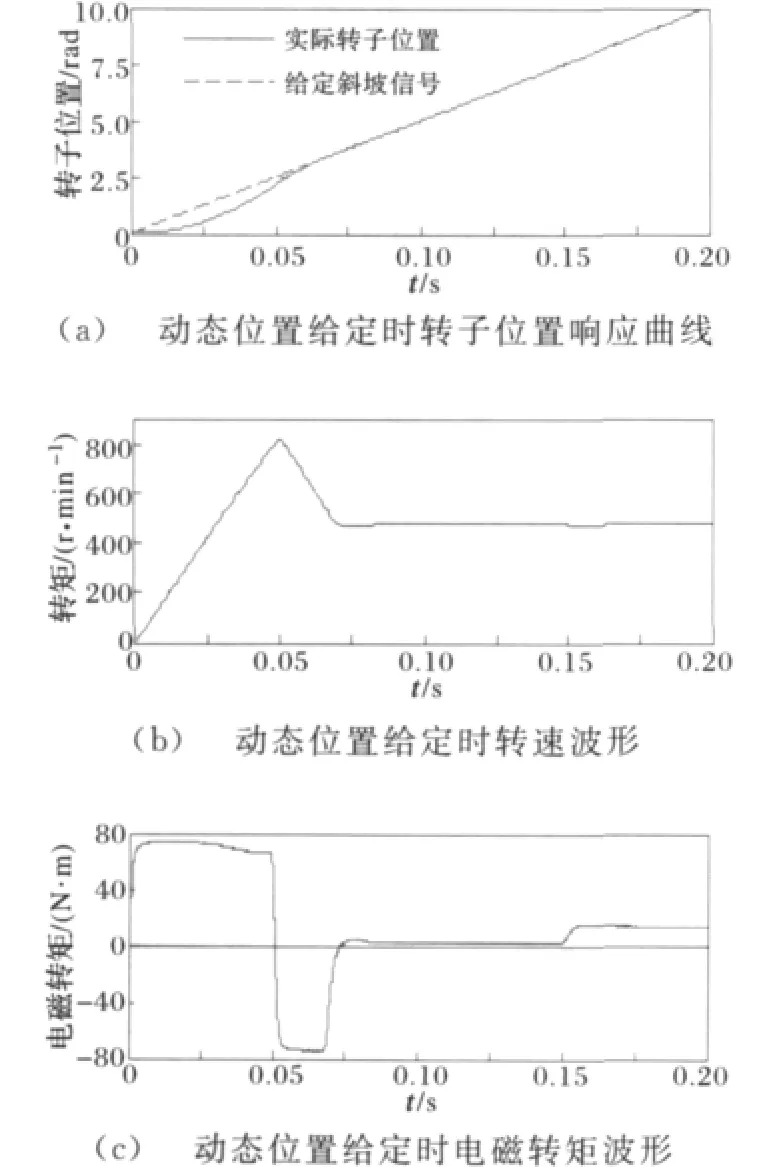
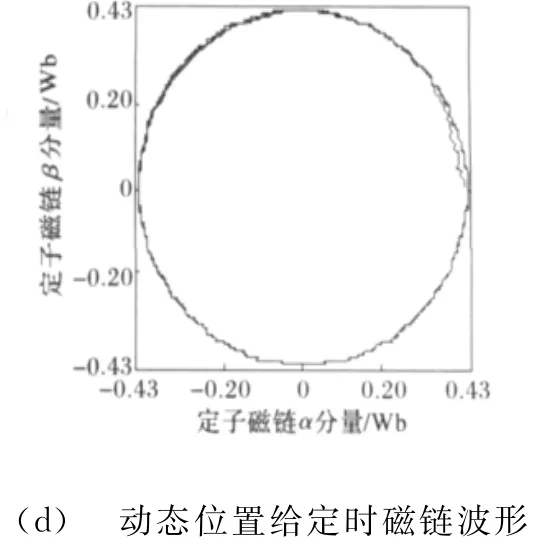
图7 动态位置给定时位置、速度、转矩、磁链波形Fig.7 Position，speed，torque and magnetic chain waveforms under given dynamic position

图7中，转子在0.066s达到给定的位置，无超调，此后一直准确跟踪。电磁转矩在加速过程中保持最大电磁转矩±75.6N·m，转速稳定后转矩脉动小于0.2N·m，且起始时刻转矩响应时间仅3 ms。同时，从图7的定子磁链圆可看出磁链幅值始终保持在0.42Wb，脉动很小。0.15s负载转矩突变时，电磁转矩响应时间仅4ms，稳定过程中转速最大脉动6r／min，经10ms再次跟踪至给定位置，抗干扰性能优越。

通过上述的仿真可看出将SVM－DTC用于伺服系统，提高了系统的响应速度及抗外部干扰的鲁棒性，同时具有高稳态精度。

4 结语

基于永磁同步电动机的速度（位置）伺服系统是目前的一个研究热点，需要解决的问题主要包括系统响应的快速性和对参数变化及外部扰动的鲁棒性。

本文利用直接转矩控制思想结合SVPWM技术，建立了PMSM伺服控制系统的仿真模型。研究结果表明：

①SVM－DTC伺服系统转矩动态响应迅速；

②SVM－DTC伺服系统稳态控制精度高；

③SVM－DTC伺服系统对负载扰动抑制能力强，对电机参数变化具有很强的鲁棒性。

以上研究结果为SVM－DTC用于实际伺服系统的设计与调试提供了思路和基础。

［1］钟技（Zhong Ji）.永磁同步电动机新型直接转矩控制研究（Research on the Novel Direct Torque Control for the Permanent Magnet Synchronous Motor）［D］.福州：福州大学电气工程及其自动化学院（Fuzhou：College of Electrical Engineering and Automation，Fuzhou University），2010.

［2］陈吉红（Chen Jihong）.发展我国伺服驱动产业的探讨（Discussion of development of Chinese servo drive industry）［J］.航空制造技术（Aeronautical Manufacturing Technology），2006，（8）：46－49.

［3］苏陈云，杨向宇（Shu Chenyun，Yang Xiangyu）.永磁同步电机直接转矩控制转矩脉动的产生及其抑制方法综述（Torque ripple reduction and generation of permanent magnet synchronous based on direct torque control）［J］.微电机（Micromotors），2010，43（3）：81－85.

［4］王斌，王跃，王兆安（Wang Bin，Wang Yue，Wang Zhao＇an）.空间矢量调制的永磁同步电机直接转矩控制（Direct torque control of permanent magnet syn－chronous motor drives using space vector modulation）［J］.电机与控制学报（Electric Machines and Control），2010，14（6）：45－50.

［5］何继爱，王惠琴（He Ji＇ai，Wang Huiqin）.永磁同步电机空间矢量控制系统的仿真（Simulation of PMSM controlled by space vector PWM）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2005，17（6）：14－16，38.

［6］周扬忠.交流电动机直接转矩控制［M］.北京：机械工业出版社，2009.