曲边梯形面积常用近似计算方法在Excel 中的实现
欧阳和平 刘姣娥 阳 晖
(湖南食品药品职业学院 湖南 长沙 410014)
0 引言
在科学研究、工程和生产实践中,往往要碰到求曲边梯形面积的问题。 在直角坐标系中,曲边梯形面积是指由曲线y=f(x)和直线x=a、x=b 及y=0 所围成的面积。这里,f(x)>0,b>a。该曲边梯形面积,在数学上可以通过计算被积函数为f(x),积分下、上限分别为a 与b 的定积分来得到。 当被积函数f(x)能用初等函数表达,在积分区间连续,并且能找到f(x)的原函数F(x),那么,定积分的值S=F(b)-F(a)。但当f(x)不能用初等函数来表达,或只是一些实验得出来的经验值序列,或f(x)的原函数F(x)不能用初等函数来表达,则S 只能通过近似计算来求得。 求曲边梯形面积近似值的方法有矩形法、 梯形法和抛物线法等多种,具体可采用图解法、计算机编程来计算,但都有一定的局限性。图解法受绘图界面所限制,不可能将曲边梯形分得太小,计算繁琐且不精确。计算机编程又不是一般人都能掌握的,就是掌握了也不是在所有场合都适应的。 本文提出一种用Microsoft Excel 计算曲边梯形面积近似值的简单而又实用的方法。
1 Excel 计算曲边梯形面积的方法
前已述,求曲边梯形面积近似值的方法有矩形法、梯形法和抛物线法。 不管是哪种方法都是先将曲边梯形细分成若干小曲边梯形,接着分别计算出各小曲边梯形面积的近似值,最后将各小曲边梯形的近似值之和作为整个曲边梯形面积的近似值。 所不同的是:矩形法将每个小曲边梯形的曲边用一条水平直线来代替,因而小曲边梯形就变成了小矩形,计算小曲边梯形面积就变成了计算小矩形面积;而梯形法则是将每个小曲边梯形的曲边以一条连接两个交点的直线段来代替,这样小曲边梯形就变成了小梯形,计算小曲边梯形面积就变成了计算小梯形面积;抛物线法则是以抛物线上的一段弧代替小曲边梯形的曲线弧,从而计算出定积分的近似值。
用分点将区间[a,b]分成n 个小区间,对应区间长分别为Δx0,Δx1,…,Δxn-1,Δxn,并设函数f(x)对应于各分点的函数值分别为f(x0),f(x1),…,f(xn-1),f(xn),那么,
矩形法表示的曲边梯形的面积为:

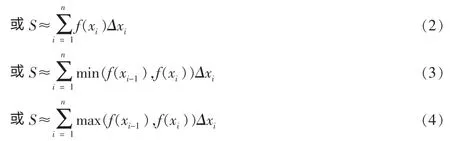
上述四个公式代表四种方法。 四种方法虽然都是矩形法,但其意义有所不同。 矩形法1 以左边高f(xi-1)作为小矩形的高,矩形法2 以右边高f(xi)作为小矩形的高,矩形法3 以f(xi-1)、f(xi)中较小作为小矩形的高,矩形法4 以f(xi-1)、f(xi)中较大作为小矩形的高。
梯形法表示的曲边梯形的面积为:

值得注意的是, 矩形法和梯形法的小区间划分并不一定要均分,这要根据f(x)在积分区间的特征来决定。
抛物线法又称辛普森(Simpson)法。 抛物线法表示的曲边梯形面积相对复杂一些。为简单起见,将区间[a,b]分成n 个均等的小区间,且n 为偶数,由于各区间长度相等,抛物线法表示的曲边梯形面积公式为:
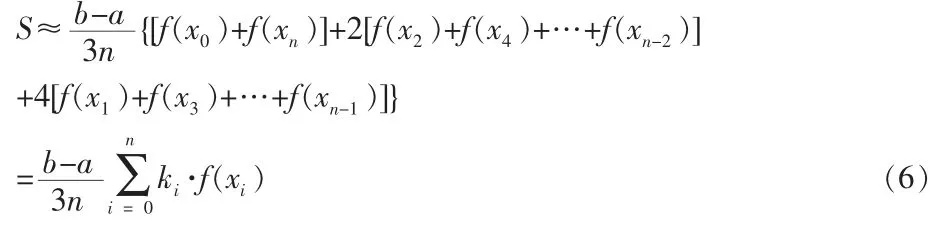
式中,n 为偶数;ki序列为1,4,2,…,2,4,1。
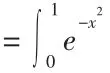
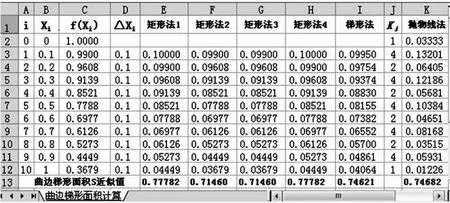
图1
首先在A 列输入分点的序号,B列用等差数列自动填充方法填入各分点的xi值。 C 列根据xi值计算出对应的f(xi)值。 方法是先在C2单元格输入公式“=EXP(-(B2^2))”,计算出f(x0),然后用填充柄向下填充,求出所有其他的f(xi)值。 在D 列的D3 单元格输入公式“=B3-B2”,计算出Δx1,用填充柄向下填充得到其他的Δxi值。 由于是均分各点,所以所有的Δxi都相等。
接着根据矩形法曲边梯形面积近似计算公式(1)~(4)计算出用来近似10 个细分的小曲边梯形面积的小矩形面积。 每种方法的第一个小矩形面积的计算公式分别为 “=C2*D3”、“=C3*D3”、“=MIN(C2:C3)*D3”和“=MAX(C2:C3)*D3”,依次应用于单元格E3、F3、G3 和H3 即计算出它们的值,然后用填充柄向下填充求出其他小矩形面积。 在最后一行,用求和函数“=SUM(E3:E12)”、“=SUM(F3:F12)”、“=SUM(G3:G12)”和“=SUM(H3:H12)”依次求出对应列中各小矩形面积之和,即为分别用矩形法1、矩形法2、矩形法3 和矩形法4 计算出来的曲边梯形面积的近似值。
在I 列应用梯形法曲边梯形面积近似计算公式(5)比照矩形法相似的计算方法算出10 个小梯形面积。 方法是在I3 单元格中输入公式“=(C2+C3)/2*D3”求出第一小梯形的面积,然后用填充柄向下填充求出其他小梯形面积。 在最后一行,用求和函数“=SUM(I3:I12)”求出I 列中各小梯形面积之和,即为用梯形法计算出来的曲边梯形面积的近似值。
抛物线法计算在K 列进行,计算依据是公式(6)。 计算前应确定J列的ki,根据公式(6),k0=1,kn=1,其它的以4 和2 交替出现,可以用填充柄以4、2 向下填充实现。 然后选择K2,输入公式“=J2*C2*(1-0)/3/A$12”,计算出k0·f(x0)*(b-a)/3/n,然后用填充柄向下填充至K12,求得其它各值。 再在最后一行,用公式“=SUM(K2:K12)”求出K 列中各数据之和,即为用抛物线法计算出来的曲边梯形面积近似值。
2 Excel 计算曲边梯形面积的误差估计
这里先介绍梯形法和抛物线法的误差估计方法,只考虑区间[a,b]均分的情况。
公式中涉及到f(x)的一到四阶导数。 对于梯形法,必须f″(x)存在,并且能估计出界值M,误差Rt才能正确求出。 对于抛物线法,必须f(4)(x)存在,并且能估计出界值M,误差Rs才能正确求出。
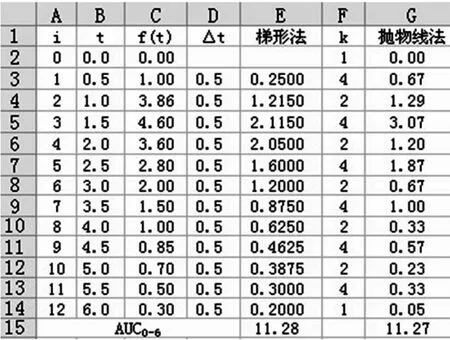
对于上述的例子,可求得梯形法M 为2,抛物线法M 为12。 当取n=10,Rt≤(1-0)3·2/12/100=0.00167, 于是有0.744544129 用矩形法、梯形法和抛物线法求曲边梯形面积近似值时,一般来说,n 取得越大,近似程度就越好。 在Excel 环境下,我们使用填充柄的智能作用,可以很方便地用增加n 的方法来求取更精确的结果。 对于上例,当取n=10,用梯形法和抛物线法得出的结果分别是0.74621和0.74682,如图1 所示;当取n=100,Δx 短小到图1 的1/10,求得结果是0.746818 和0.746824;当取n=1000,Δx 短小到图1 的1/100,结果分别是0.74682407149 和0.746824132812436;当n=10000,Δx 短小到图1 的1/1000,结果是0.74682413219 和0.746824132812428。此例n 由1000 增加到10000 时,用抛物线法计算有13 位小数相同,说明精度已达到了10-13;而梯形法只有6 位小数相同,前6 位小数应该是可靠的。 表1 血药浓度数据 矩形法精度相对较差,但矩形法1 和矩形法2 的平均值或矩形法3 和矩形法4 的平均值就是梯形法的值。 当f(x)在每个小区间都是单调增加或单调减少的非负函数时, 矩形法3 产生的误差永远是负偏差,而矩形法4 产生的误差永远是正偏差。 这在那些要求计算不能产生负偏差或正偏差的场合用矩形法3 和矩形法4 将是合理的选择。对于小区间非均分的梯形法求解,误差可分段估计然后再予综合考虑。 曲边梯形面积计算在多个领域都有应用,这里仅举医药领域生物利用度中应用的例子。 【例】一组健康受试者单剂量,空腹口服某药溶液剂1g,服药前采空白血作对照,2 小时后进餐,每隔一定时间采血样,测定血中药物浓度,结果见表1,求该药溶液剂的AUC0-6。 图2 分析:此题求AUC0-6就是求曲边为血药浓度曲线,积分下、上限为0 与6 的曲边梯形面积,可用梯形法或抛物线法中的任意一种方法计算。 这里将两种方法计算的过程及结果同时给出。 方法:确定n=12,在B 列和C 列输入表1 中数据,在D 列和F 列确定Δt 和k, 然后分别按梯形法和抛物线法计算出该曲边梯形面积的近似值即是AUC0-6的近似值。计算结果详见图2 所示。从图中可以看出,用梯形法算得AUC0-6=12.28,用抛物线法算得AUC0-6=12.27,比较接近。 Excel 计算曲边梯形面积近似值概念清晰,方法简单明了,操作容易掌握,误差可控。 Excel 的突出优点是可以把小区间分得很细,大量的计算由填充柄填充得到, 人们轻轻松松就可将很复杂的计算完成,突破了图解法和计算机编程计算的局限性, 是定积近似理论与Excel智能方法的完美结合,可广泛应用于理论分析、科学研究、工程计算和生产实践中。 [1]华罗庚.高等数学引论(第一卷,第一分册)[M].北京:科学出版社,1963:291-336. [2]同济大学数学教研室,主编.高等数学(上册,第四版)[M].北京:高等教育出版社,1996:306-314. [3]康博创作室.Office 2000 中文版易学易用专辑[M].北京:人民邮电出版社,1999:149-169. [4]Excel Home.Excel 应用大全[M].北京:人民邮电出版社,2008. [5]Excel Home.Excel 2010 应用大全[M].北京:人民邮电出版社,2011. [6]欧阳和平,阳晖.VS 环境下假设检验Web 应用程序开发[J].计算机与现代化,2012(10):187-190,193.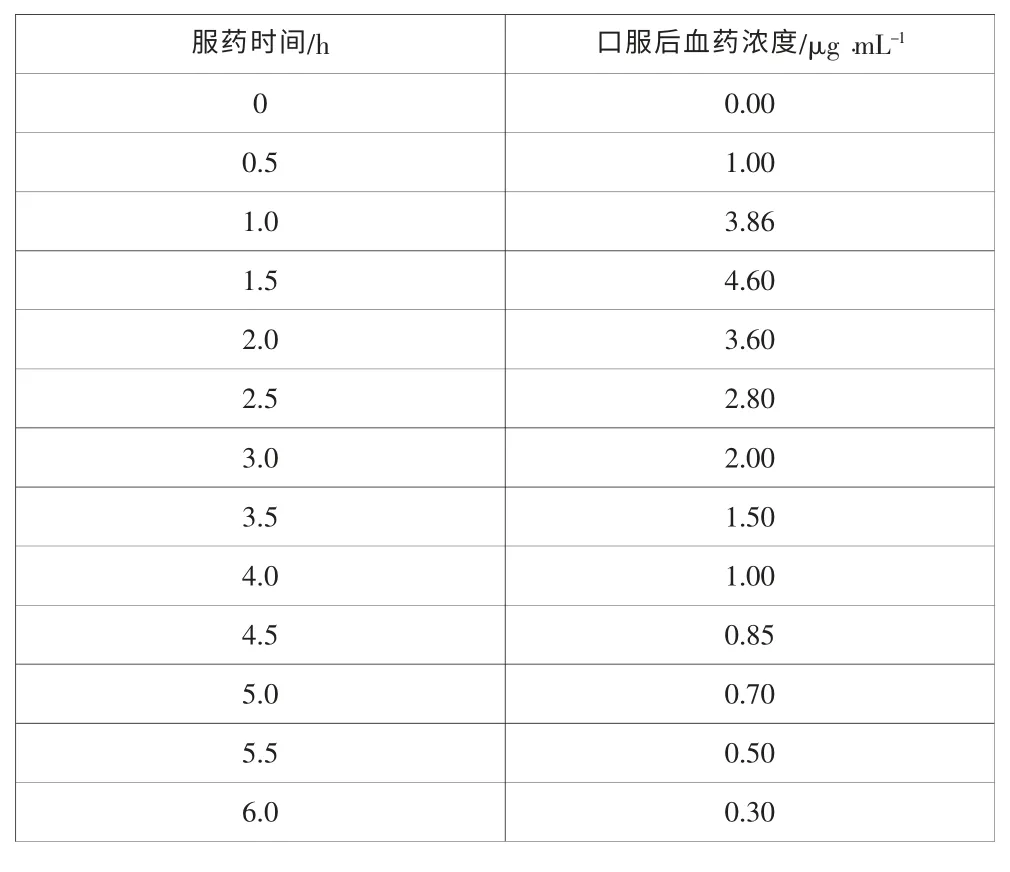
3 Excel 计算曲边梯形面积的应用举例
4 结束语

