利用悬臂梁内力图规律绘制刚架的内力图
王淑琴
(甘肃工业职业技术学院,甘肃天水 741025)
可以说准确快速地绘制出静定刚架的内力图是结构力学学习中的一个基本功,同时也是令师生双方都感到头疼的一个难点。大多数学生就是由于静定刚架的弯矩图没有很好掌握,给后续结构位移计算及力法的学习带来困难。
笔者认为刚架内力图难以掌握的原因有以下方面:刚架一般是由许多横竖直杆组成,杆件数目多。内力的计算如果沿用一般教材介绍的截面法,计算繁琐速度慢,容易出错。第二个原因是材料力学中接触到的梁多数是水平直杆,只要区分上侧受拉还是下侧受拉即可。但是刚架弯曲方向多变、杆件受拉侧不易准确判断,所以令多数初学者感觉眼花缭乱、无从下手,从而导致多数学生对刚架内力图的绘制望而生畏。本文介绍一种利用悬臂直梁的内力图特点应用于刚架内力的计算和内力图的绘制方法。
1 掌握本法需要事先掌握的规律和技巧
1.1 要快速绘制刚架内力图首先需要掌握规律法(简易法)计算直梁内力的方法
直梁内力图规律:梁内任一横截面上的剪力等于该截面一侧与截面平行的所有外力的代数和,绕截面顺转的外力产生正剪力,反之产生负剪力;梁内任一横截面上的弯矩等于该截面一侧所有外力对该截面形心的力矩的代数和。至于刚架弯矩图,土木工程要求画在受拉侧所以弯矩的符号已不重要,关键要判断出杆件哪一侧受拉。
1.2 判断杆件受拉侧的简便方法——悬臂梁法
把所计算的截面固定起来,另一侧的支座去掉,代替以支座反力(计算截面直杆的一侧就变成悬臂梁)。将每种荷载单独作用于该梁,观察梁的变形情况来判断哪一侧受拉,受拉侧即为凸出的一侧。对于不同侧受拉力矩给予相反的符号。多种荷载同时作用时弯矩的数值等于各荷载单独作用于悬臂梁时对该截面产生的力矩之和。表1给出悬臂直梁在常见荷载作用下固定端的内力值及固定一端的截面受拉侧的判断,希望对初学者有帮助。
说明:如果所受荷载与图中反向,则剪力符号与表1中相反。弯矩符号根据实际变形判断出受拉侧。
2 实例应用
1)如图1所示简支刚架,将刚架在刚结点C,D处截开可将该结构分成AC,DB,CD三段。AC,DB就变成图1a),图1b)悬臂梁,把刚连接变成固定端支座。即将静定梁分为几段直梁,绘出直梁的弯矩图汇总于刚架即得刚架弯矩图。
由平衡方程得:
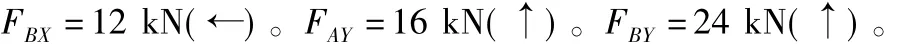
先计算竖杆:AC段,以C截面为界向下部分为直杆C截面的弯矩剪力可用以上规律直接看出QCA=-2×6=-12 kN(因为CA上的均布荷载绕C截面逆时针转所以取负号)。
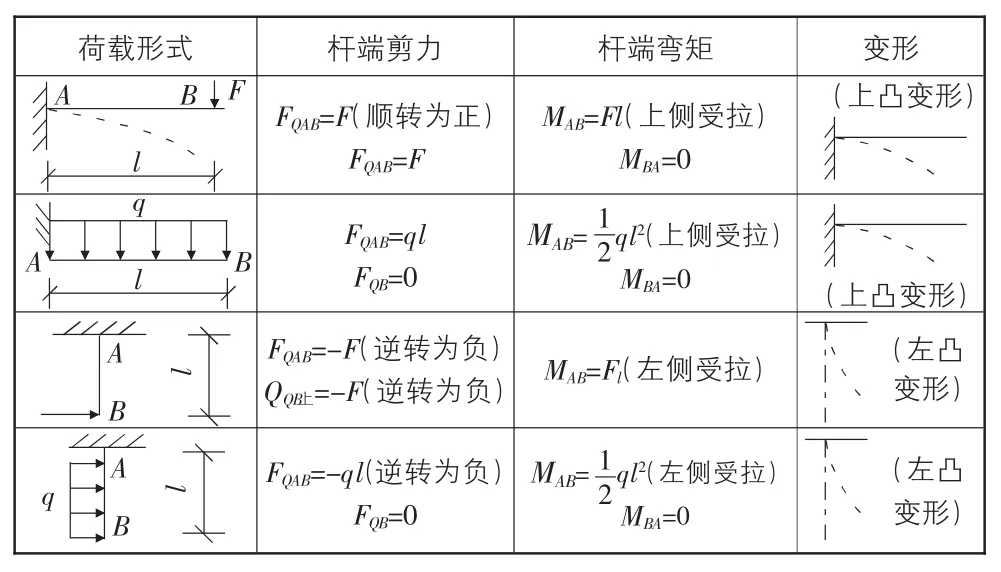
表1 悬臂直梁在常见荷载作用下固定端的内力值及截面受拉侧
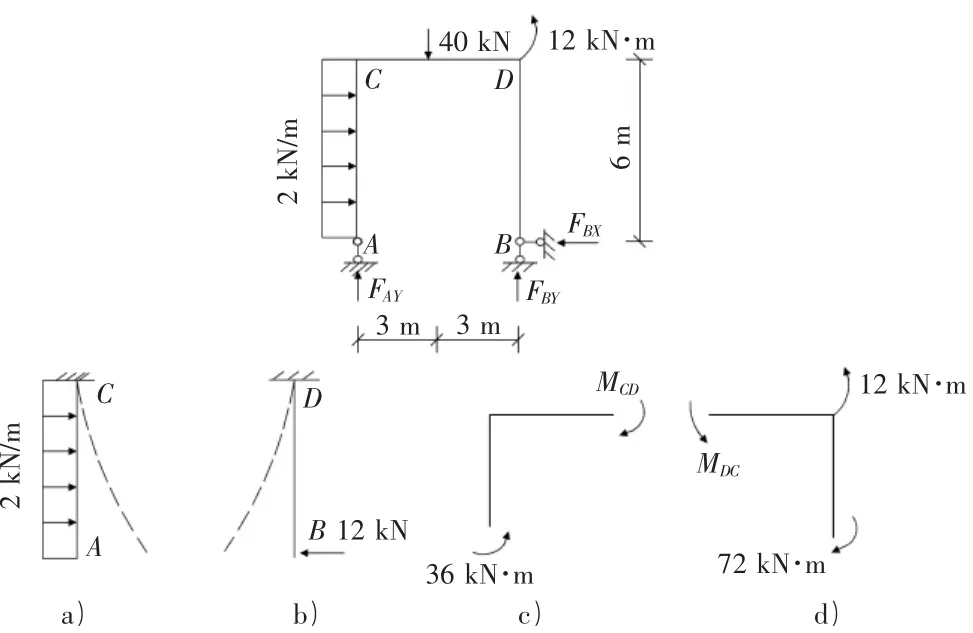
图1 简支刚架
MCA=2×6×3=36 kN·m。C截面弯矩就等于C截面以下部分荷载对该截面产生的力矩之和,固定C截面观察AC段的变形可判断出是左侧受拉。该段的内力图等同于图1a)悬臂梁,因为C处的刚连接与固定端支座的约束性质相同,所以今后对于直杆部分都可将刚结点变成固定端,将所计算部分改造成悬臂梁,只要熟悉了悬臂梁的内力图,刚架的图也就不难了。
按此法,QDB=12 kN,MDB=12×6=72 kN·m(右侧受拉)。
对于横梁CD段的C截面和D截面的弯矩就可利用刚结点平衡原理∑MC=0,如图1c)所示。MCD=MCA=36 kN·m(上侧受拉)。
∑MD=0,如图1d)所示。
MDC=12×6-12=60 kN·m(上侧受拉)。
从CD杆的C截面切开看AC段,与C截面平行的外力为FAY=16 kN,且绕C截面顺转所以可得QCD=16 kN;同理,D截面切开看DB段,与D截面平行外力为FBY=24 kN,且绕D截面逆时针转动。故有QDC=-24 kN。只要所取脱离体为直杆,都可用以上方法计算内力,判断符号。运用由梁荷载集度、剪力、弯矩三者的微分关系确定的内力图规律即可作出内力图(见图2)。CD段的弯矩图要用区段叠加法绘出。
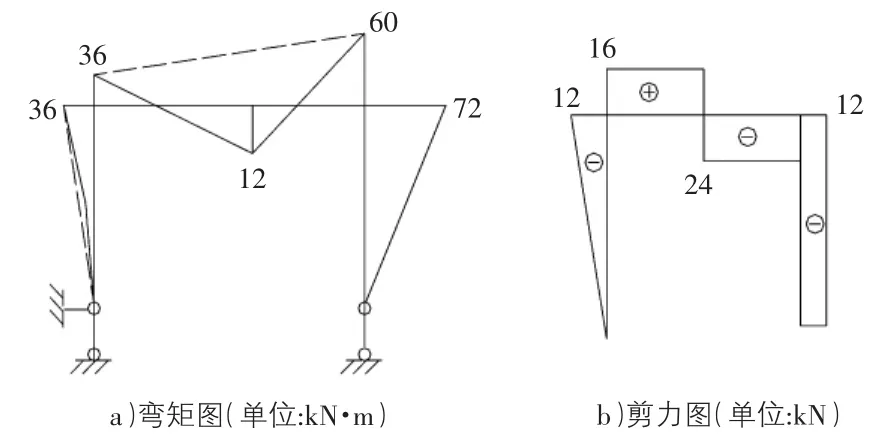
图2 内力图
2)再如以下三铰刚架,也可利用以上方法作出弯矩图(剪力图从略)。先计算支座反力(反力方向如图2所示)。
FAY=60 kN(↓)。
FBY=60 kN(↑)。
FAX=90 kN(←)。
FBX=30 kN(←)。
由于只绘制弯矩图,故只需计算出水平反力即可。
以DE两刚结点为界将刚架分为AD,DE,EB三段。首先计算竖杆DA,EB。两竖杆的内力计算如图3a)所示。AD段弯矩图的绘制可参照图3a),按照荷载分解成图两种情况,弯矩图按照两图叠加。受拉侧的判断可根据图示悬臂梁的变形情况。
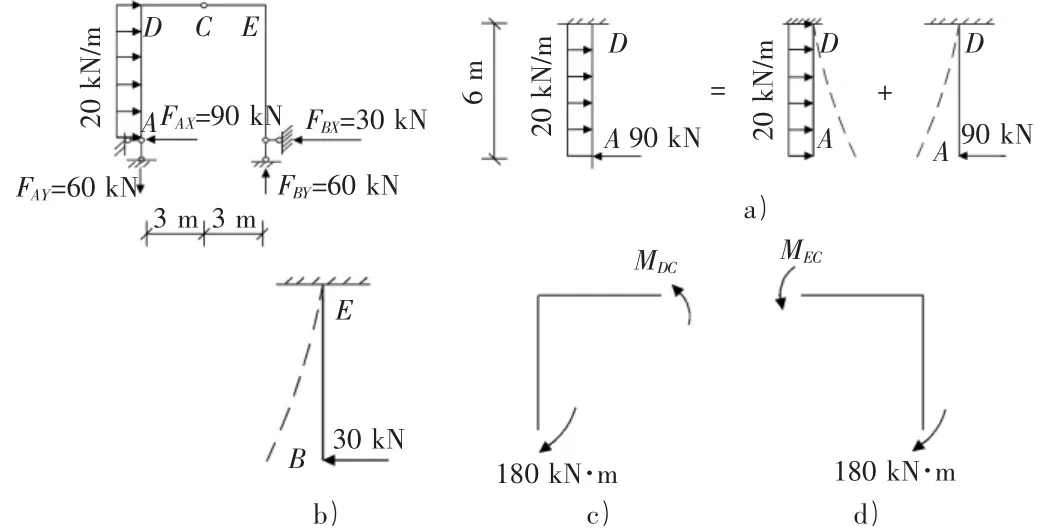
图3 三铰刚架内力分析图
MDA=20×6×3(左拉)-90×6(右拉)= -180 kN·m(右侧受拉)。
MEB=30×6=180 kN·m(右侧受拉)。
根据刚结点D(见图3c))、刚结点E(见图3d))的平衡可得:
MDC=180 kN·m(下侧受拉)。MEC=180 kN·m(上侧受拉)。
根据内力图规律绘出最后弯矩图(见图4)。
3)刚结点弯矩图传递规律。简支刚架或三铰刚架一般先计算竖杆的弯矩,再通过结点的平衡将弯矩传递至横梁。所以如果熟悉刚结点弯矩传递规律,横梁部分不用计算,就可直接得出结果,从而收到事半功倍的效果。
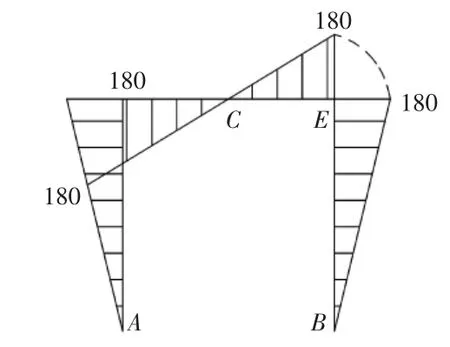
图4 三铰刚架弯矩图(单位:kN·m)
a.两杆刚结。刚结点弯矩可直接传递,受拉侧若一端为内侧,另一端亦为内侧;若一端为外侧,另一端亦为外侧,见图5。b.多杆刚结。杆端弯矩与力偶荷载代数和等于零(半铰接不影响弯矩传递)。
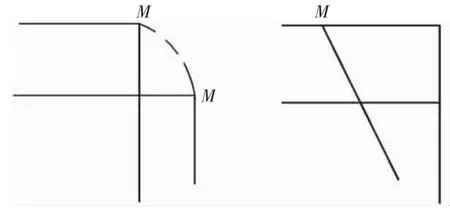
图5 两杆刚结
对于悬臂刚架,如图6所示刚架,可在B,C刚结处将刚架分为AB,BC,CD三段。AB段只要计算出A支座反力偶矩MAB,应用以上方法可快速绘出弯矩图。

图6 多杆刚结
4)铰接点处。铰接点弯矩为零(铰侧有集中力偶作用时,该截面弯矩等于该力偶值)。
3 结语
总结以上作内力图的方法如下:
1)先固定刚结点,以刚结点为界将刚架分解成若干直杆;
2)用规律法计算悬臂直杆部分的杆端内力;
3)利用刚结点的平衡,将结点处的弯矩传递至其余杆端;
4)绘出每段梁的内力图,最后合成为刚架的内力图。
在教学实践中证明只要作一定量的习题练习这种方法很容易被学生掌握。
[1] 陈大堃,沈伦旭.建筑力学[M].上海:高等教育出版社,1990:207.

