平台对门式刚架结构稳定性的影响分析

游 辉 中国寰球工程公司 北京 100012

门式刚架轻型房屋钢结构源于美国 ，经历近百年的发展，目前已成为相对完善的结构体系。门式刚架以其自重轻，耗钢量少，受力简单、传力路径明确，构件制作快捷、施工周期短、可拆迁等优点，现已广泛应用于工业、商业及文化娱乐公共设施等工业与民用建筑中［1-2］。随着门式刚架的广泛应用，衍生出很多新的形式，如带有操作台或局部设置办公室夹层、气楼等。当局部夹层与主体门式刚架共同工作时，就衍生出新的结构形式——带平台门式刚架体系。这种结构体系现已广泛应用于工业和民用建筑，其形式既不同于多层钢结构，也不同于一般的单层门式刚架，形成平台与刚架协同工作的结构体系。由于平台梁约束与竖向荷载的存在，将对刚架的稳定性产生影响。

本文针对一种带平台门式刚架与平台的协同工作，推导了刚架柱稳定计算理论模型，对平台协同工作刚架进行非线性屈曲分析，考察了高跨比、平台梁刚度等因素对平台协同工作刚架稳定性的影响。

1 力学计算模型

图1 给出了普通门式刚架与平台协同工作刚架的计算简图，对比两类刚架可看出，后者平台的刚度与竖向荷载将会影响刚架柱的稳定性。

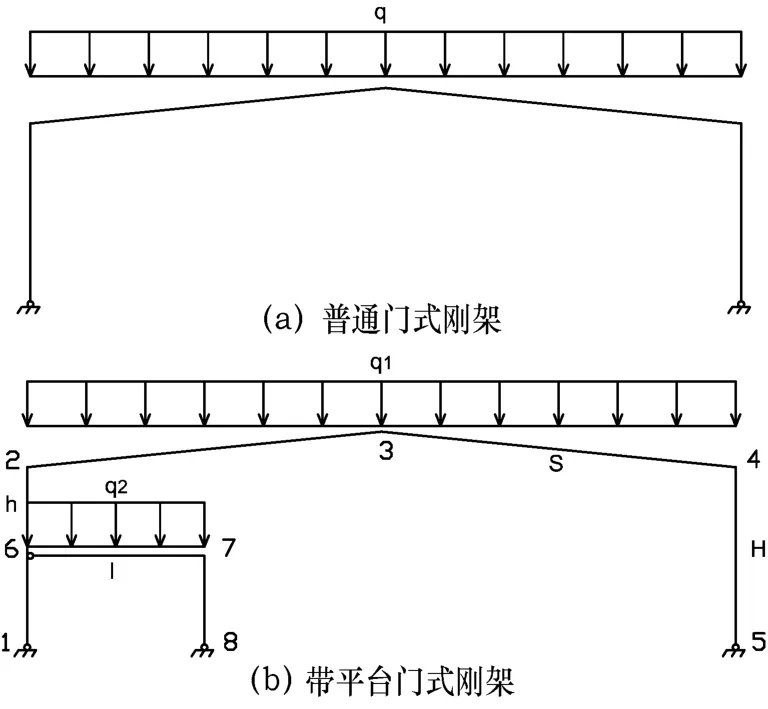
图1 门式刚架计算简图

基于图1 (b)，考虑斜梁荷载和平台竖向均布荷载作用，平台与刚架柱脚均采用铰接，柱高为H，柱的惯性矩为Ic，斜梁长度为S，平台柱高为H-h，平台宽度为L，斜梁和平台惯性矩为Ib，斜梁作用均布荷载q1，平台作用均布荷载q2。门式刚架发生有侧移失稳时，刚架的转角位移关系见图2。其中，刚架的节点2、4、6、7 产生转角θ2、θ4、θ6、θ7和线位移δ2、δ3、δ4、δ6、δ7，考虑刚架的变位曲线可知，线位移δ2=δ3=δ4=Δ2，δ6=δ7=Δ6。

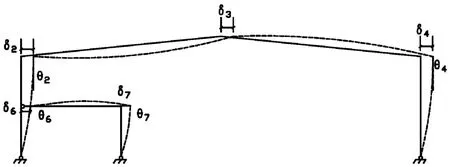
图2 门式刚架的有侧移失稳

根据结构力学、钢结构稳定理论和相关文献3-7 可得到各杆的位移转角方程和节点的平衡方程。

由节点2 的弯矩平衡方程式:

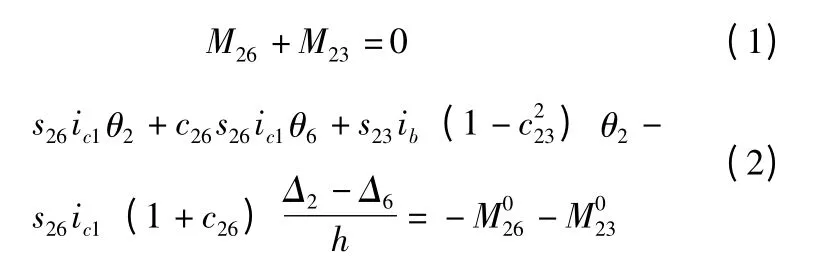
由节点4 的弯矩平衡方程式:

由节点6 的弯矩平衡方程式:

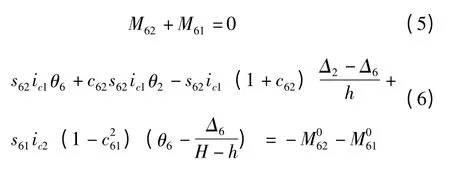
由节点7 的弯矩平衡方程式:

利用剪力平衡条件:

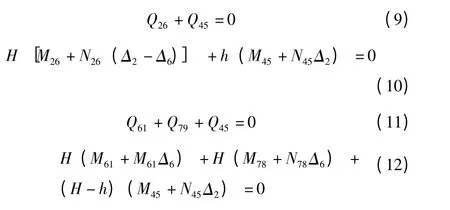
各式联立，写成矩阵形:

在弹性范围内，山形门式刚架的临界荷载与非齐次项无关，可以用求特征值的方法求得临界荷载，即令系数矩阵的行列式等于零。显然u23=u43，u26=u62。行列式化为:

通过上述公式可利用数学分析软件进行求解，分析门式刚架柱的稳定性。

2 数值模拟

基于理论分析，对平台协同工作刚架进行非线性稳定分析。门式刚架计算模型见图3。

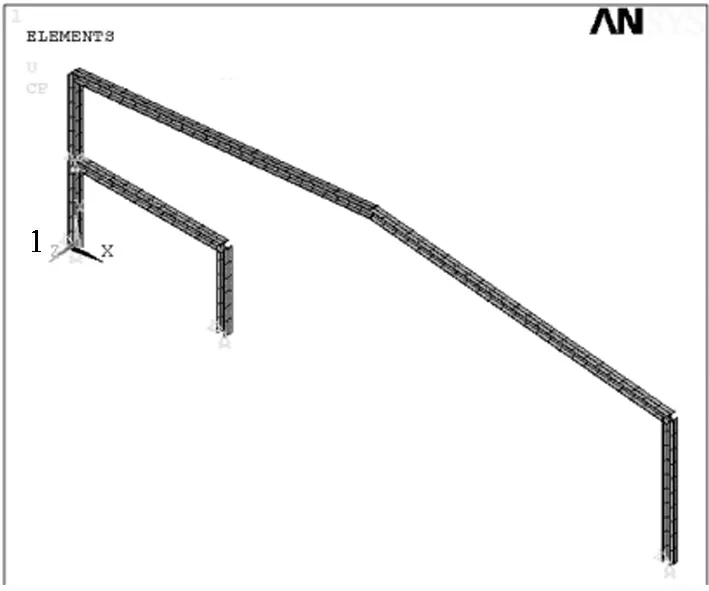
图3 计算模型

其中刚架跨lb=24m，柱高H =6m，平台宽度L=6m，平台柱高H - h =3m，刚架梁坡度为1:10，斜梁长度S =1.2。梁柱采用等截面的工字型截面，柱的截面尺为H300 ×300 ×12 ×20，梁的截面尺寸为H300 × 300 × 12 × 20，所有钢材均为Q345 钢，其弹性模量E=2.06 ×1011N/m2。柱脚铰接，荷载为竖向均布荷载，屋面荷载q1=1.6kN/m，平台载荷q2=12kN/m。

分析中需考虑在刚架失稳过程中平台对刚架结构的影响。采用弧长法迭代技术，可以得到刚架失稳时柱脚反力-位移全过程变化曲线以确定刚架柱的极限荷载。单元采用Beam189，该单元能考虑大转动、大应变等几何非线性问题。为保证刚架平面外稳定，在梁、柱和工作平台的端部、跨中均设侧向支撑。

图4 为平台协同工作刚架特征值屈曲分析一阶模态图，其特征值屈曲系数为64.811，刚架柱极限荷载FN=1325.38kN。从图中可看出一阶模态为有侧移失稳。算例模型高跨比为1:4，其分析结果与文献［8］结论一致，即当刚架高跨比大于等于1:5 时，刚架失稳形式为有侧移失稳。

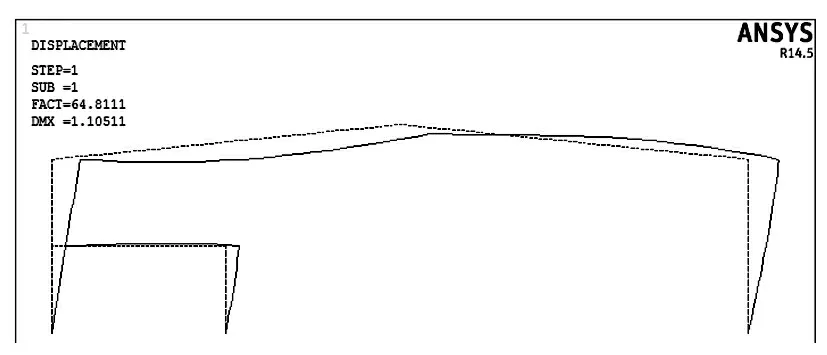
图4 刚架一阶屈曲模态

由于特征值屈曲分析只能得到临界荷载和相应的失稳模态，对结构临界失稳力的预测往往也高于结构实际的临界失稳力，而非线性屈曲分析通常比特征值屈曲分析更符合实际情况，故实际工程上常用非线性屈曲分析结果来进行结构设计。

图5 为平台协同工作刚架跨中节点荷载-竖向位移曲线，极限荷载FN=222.4kN。当荷载较小时，跨中节点竖向位移和荷载呈线性，随着荷载的增加，位移增加的速度减慢。当荷载到某一定值时，荷载小幅增加，位移大幅增长，此荷载即为刚架的临界荷载。

图5 跨中节点荷载-位移曲线

相对于一般的轻型门式刚架，平台协同工作刚架的平台自重与使用荷载均较大，不能忽略平台结构对刚架整体结构的影响。图6 给出了普通门式刚架柱与平台协同工作刚架柱荷载-位移曲线对比。

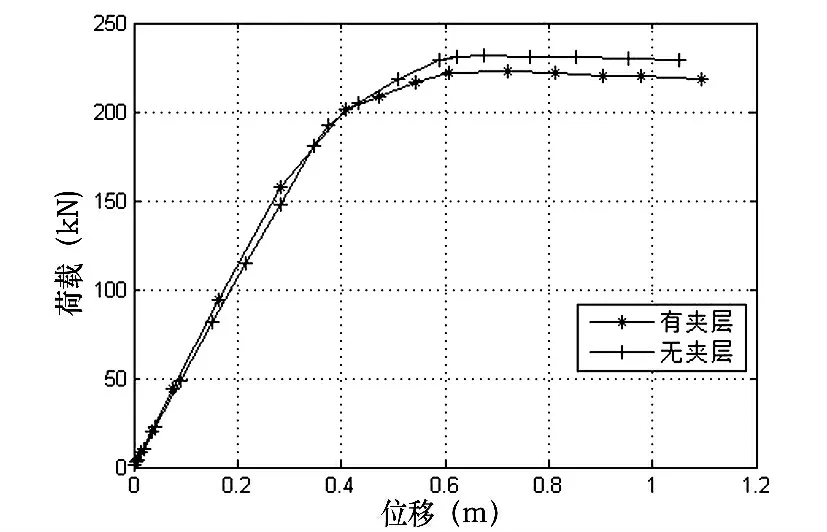
图6 带无平台门式刚架荷载-位移曲线

从图6 可看出，加载初期，两类刚架的位移都随着荷载的增大呈线性变化，当荷载增大到一定值时，分别进入失稳状态。由于平台梁刚度和平台荷载等因素影响，平台协同工作刚架失稳时位移和极限承载力都有所增大。本算例普通单层门式刚架的极限承载力约为218.6kN，平台协同工作刚架的极限承载力约为222.4kN。

图7 给出了柱底铰接和柱底刚接的两类刚架的荷载-位移曲线对比。从图7 可见，柱底刚接的平台协同工作刚架的极限承载力为257.2kN，柱底铰接极限承载力为222.4kN。柱底刚接的刚架柱极限承载力明显大于柱底铰接刚架柱，两者相差近13%。这是由于柱底刚接使得刚架柱底可以传递弯矩，刚架整体所受弯矩更加均匀，提高了刚架的承载能力。

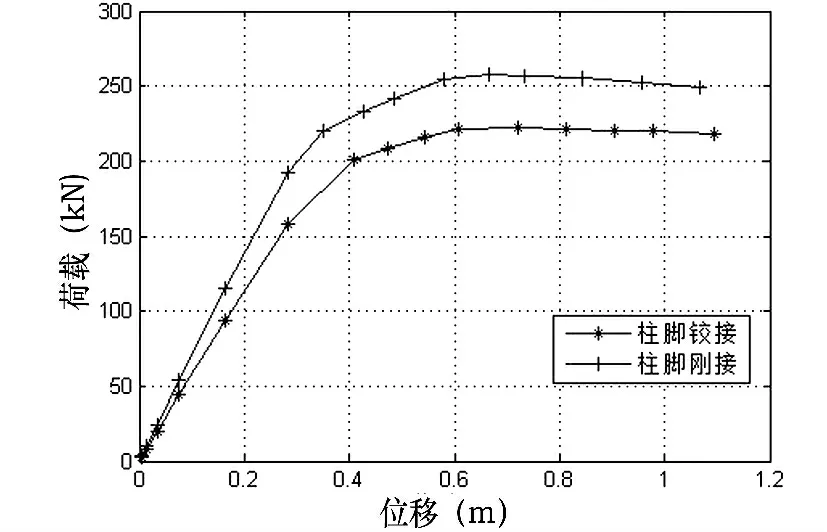
图7 柱底铰接和柱底刚接平台协同工作刚架荷载-位移曲线

3 参数分析

3.1 高跨比对平台协同工作刚架的影响

高跨比是影响门式刚架极限承载力的重要因素。考虑平台对刚架柱的影响，保持跨度和平台柱高度不变，通过调整刚架柱高度来改变高跨比。

图8 和图9 给出了高跨比对平台协同工作刚架的荷载位移曲线及承载力关系曲线。从图8 和图9中可看出，高跨比越大，平台协同工作刚架的极限承载力越小，但高跨比越大，刚架失稳时的位移越大。

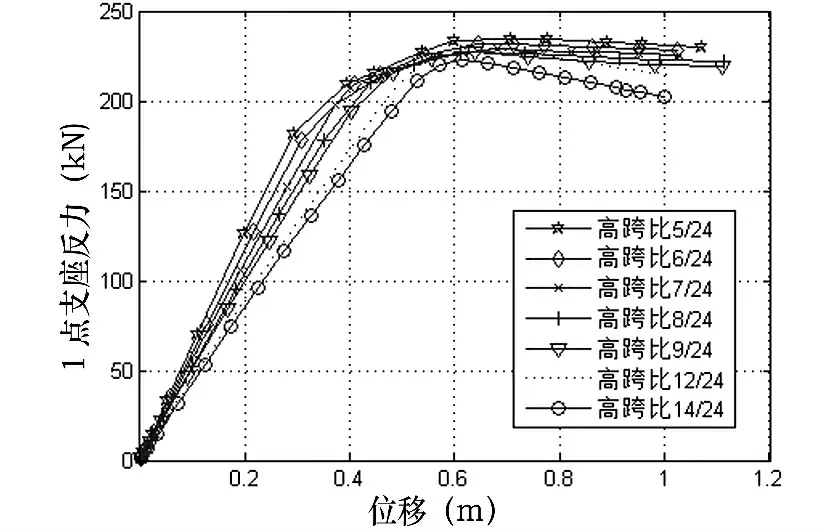
图8 不同高跨比平台协同工作刚架荷载-位移曲线

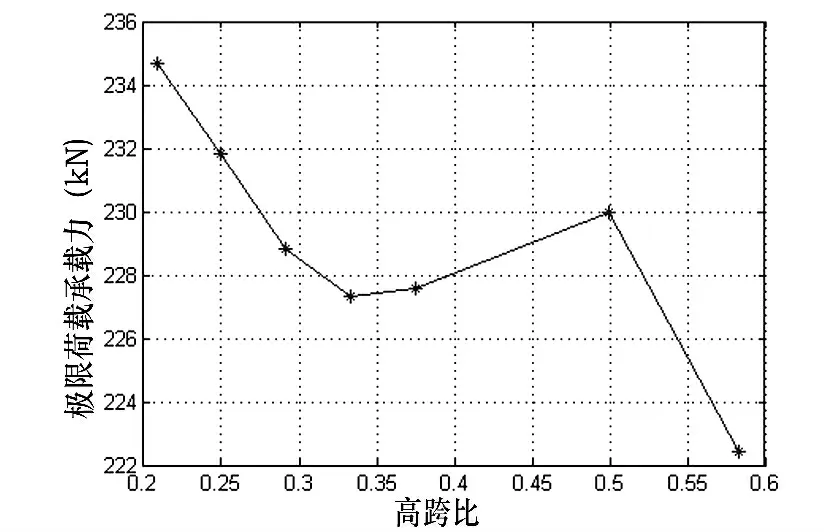
图9 高跨比与极限承载力关系变化曲线

3.2 平台刚度对门式刚架稳定性的影响

保持门式刚架主体结构不变，改变平台的宽度(分别取2m、4m、6m、8m、10m)，通过对不同平台宽度的平台协同工作刚架进行非线性分析，找到不同宽度的平台对有平台门式刚架的影响。此情况下平台协同工作刚架荷载-位移曲线和不同宽度平台与极限承载力的变化规律曲线见图10和图11。

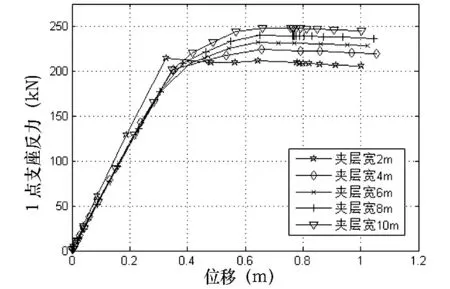
图10 不同平台宽度的平台协同工作刚架荷载-位移曲线

图11 平台协同工作刚架极限承载力随平台宽度变化曲线

从图10 可见，随着平台宽度的增加，平台协同工作刚架极限承载力呈上升趋势。屈服前，各宽度的平台协同工作刚架极限承载力变化情况相似，曲线基本重合;失稳后，曲线分散，平台宽度大的刚架曲线变化幅度大，平台宽度小的刚架曲线变化幅度小。平台承受很大荷载，增大平台宽度使得平台承受更大的水平荷载，增强了刚架柱的抗侧刚度，也就提高了其极限承载能力。从图11 可看出，刚架的极限承载力随着平台宽度的增加基本呈线性变化。

4 结语

由于增设局部工作平台，使得原有门式刚架结构体系的受力状态和结构承载力发生了一些变化，主要影响:

(1)增设工作平台能够提高刚架柱的抗侧刚度，提高刚架整体的承载力。

(2)刚架的极限承载力随平台协同工作刚架的高跨比的增加而降低，但刚架失稳时位移增大。

(3)刚架失稳前，平台梁刚度和平台荷载对平台协同工作刚架没有影响，失稳后刚架承载力随平台梁刚度增加而增大。

1 于荣俊，彭宣茂，彭新宣. 带复杂夹层门式刚架设计［J］.工业建筑，2012，42 (2):144 -146.

2 李雄彦，徐兆熙，薛素铎. 门式刚架轻型钢结构工程设计与实例［M］. 北京:中国建筑工业出版社，2008.

3 李廉锟. 结构力学［M］. 北京:高等教育出版社，2000.

4 陈 骥. 钢结构稳定理论与设计［M］. 北京:科学出版社，2003.

5 陆 鑫. 轻型钢结构厂房门式刚架的弹性对称失稳分析［D］. 浙江:浙江大学，2000.

6 Mansur，E. F. Chang，I. C. Donnell，L. H. Stability of Frames in The Presence of Primary Bending Moments. Journal of Engineering Mechnics. Div. ASCE，87 (4):19 -34.

7 丁洁民，沈祖炎. 多层及高层钢刚架的弹塑性稳定［J］.同济大学学报，1989，17 (2):149 -160.

8 文 峰，王海忠. 山形门式刚架的整体稳定分析［J］. 工程建设与设计，2006，2:12 -15.