基于模糊控制理论的船舶动力定位系统的研究
郭 敏
(武汉船舶职业技术学院动力工程学院,湖北武汉 430050)
依靠船舶推进系统用于保持船舶在水平面上的跟踪预定航迹或者艏向角和固定的位置称为船舶的动力定位(Dynamic Positioning,简称DP)系统[1]。其基本工作原理是,先通过各种传感器实时地检测出船舶的实际位置并与目标位置作比较得出偏差值,然后把偏差值信号送给控制器,控制器则根据风、浪、流等外界扰动力进行计算,得出使船舶恢复到初始设置的目标位置需要多大的推力,最后控制器还要对船舶上各推力器进行推力分配并发出推力指令给执行机构(即推力器),从而使船舶恢复到初始设置的目标位置[2]。
早期动力定位控制系统常采用的是带有陷波滤波器或低通滤波器PID方法和基于线性最优随机控制理论的LQG方法。由于PID控制存在误差信号相位滞后,控制参数难以整定和事后控制等缺点,且LQG控制虽然在安全、节能以及鲁棒性能上都有了较大的进步,其响应速度和控制精度满足了动力定位船舶的大部分要求。但船舶定位的过程是一个复杂的高度非线性的过程,在设计LGQ控制器的过程中对系统模型进行线性化处理,这种处理方法会产生较大的计算量并存在误差。
从20世纪70年代开始,模糊控制理论在短短几十年取得很大的发展,它利用多值模糊逻辑和人工智能要素(简化推理原则)来模仿人的思维及反应,它是一种智能的控制方法。模糊控制不需要知道控制对象的精确数学模型,它的特点是具有很强的抗干扰能力、鲁棒性好以及响应速度快等。由此可见,在动力定位船舶中使用模糊控制技术是非常合适的。
1 船舶动力定位系统数学模型
1.1 低频船舶动力模型
在船舶动力定位控制系统设计过程中,一般考虑低速船舶纵荡、横荡和艏摇3自由度的低频运动模型,根据现代控制理论中状态空间的概念,动力定位船舶中简单化的船舶低频运动模型可以表示为:

式中,η=[x,y,ψ]T∈R3分别表示船舶相对基准点在x,y方向上的距离,以及艏向角度;位置向量v=[u,v,r]T为相应的x、y方向上随船速度、角速度向量为大地坐标和船体坐标系间的转换矩阵;M=为质量矩阵,它包含了水动力附加质量;D=为阻尼矩阵;为线性项,一般情况下可用来表示辅助锚泊系统产生的力和力矩。在动力定位系统中没有采用辅助锚泊系统时[6],K=0;τ=[τ1,τ2,τ3]T∈R3分别表示x、y方向上的推进力,和推进器以及舵产生的转艏力矩。
1.2 环境扰动力模型
船舶在海上动力定位时,会受到海浪和海风及海流的扰动,这些会使船位和艏向发生变化。常风的风力、海流的作用力和波浪力的经验公式为[7];

式中,ρa为空气密度,Af为水线以上船舶正投影面积,Va为风速,As为水线以上船舶侧投影面积,α为风舷角,L为船长,CXa,CYa,CNa为风力系数,是关于风舷角的α函数。

这里,AFW为水线面以下船舶正投影面积,VC为流速,ASW为水线面以下船舶侧投影面积,β为流的入射角,CX(β),CY(β),CN(β)为实验系数,也可用下式求取
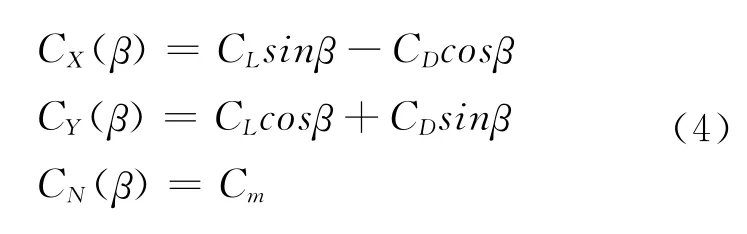
式中,,,分别作为短翼的船体升力系数、阻力系数和转矩系数。
借助于Excel的规划求解,在设定目标利润480千元以及维持固定成本和销量的情况下,新模式下单价和单位变动成本还可以分别下降0.1%和1.7%,较之旧模式依赖于单价提高0.7%,明显有很大进步。因此,新模式下,在增加投资、降低材料和直接人力成本是有保障的,风险低于旧模式。

其中,ζD为平均波浪幅值,g为重力加速度,ψ为艏向,θD为波浪方向,CXD,CYD,CND为波浪漂移力系数,该系数可用以下回归公式计算:

1.3 测量系统的模型
船舶动力定位的艏摇角度和位置通常通过陀螺仪、水声定位系统或者差分GPS等测量系统获得。其测量值可以写为:

其中,η为低频运动位置;ηw为高频运动位置;为零均值测量高斯白噪声。
2 船舶定位系统模糊控制器的设计
由于模糊控制是以模糊逻辑、模糊集合论、模糊语言变量以及模糊推理为基础的一种非线性的计算机数字控制技术。因此,动力定位船舶的模糊控制系统的组成类同于一般的数字控制系统[8],其结构方框图如图1所示。

图1 模糊控制系统结构框图
为了表示方便,我们把该状态空间模型变形可得如下状态空间模型[9]:

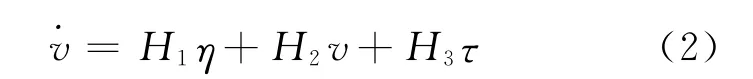
其中,H1=-M-1K为船舶相对于静坐标系中位置和艏摇角度ψ的状态矩阵,H2=-M-1D表示纵荡,横荡,艏摇速度的状态矩阵,H3=-M-1表示控制力、力矩的状态矩阵。
规则2:如果:接近

规则3:x3如果:接近

T-S型模糊控制模型可以表示为:

其中 Mij(zj(t))表示 Mjzj(t)隶属于模糊集合Mij的隶属度。ωi(z(t))为第i条模糊规则的权重(即第i条模糊规则在总输出中所占分量轻重的比例)。本文中动力定位船舶系统的T-S型模糊控制隶属函数如下图:
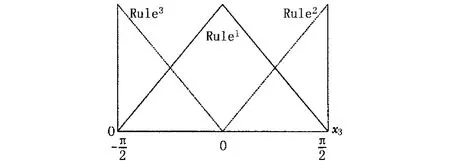
图2 x3(t)的隶属函数混合灵敏度设计问题
3 仿真分析
所选择实验船的船长为75.2m,船高4.5m,船宽10m。则其质量阵和阻尼阵为: 它的惯性项、阻尼项矩阵如下:
惯性项矩阵为:

阻尼项矩阵为:

辅助锚泊系统产生的力和力矩:

运用Matlab中的LMI工具箱求解凸优化问题,可以得到如下结果[10]:

由计算结果,可以找到P>0,模糊控制器可以表示为:
u(t)=h1(z(t))G1x(t)+h2(z(t))G2x(t)+h3(z(t))G3x(t)其输入为船舶相对基准点的位置和艏摇角度以及三个方向上的速度、角速度,输出为保持定位所需的x、y方向的推力和转艏力矩。
运用Matlab中的模糊工具箱,得仿真结果如下

图3 艏摇角度
图4 X方向速度

图5 Y方向速度

图6 角速度

图7 XY位移
4 结 论
从仿真结果可以看出,基于模糊控制理论设计的船舶定位控制系统的响应时间、上升时间较快,超调率低,具有一定的抗干扰能力,有较强的鲁棒性,具有良好的控制品质。这种方法较好地解决了动力定位船舶控制系统设计中存在的船舶模型参数不确定时的低频位置、速度、高频位置以及环境干扰力的估计问题。
1PhillipsDF.TheDynamicPositioningofShips;The ProblemsSolved[C]//UKACCInternationalConferenceon CON-TROL’96.London:TheInstitutionofElectrical Engineers,1996:1214-1219.
2A.Lough.DynamicPositioning.Lioyd’sRegisterTechnical Association.1985.
3Fossen,ThorI.GuidanceandControlofOceanVehicles.ChichesterNewYork,1994.
4AntonioLoria.SeparationPrincipleforDynamicPositioningofShips:TheoreticalandExperimentalResults.IEEE TRANSACTIONONCONTROLSYSTEMSTECHNOLOGY,VOL.8,NO.2,MARCH2000.
5LoriaA,FossenTI,PanteleyE.ASeparationPrinciple forDynamicPositioningofShips:TheoreticalandExperimentalResults[J].IEEETransactionsonControlSystems Technology,2000,8(2):332-343.
6 童进军,何黎明,田作华.船舶动力定位系统的数学模型.船舶工程,2002(5)27-29.
7IsherwoodRM.Windresistanceofmerchantship[J].TransactionoftheRoyalInstitutionofNavalArchitects(S0035-8967),1972,115;327-338.
8 赵志高.动力定位控制系统的设计和研计.上海交通大学硕士学位论文.2002.02.
9W.-J.Chang,G.-J.Chen,Y.-L.Yeh,Fuzzycontrol ofdynamicpositioningofships,J.Mar.Sci.Technol.10(2002)47–53.
10 刘叔军,盖晓华,樊京等.Matlab7.0控制系统应用与实例.北京:机械工业出版社,2006

