大型桥式起重机承轨梁结构模态分析

戢 平，郭 燕

(武汉理工大学物流工程学院，湖北 武汉 430063)

桥式起重机频繁吊装作业所产生的振动对整个承轨梁的疲劳寿命会产生很大的影响，造成承轨梁结构的疲劳破坏、共振和噪声。当承轨梁所受激振力的频率与其自身结构的某一固有频率接近时，就有可能引起结构共振，从而产生很大的动应力，对结构的强度造成破坏或产生大变形而影响承轨梁的性能[1－5]。因此，在承轨梁结构的静强度、刚度和整体稳定性满足设计要求后，分析承轨梁的模态是有必要的。为此笔者应用ANSYS软件对250 t桥式起重机承轨梁结构的模态进行详细分析。

1 模态分析基本理论

结构模态分析的目的是识别结构的模态参数，得到结构的动态特性，为解决各类工程动力学问题提供依据[6]。任何结构或部件都有固有频率和相应的模态振型，这是结构或部件自身的固有属性[7]。典型的无阻尼结构自由振动的运动方程为:

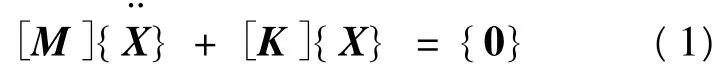
如果结构以某一固有频率和模式振动，即:

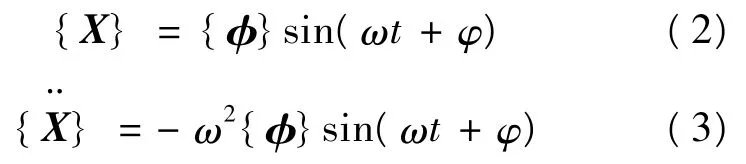
将其代入运动方程，可得结构自由振动特征方程:

欲得非零解，必须满足:

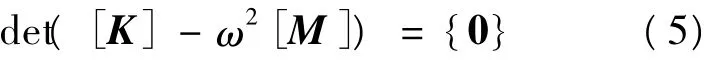
式(5)称为结构振动的特征值方程，该方程的特征值为ω2i，回代到特征方程，可得到特征值对应的特征向量{φi}。特征值的平方根ωi为结构的自振圆频率，特征向量{φi}为结构对应于ωi的振型向量。

通过ANSYS模态分析可以确定部件的频率响应和模态。对于动力加载下的结构设计而言，频率响应和模态是非常重要的参数。

2 桥式起重机承轨梁

以某厂自用重件码头上的250 t桥式起重机承轨梁为研究对象，它采用斜拉杆和桁梁混合结构型式。主梁与立柱通过4根斜拉杆(两侧共8根)连接，两侧主梁、立柱通过平联桁架连接，在岸侧有4座岸侧支座，在水侧有4座水平侧向支座及两座桥墩，承轨梁结构布置图如图1(a)所示，其中主梁、拉杆和立柱等主要截面的几何参数如图1(b)所示。

3 模态计算及其结果分析

一个典型的模态分析过程主要包括建模、模态求解、扩展模态、观察结果，以及结果分析5个步骤，结合以上5个步骤，对承轨梁结构的模态进行详细分析。

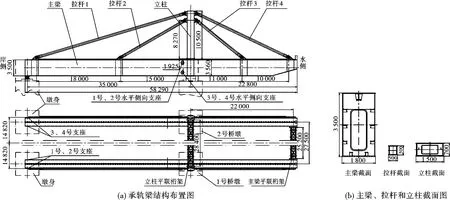
图1 承轨梁结构布置图

3.1 桥式起重机承轨梁的模型

在ANSYS中建立桥式起重机承轨梁的有限元模型，承轨梁的主梁、立柱、拉杆和支座都是用钢板焊接而成，故采用板单元SHELL63建模，立柱平联桁架和主梁平联桁架采用BEAM188建模。材料的弹性模量EX=2.1×105MPa，泊松比PRXY=0.3，密度 ρ=7.85 ×103kg/m3[8－10]。模型建立后，采用自由划分网格，共划分33 603个板单元和256个梁单元，节点33 935个，总质量约622 700 kg。承轨梁结构的有限元模型如图2所示。

图2 承轨梁结构有限元模型

3.2 模态求解

3.2.1 模态分析的求解设置

将ANSYS求解器的分析类型设置为Model。该模型选择提取模态方法MODOPT区域中的Block Lanczos，该方法求解精度高，计算速度快。设置提取模态阶数为10，扩展模态阶数为10，模态提取频率的范围FREQB=0，FREQE=100 000。

3.2.2 设定边界条件

在典型的模态分析中唯一有效的载荷是零位移约束。如果在某个DOF处指定了一个非零位移约束，程序将以零位移约束代替在该DOF处的设置。在承轨梁模型中，主要的约束是:岸侧墩柱1～4号支座底板的全部约束;水侧墩柱1～4号水平侧向支座底板的全部约束;水侧墩柱的1号和2号桥墩在装橡胶支座处约束承轨梁结构的铅垂方向位移(Y方向自由度)和沿小车(250 t桥式起重机)运行方向位移(Z方向自由度)。

3.2.3 模型求解

求解器的输出内容主要是固有频率，固有频率被写到输出文件Jobname.OUT及振型文件Jobname.MODE中。

3.3 扩展模态及其求解

模态求解完成后，模态振型被写入结果文件，此时可以通过后处理器POST1观察结构的模态振型。在观察特定振型中的相对应变和应力等派生数据时，需要扩展模态[11]。每一次扩展处理的结果文件存储为一个单独的载荷步。扩展处理的输出包括已扩展的模态振型和各阶模态的相对应力分布。

3.4 观察结果

模态分析的结果写入在分析结果文件Jobname.RST中，分析结果包括固有频率、振型以及相对应力分布等。一般在通用后处理器POST1中观察模态分析的结果。

通过对该承轨梁结构模态求解，可获取其前10阶模态参数和固有频率，以及振型图。承轨梁结构的前10阶模态分析结果如表1所示。

承轨梁结构振型图如图3～图12所示。

3.5 模态结果分析

(1)从承轨梁固有频率的计算结果可以看出，第2、3阶，第5、6阶模态的频率相近，这是由于承轨梁结构对称造成的。

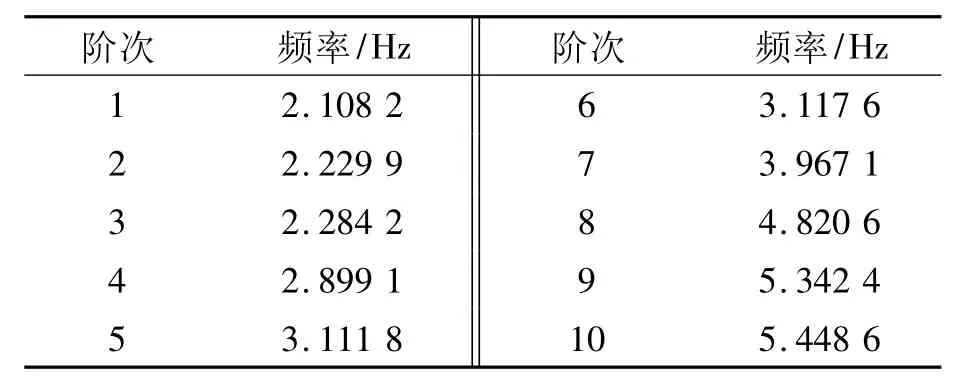
表1 整机前10阶模态分析结果

(2)桥式起重机在加载、卸载时，承轨梁在垂直方向将产生衰减振动。这种振动对结构强度的影响不大，但在频率过大时对桥式起重机的正常使用以及司机的操作不利，且缓慢的衰减过程会影响桥式起重机的生产率。根据机械振动理论，低阶固有频率的振动是振动过程中对结构起主要作用的因素，而较高频率的振动对结构的影响作用较小，且高频振动也会因为系统中的阻尼特性而在一般情况下很快衰减。

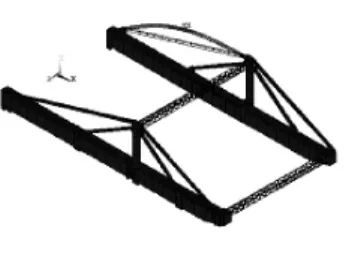
图3 第1阶振型

图4 第2阶振型

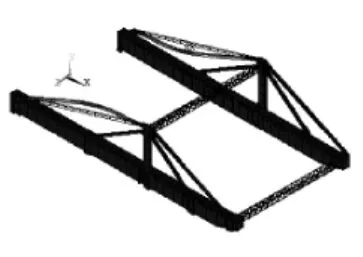
图5 第3阶振型

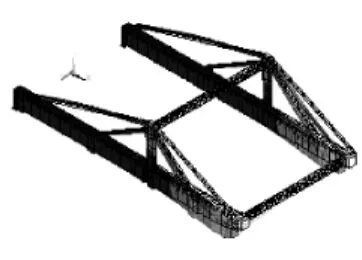
图6 第4阶振型

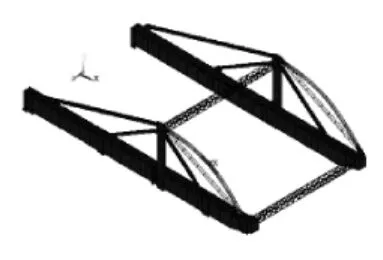
图7 第5阶振型

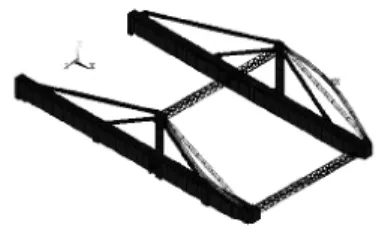
图8 第6阶振型

图9 第7阶振型

图10 第8阶振型

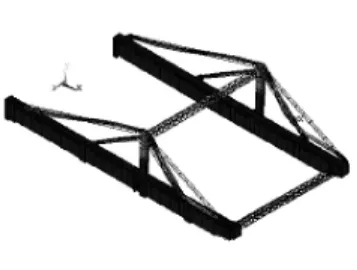
图11 第9阶振型

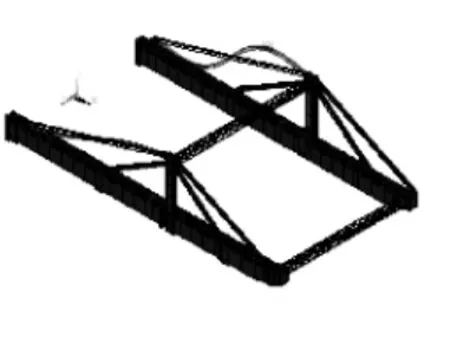
图12 第10阶振型

表1中数据表明，当外部激励频率接近表中的数值时，模型将可能产生较大振动，破坏结构性能。从承轨梁模态分析的结果可知，第1阶固有频率为2.108 2 Hz，满足GB/T 14406－1993龙门起重机动态刚性的规定:当小车位于跨中时，主梁的满载自振频率应不小于2 Hz。

(3)第1、2、3阶固有振型反映了承轨梁拉杆1的垂直振动，第5、6、8阶固有振型反映了承轨梁拉杆4的垂直振动，它们可由桥式起重机启动、制动等原因激励引起;第4、7、9阶固有频率分别反映了主梁和立柱的水平振动，拉杆1和拉杆4的水平振动及垂直振动是由桥式起重机的大车、小车联合动作引起;第10阶固有频率反映了承轨梁拉杆1的复杂变形，它可由桥式起重机上小车的起、制动等原因激励引起。图13的频率曲线清楚地反映了承轨梁固有频率的走势，对大型承轨梁的设计具有一定的参考价值，同时也为其虚拟样机的设计和动力学仿真提供了依据。

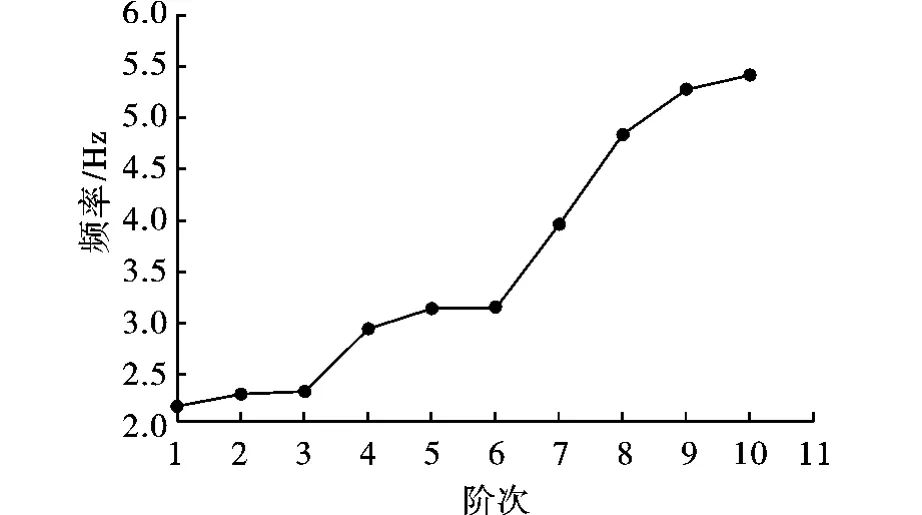
图13 频率阶次曲线

4 结论

利用ANSYS软件对250 t桥式起重机承轨梁进行模态分析，得到承轨梁的前10阶固有频率和振型。该模态分析为大型承轨梁的设计提供了理论依据，同时也为承轨梁的动力学分析提供了宝贵的参考价值。

[1] 王金诺.起重机械金属结构[M].北京:中国铁道出版社，2002:12－98.

[2] 张志文.起重机设计手册[M].北京:中国铁道出版社，2001:80－121.

[3] GB3811－2008，起重机设计规范[S].

[4] 交通部水运司.港口起重运输机械设计手册[M].北京:人民交通出版社，2001:95－98.

[5] 上海港机重工有限公司.港口起重机设计规范[M].北京:人民交通出版社，2008:34－97.

[6] 宋勇，艾宴清，梁波，等.精通ANSYS7.0有限元分析[M].北京:清华大学出版社，2003:23－65.

[7] 尚晓江.ANSYS结构有限元高级分析方法与范例应用[M].北京:中国水利水电出版社，2006:65－132.

[8] 李拔周，徐长生.基于ANSYS的100 t龙门起重机结构有限元分析[J].起重运输机械，2007(3):12－14.

[9] 计三友，苏运波.龙门起重机结构模态分析[J].起重运输机械，2007(9):57－59.

[10] 李端，徐长生.门座起重机四连杆组合臂架结构的动力学分析及仿真[J].武汉理工大学学报，2005，29(1):94－96.

[11] 肖博，郭建生.基于多体分析的四连杆臂架系统变幅过程研究[J].武汉理工大学学报:信息与管理工程版，2010，32(1):74 －77.