基于支持向量机的磁力轴承系统辨识研究

苏义鑫，张 丽，蓝 天

(1.武汉理工大学自动化学院，湖北 武汉 430070;2.华中科技大学电气与电子工程学院，湖北 武汉 430074)

磁力轴承是典型的机电一体化非线性系统，动态性能较复杂。一般在平衡点附近进行线性化处理，然后再根据线性化系统的方法设计控制器[1－2]。传统的系统辨识方法是通过建立对象的参数模型，把辨识问题转化为参数的估计问题。这类算法成功地应用于线性系统或可线性化系统的辨识。文献[3]的递推最小二乘估计算法、文献[4]的单纯形法都是将磁力轴承模型线性化，得出依赖于参数的二阶模型，然后由实际系统的输入输出数据辨识出该模型的参数。但线性化模型与实际模型存在误差，当转子大范围工作时，可能导致控制失败。针对该问题，将神经网络技术应用于磁力轴承系统辨识与控制，文献[5]和文献[6]采用BP算法对磁力轴承系统进行辨识，取得了不错的效果。但神经网络仍有一些不易解决的难题，如隐层节点数的选择、过学习和训练过程中存在局部极小等。

从理论上讲，支持向量机因采用了二次规划寻优，故可以得到全局最优解，解决了在神经网络中无法避免的局部极小问题;由于采用了核函数，巧妙解决了维数问题，使得算法复杂度与样本维数无关，非常适合于处理非线性问题[7－9];另外，支持向量机应用了结构风险最小化原则，具有非常好的推广能力。因此，笔者采用支持向量机回归理论对系统的非线性模型进行辨识。通过对磁力轴承系统的仿真实验，验证了该方法的有效性，为磁力轴承控制器的设计打下基础。

1 支持向量机回归原理

1.1 支持向量机回归算法

支持向量机是VAPNIK提出的一种基于统计学习和结构风险最小化原理的新型学习机[10]。其基本思想是基于最小化VC维的上界来控制用于拟合函数的样本容量，具有良好的泛化能力。假设辨识系统的输入输出样本集为:

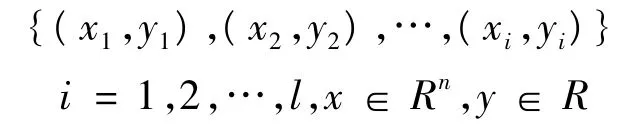
回归问题就是求取一个回归函数:

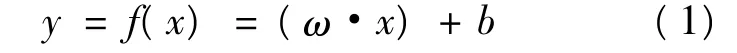
使得对于任何输入x，都能够在精度范围内找到对应的输出y。并且满足期望风险函数最小，即:

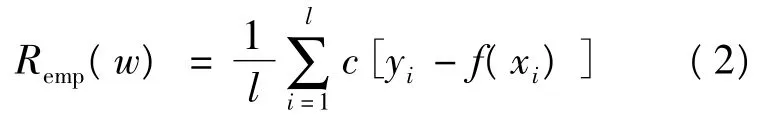
其中，c(·)为损失函数。笔者采用ε不敏感损失函数。

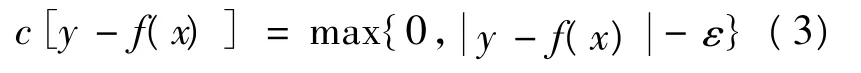
它意味着不惩罚偏差小于ε的误差项，可以增加回归的鲁棒性。回归问题可以转化为最优化问题，利用拉格朗日函数和对偶定理[11]可以得到对偶问题:

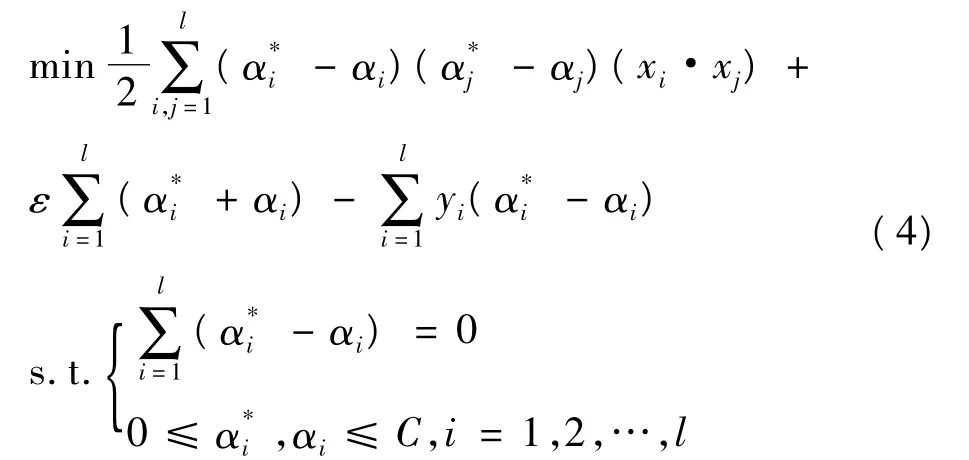
这里C为惩罚系数，ε为不敏感系数。该问题是凸二次规划问题，设是式(4)的任意解，若α*中有取值在开区间(0，C)的分量，根据α*的值可以计算出(ω，b)的解。故可求出回归函数:

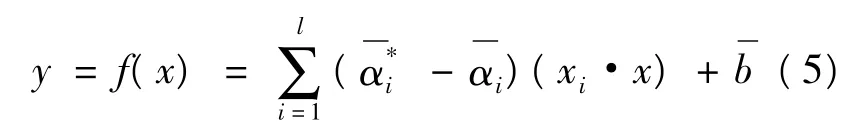
对于非线性问题，首先利用一个非线性映射Φ把训练数据映射到一个高维特征空间H，然后在这个空间建立一个线性回归函数，即:

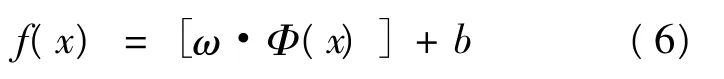
经过推导，变换Φ在算法中的作用可通过内积来实现。故可采用核函数计算特征空间的内积:

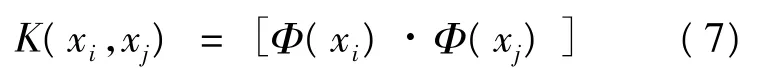
目前，核函数及其参数的选择大都根据经验来选取。最常使用的核函数有以下几种:

(1)d阶多项式核函数:

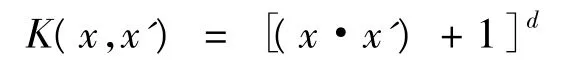
(2)径向基核函数:

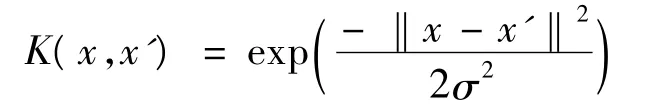
(3)Sigmoid核函数:

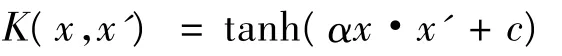
故非线性回归函数可以表示为:

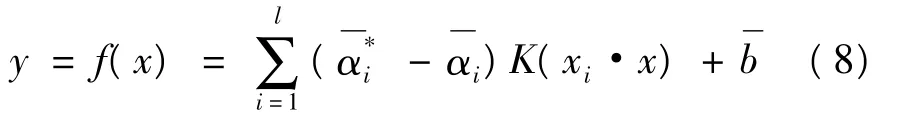
支持向量机在形式上与神经网络非常相似，它的输出是若干个中间层节点的线性组合，而每个中间层节点对应于一个输入样本和一个支持向量的内积。支持向量机示意图如图1所示。

1.2 支持向量机系统辨识原理

由于被控对象的数学模型未知，必须根据被控对象的输入输出数据集，用SVM来对其动态行为建模。通常，离散系统第k+1时刻的输出可表示为之前n个输出和m个输入的函数，即:

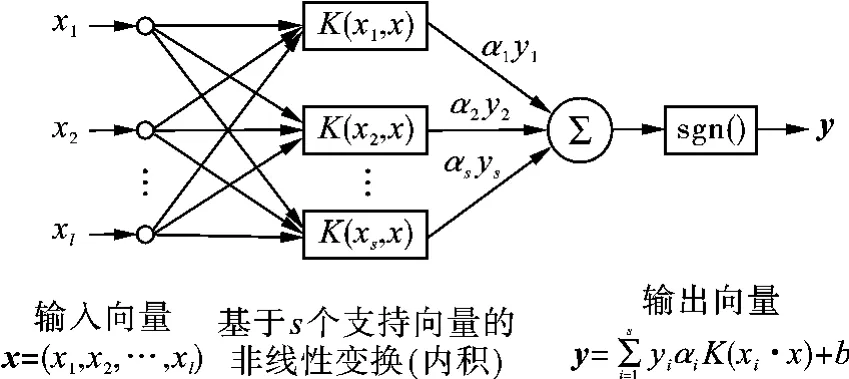
图1 支持向量机示意图

其中，拟合因子 x(k)=[y(k)，…，y(k－n+1);u(k)，…，u(k－m+1)]T，x∈Rm+n;在第 k+1时刻，SVM给出y(k+1)的估计值:为设计SVM辨识器，首先建立训练样本集T:

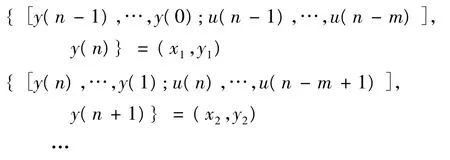
然后确定SVM中的核函数和惩罚参数。用样本集T来训练SVM。训练后的SVM模块可作为模型来描述被控系统的动力学行为。

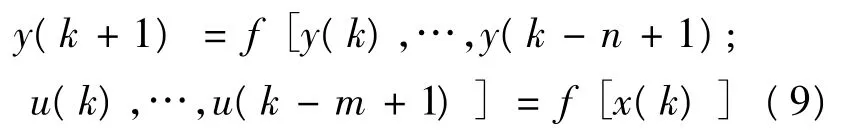
2 磁力轴承系统辨识仿真

2.1 磁力轴承的数学模型

一个单自由度磁力轴承系统的组成及功能如图2所示。系统主要由电磁铁、转子、转子位置传感器、位置控制器和功率放大器几个部分组成。转子在任一时刻的位置信号都由位移传感器获得，这个信号经过相应的前置处理后送到控制器，同时与设定的信号比较后产生误差信号，该误差信号经过控制理论或给定的控制策略变成矫正信号，再通过功率放大器放大后变成足够的电流或电压输出，以驱动电磁铁产生相应的恢复力，使转子重新回到平衡位置，从而实现转子在无接触状态下的稳定悬浮。通常，每个自由度有一对电磁铁在工作，采用差动工作方式，一个磁极对以偏置电流i0与控制电流i之和(i0+i)激磁，而另一个则利用二者之差(i0－i)激磁。改变控制电流，则可改变两个电磁铁产生的吸引力大小，使转子稳定地悬浮在平衡位置。

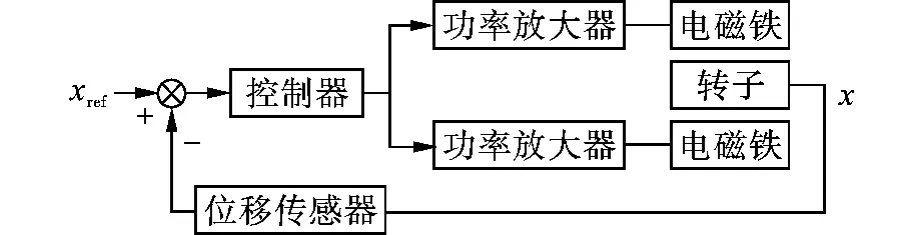
图2 单自由度磁力轴承组成及功能简图

理论证明磁力轴承所产生的力为:

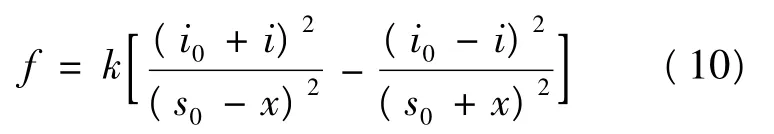
式中:k=μ0Aln2/4，μ0为真空中的磁导率，Al为磁极的截面积，n为线圈的匝数;i0为平衡位置的偏置电流;s0为转子在平衡位置时的气隙大小;i为控制电流;x为转子偏离平衡位置的位移，其方向垂直向上。

由牛顿定律得转子的运动方程为:

式中:m为转子的质量;¨x为转子的加速度;p为转子受到的扰动力。

2.2 系统辨识仿真

为使支持向量机解决控制问题，笔者采用典型的辨识结构如图3所示。图3中，u为被控对象输入，即输入电流;y为被控对象的实际输出，即转子位移;e为辨识器输出与实际输出之间的偏差，即辨识误差，它取决于SVM的近似能力。

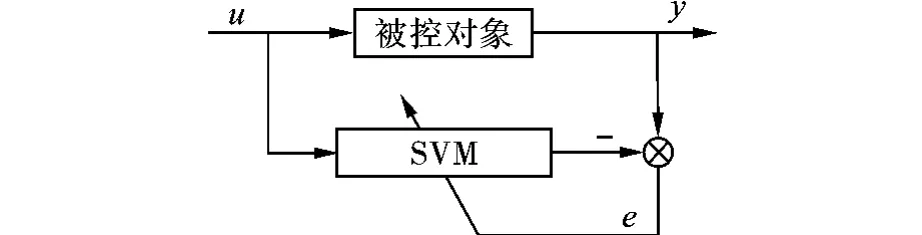
图3 基于SVM的辨识结构

磁力轴承具有负刚度和零阻尼，在开环状态下不能稳定工作，输入输出数据必须在闭环状态下采集。PID控制器的控制性能虽不理想，但能够使转子在平衡位置附近一定范围内稳定悬浮，因此可以在PID控制器的控制下采集样本数据集。采用的PID参数为:kp=2.5，ki=312.5，kd=0.015。通过式(10)和式(11)产生输出位移y(t)。为保证被辨识系统持续充分激励，且所建模型具有较好的泛化能力，闭环系统运行一段时间后，在磁力轴承转子位移不发散的前提下在PID控制器的输出端加入一个随机扰动量r。这里，选择均方差为0.01的高斯白噪声作为随机扰动量。

闭环磁力轴承系统框图如图4所示。加入幅值为410的阶跃输入(该幅值对应于推力盘离开平衡位置0.1 mm的数字量)。根据对象的输入输出数据集，用SVM来对其动态行为建模。通过实验产生200组样本点(ui，yi)。图5为对象输入电流u(t)采样集。

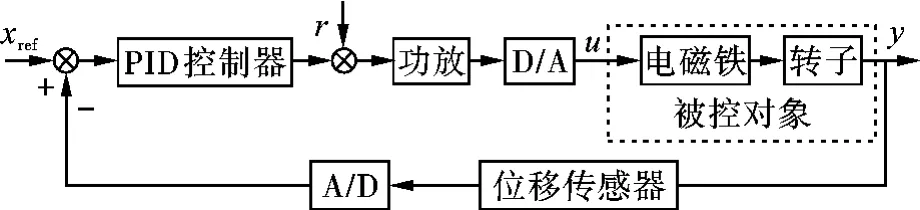
图4 闭环磁力轴承系统

图5 对象输入电流采样集

因磁力轴承系统是二阶系统，故可采用拟合因子:x(k)=[y(k)，y(k－1)，u(k)，u(k－1)]T，可得200个训练样本[x(k)，y(k+1)]，将训练样本集分成两部分，选80个样本用来训练，剩下的120个样本用来测试训练后的SVM性能。笔者采用基于Matlab平台下的Libsvm仿真。

仿真实验中核函数根据先验经验采用径向基核函数，通过网格寻优法[12]选择最优的惩罚参数和核参数，C=32，σ =0.03，训练误差 ε=0.001。图6为SVM输出测试集的拟合，最小均方根误差只有0.007。由图6可见，训练过的SVM能够产生与测试值基本相同的输出，其拟合的误差范围在 10－5级上。

为对比辨识效果，利用BP神经网络对相同的训练样本和测试样本进行系统辨识和预测，取4－20－1的结构，隐含层为Tansig函数，输出层为线性函数，训练函数选trainbfg，仿真的结果如图7所示。从图7中可以看出，SVM的拟合效果比BP算法的拟合效果好，误差相差小。BP算法可能存在过拟合。

再增加10倍的采样频率，再次采样对200组数据集进行拟合，发现SVM的拟合精确度更高。如图8所示。跟随误差数量级在10－7以上。因此，可用该SVM辨识模型作为磁力轴承模型进行控制器的设计或者以其为基础调整磁力轴承PID控制器的参数。

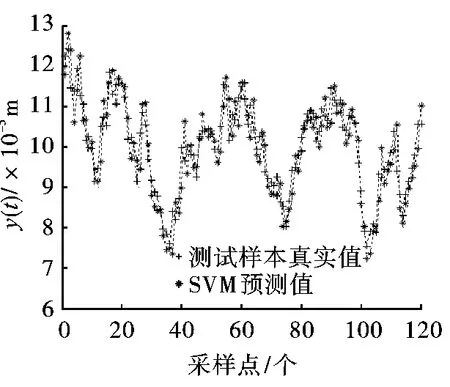
图6 SVM输出测试集拟合

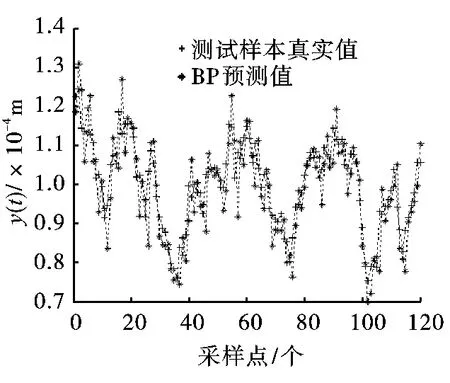
图7 BP输出测试集拟合

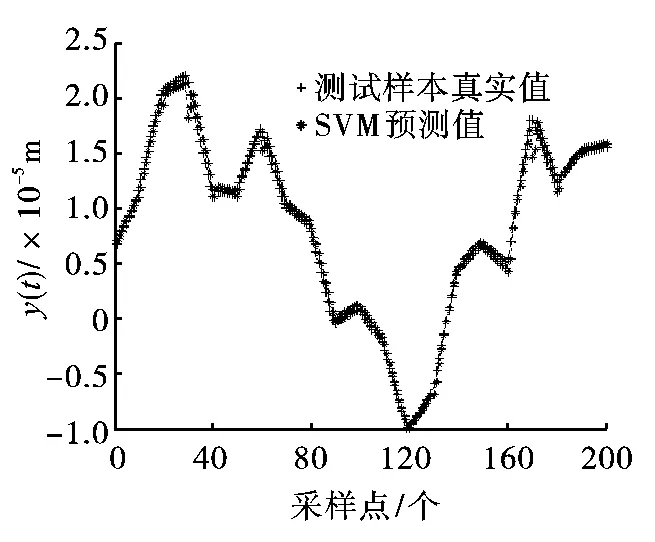
图8 高频时SVM输出测试集拟合

3 结论

支持向量机是一种新的机器学习方法。它较好地解决了传统学习方法中的小样本、非线性、高维数、局部极小点等实际问题，具有很强的泛化能力。将支持向量机应用于磁力轴承系统的辨识，并进行仿真实验研究，仿真结果显示该SVM模型能较好地拟合输出位移，证明了该辨识方案的可行性和有效性。

[1] G·施韦策，H·布鲁勒，A·特拉克斯勒.主动磁轴承基础、性能及应用[M].北京:新时代出版社，1997:27－45.

[2] 张丹红，陈建华，苏义鑫，等.主动磁力轴承系统的模糊逆建模[J].中国电机工程学报，2006，26(14):126－130.

[3] 戴云，杨静，张华容.自校正PID调节器在单自由度磁浮轴承中的应用[J].自动化技术与应用，2001(6):1－2.

[4] 杨作兴.单纯形法实现系统辨识及其在磁轴承中的应用[J].数值计算与计算机应用，2000(3):226－232.

[5] 林盾，陈俐.BP神经网络在模拟非线性系统输出的应用[J].武汉理工大学学报:交通科学与工程版，2003，27(5):731 －734.

[6] 苏义鑫，龙祥，周祖德，等.主动磁轴承的神经网络辨识研究[J].武汉理工大学学报:交通科学与工程版，2005，29(5):689 －692.

[7] 朱国强，刘士荣，俞金寿.支持向量机及其在函数逼近中的应用[J].华东理工大学学报，2002，28(5):555－559.

[8] JOBERG J，ZHANG Q H，LJUNG L，et al.Nonlinear black－box modeling in system identification:a unified overview[J].Automatica，1995，31(12):1691 －1724.

[9] 张浩然，韩正之，李昌刚.基于支持向量机的未知非线性系统辨识与控制[J].上海交通大学学报，2003，37(6):927 －930.

[10] VAPNIK V.Statistical learning theory[M].New York:John Wiley，1998:437 －468.

[11] 邓乃扬，田英杰.支持向量机理论、算法与拓展[M].北京:科学出版社，2009:18－21.

[12] 闫国华，朱永生.支持向量机回归的参数选择方法[J].计算机工程，2009，35(13):218 －220.