风电锁紧盘轴套位移与应力计算

陶德峰，王建梅，黄讯杰，康建峰，侯 成

(太原科技大学机械工程学院，太原030024)

风电锁紧盘是风力发电机增速器的专用件。它包括外套1、内环2、螺栓3和垫片4，其中外套内孔与内环外圆均为圆锥面。风电锁紧盘在装配时，内环受外套作用被压紧并传递压力，同时内环作用轴套使其产生变形，从而在轴套与主轴接触面产生结合压力，使轴套5与主轴6紧密地联结为一体，具体结构如图1所示。

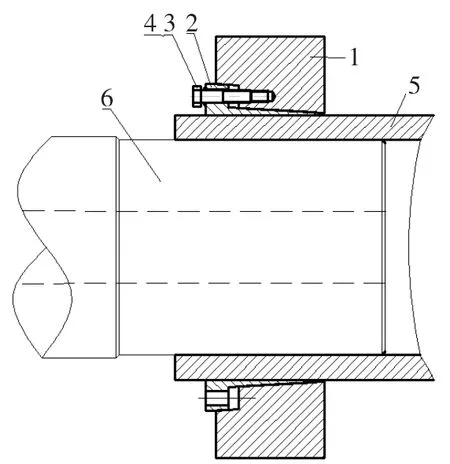
图1 结构示意图Fig.1 The scheme of structure

风电锁紧盘装配完成后，各接触面过盈量(2 mm以下)相对于各部件的尺寸较小;同时要求风电锁紧盘拆装15次各部件不发生塑性变形，所以对轴套内表面位移和最大应力计算的精确性要求较高。但是将轴套由实际工况简化为平面问题，采用厚壁圆筒理论计算其内表面位移和最大应力所得结果的误差大小并不明确[1-3]。因此，有必要对其进行理论解析和数值模拟计算，对比两种方法计算结果及其相对误差，分析各因素对轴套内表面位移和最大应力的影响，以保证计算结果的精确性。

1 计算分析

1.1 模型参数

以风电锁紧盘的某型号轴套作为分析对象建立三组轴套模型，分别考虑外压、内半径、外半径对轴套内表面位移、最大应力及其理论值与模拟值相对误差的影响。各组模型参数如表1所示。

表1 各组模型参数Tab.1 The parameters of each group

1.2 理论解析计算

将轴套简化为平面问题的厚壁圆筒，如图2所示。圆筒内半径和外半径分别为a、b，材料弹性模量为E，泊松比为μ，所受内压和外压分别为p1、p2.

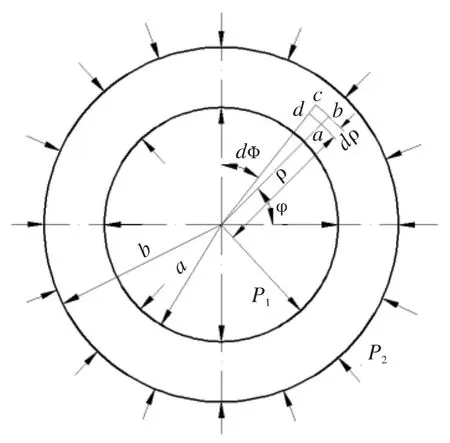
图2 厚壁圆筒模型示意图Fig.2 The scheme model of thick-cylinder

1.2.1 位移计算

由变形几何关系、静力平衡方程、物理方程可得筒壁内任一点的径向位移公式[4]:

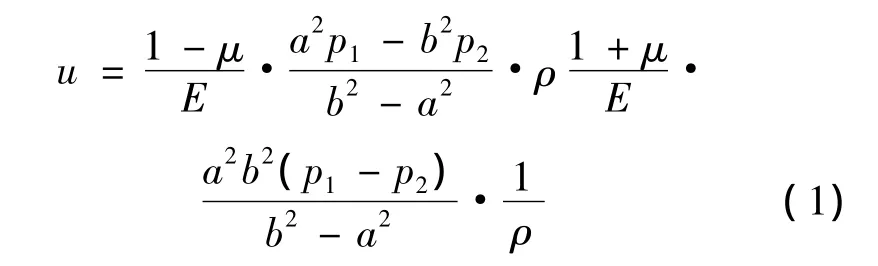
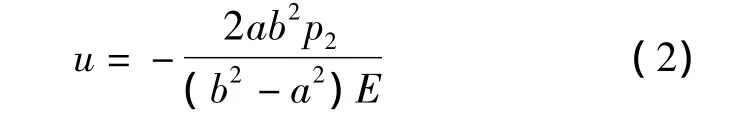
1.2.2 最大应力计算

由变形几何关系、静力平衡方程、物理方程可得筒壁内任一点应力表达式[4-6]:

式中，ρ为筒壁内任一点至轴套中心线的距离，a≤ρ≤b.

将p1=0，ρ=a代入式(1)，整理即得轴套只承受外压时内表面径向位移计算公式:

应力σi为:

对于上式，当ρ=a时，σi取得极大值，

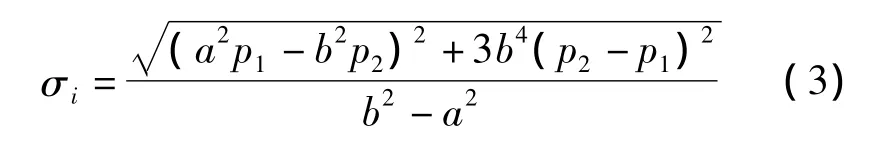
1.3 有限元数值模拟

采用有限元分析软件ANSYS对模型进行计算。根据风电锁紧盘的实际工况，将模型一端轴向约束，另一端无约束;模型采用 solid 186单元[7-8]，弹性模量E为180 GPa，泊松比 μ为0.3，密度为7 800 kg/m3;模型网格轴向划分为20份，周向为120份。在圆筒外表面施加内法向方向载荷以模拟所承受外压。由于风电锁紧盘装配过程时间长、速度慢，冲击对变形影响很小，所以采用静态分析[9]，模型如图3所示。

将p1=0代入式(3)，整理即得轴套只承受外压时最大应力计算公式:

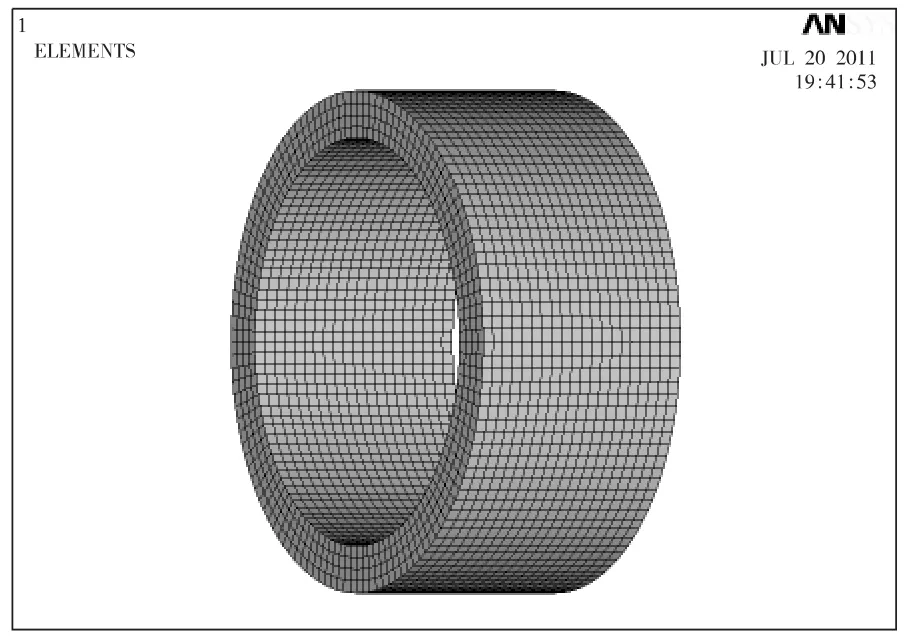
图3 有限元模型Fig.3 FEM model

2 计算结果与分析

2.1 位移云图与应力云图

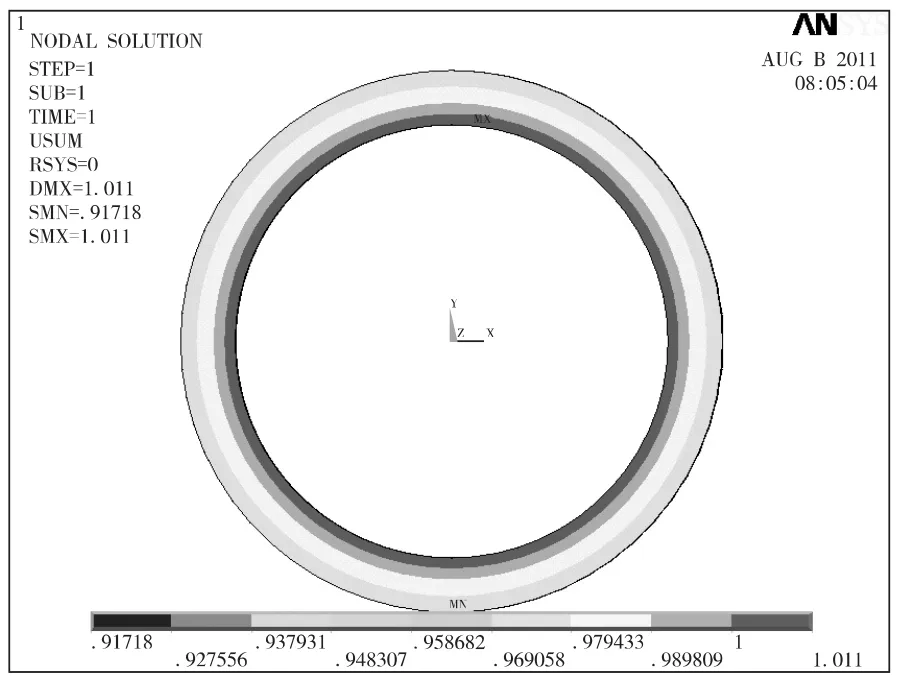
图4 位移云图Fig.4 Displacement vector sum

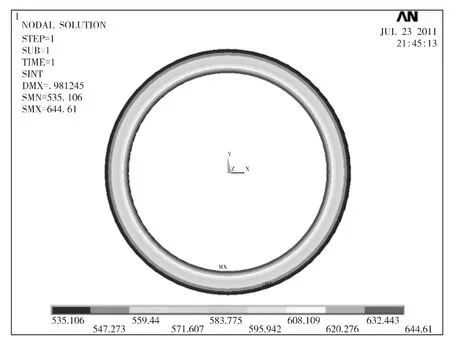
图5 应力云图Fig.5 Stress intensity

图4和图5分别为轴套模型的位移云图、应力云图。

由图4和图5可知，轴套在只承受外压时，最大位移和最大应力均发生在轴套内表面。

2.2 轴套内表面位移与最大应力

表2为第1组模型即内半径为a=260 mm，外半径为b=320 mm，不同外压p2时，轴套内表面位移和最大应力计算结果。

表2 第1组模型计算结果Tab.2 The calculation results of the first group

表3为第2组模型即外半径为b=320 mm，外压为p2=120 MPa，不同内半径a时，轴套内表面位移和最大应力计算结果。

表3 第2组模型计算结果Tab.3 The calculation results of the second group

表4为第3组模型即内半径为a=260 mm，外压为p2=120 MPa，不同外半径b时，轴套内表面位移和最大应力计算结果。

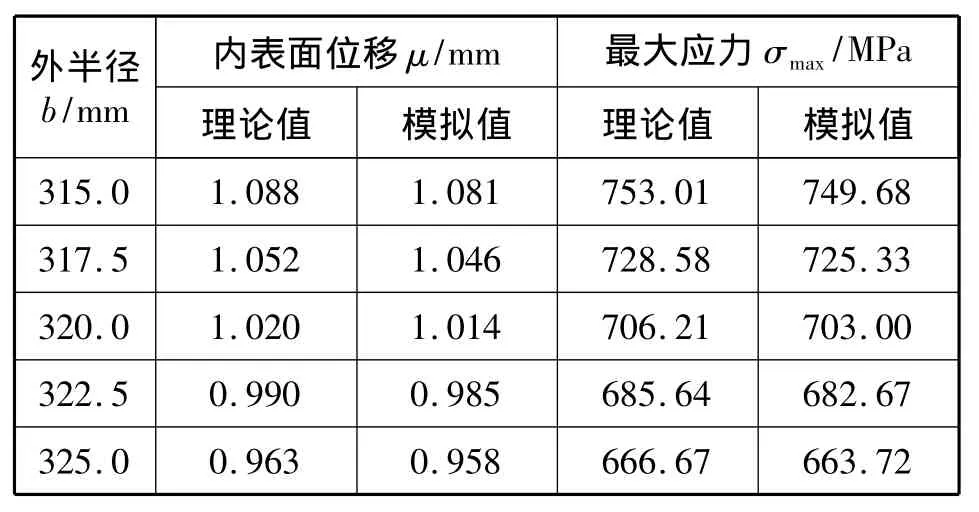
表4 第3组模型计算结果Tab.4 The calculation results of the third group

由表2、表3可知，随着外压、内半径的增大，内表面位移和最大应力随之增大，即内表面位移和最大应力与外压、内半径成正比。由表4可知，随着外半径增大，内表面位移和最大应力随之减小，即内表面位移与最大应力与外半径成反比。

2.3 轴套内表面位移和最大应力的理论值与模拟值相对误差

记相对误差S:

根据式(5)计算三组模型内表面位移和最大应力理论值与模拟值的相对误差。

图6为第1组模型即内半径为a=260 mm，外半径为b=320 mm，不同外压p2时，轴套内表面位移和最大应力的理论值与模拟值相对误差计算结果。

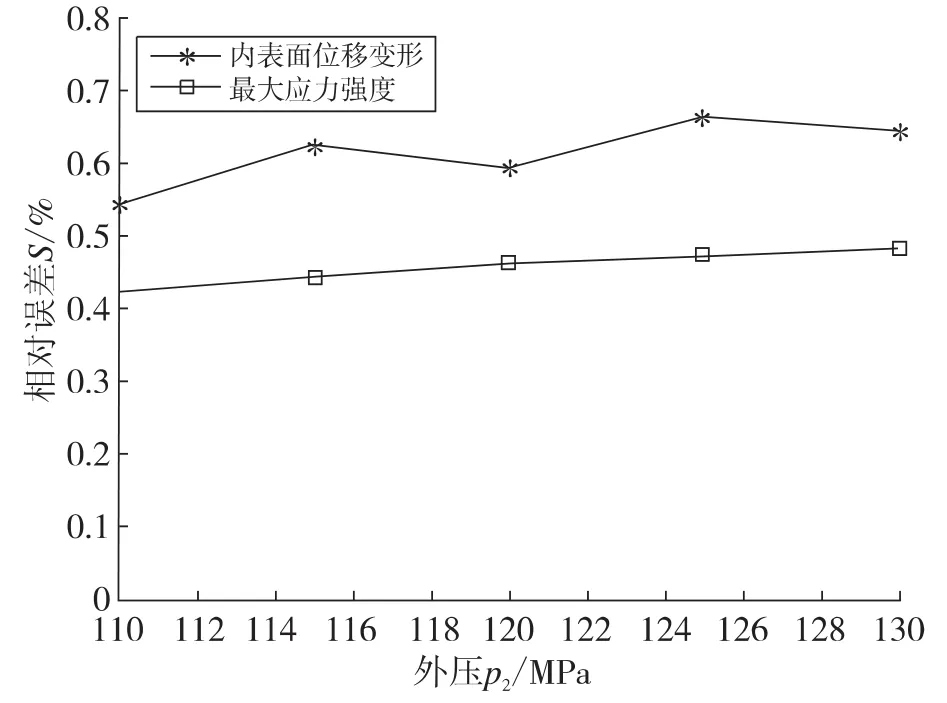
图6 第1组模型内表面位移和最大应力的理论值与模拟值相对误差Fig.6 The relative error between theoretical results and simulating results of the first group’inner surface displacement and greatest stress intensity

图7为第2组模型即外半径为b=320 mm，外压为p2=120 MPa，不同内半径a时，轴套内表面位移和最大应力的理论值与模拟值相对误差计算结果。

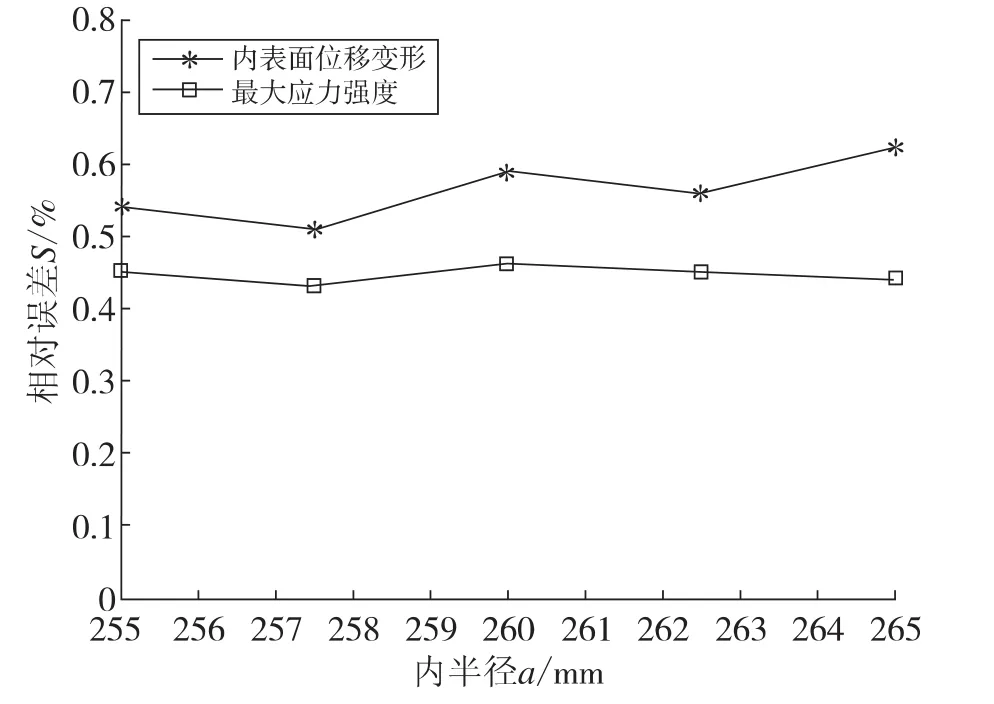
图7 第2组模型内表面位移和最大应力的理论值与模拟值相对误差Fig.7 The relative error between theoretical results and simulating results of the second group’inner surface displacement and greatest stress intensity

图8为第3组模型即内半径为a=260 mm，外压为p2=120 MPa，不同外半径b时，轴套内表面位移和最大应力的理论值与模拟值相对误差计算结果。

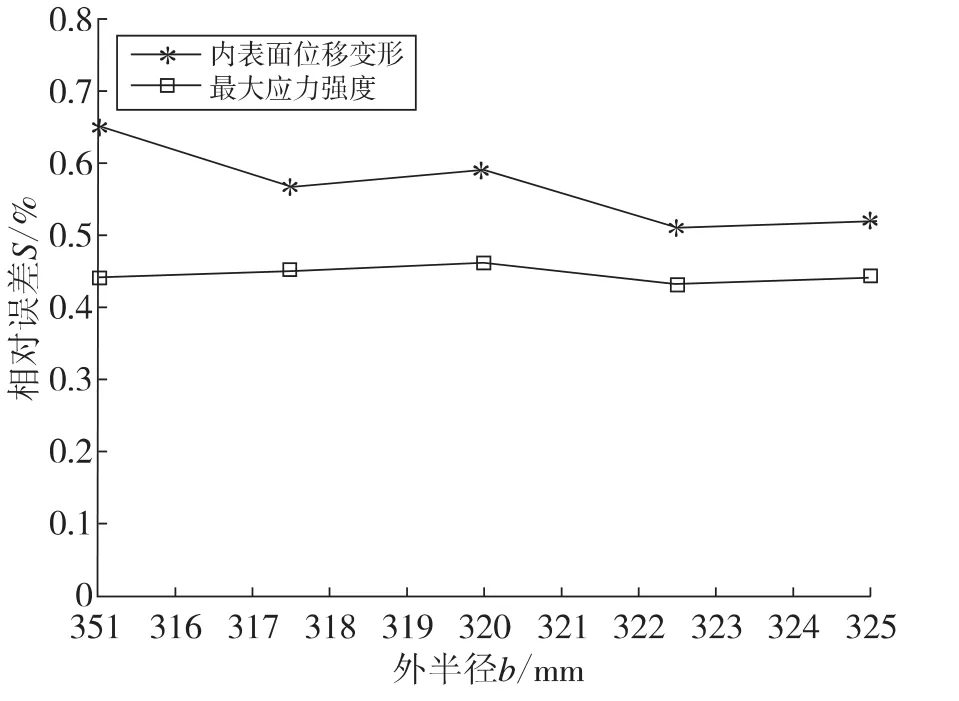
图8 第3组模型内表面位移和最大应力的理论值与模拟值相对误差Fig.8 The relative error between theoretical results and simulating results of the third group’inner surface displacement and greatest stress intensity

由图6-图8可知，三组模型的内表面位移和最大应力计算结果的理论值与模拟值相对误差处于1%以内，表明理论计算结果和有限元计算结果几乎相等。同时由图可知，内表面位移的理论值与模拟值相对误差大于最大应力的理论值与模拟值相对误差。

3 结论

(1)轴套在只承受外压时，最大位移和最大应力均发生在轴套内表面。

(2)轴套的内表面位移和最大应力与其外压、内半径成正比，与其外半径成反比。

(3)轴套内表面位移和最大应力的理论值与模拟值比较吻合，其相对误差均在1%之内;同时，内表面位移的理论值与模拟值相对误差大于最大应力的理论值与模拟值相对误差。

(4)根据两种计算结果知将轴套由实际工况简化为无轴向力的平面应变问题，采用厚壁圆筒理论计算其承受外压时内表面位移和最大应力所得结果是比较准确的，能够满足风电锁紧盘设计需求。

[1]邹雨，庄茁，黄克智.超弹性材料过盈配合的轴对称平面应力解答[J].工程力学，2004(6):72-75;83.

[2]岳普煜，王建梅，马立峰，等.热连轧机油膜轴承弹性过盈装配研究[J].太原科技大学学报，2006，27(4):301-305.

[3]廖焰，刘建生，陈慧琴.新型空心火车车轴重要结构参数有限元分析[J].太原科技大学学报，2006，27(6):446-450.

[4]刘鸿文.材料力学[M].4版.北京:高等教育出版社，2004.

[5]吴家龙.弹性力学[M].北京:高等教育出版社，2001.

[6]王连仲.锁紧盘联接的设计计算及其应用[J].化工粉体工程设计，1998(2):33-36.

[7]王新荣，陈永波.有限元法基础及ANSYS应用[M].北京:科学出版社，2008.

[8]张朝晖，李树奎.ANSYS11.0有限元分析理论与工程应用[M].北京:电子工业出版社，2008.

[9]石亦平，周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社，2006.