一秩元集上完全保反对合性的可加映射

刘 敏，黄 丽，李俊林

(太原科技大学应用科学学院，太原030024)

近几十年来，许多学者对算子代数或算子空间上保持某种性质、子集、函数或关系等不变量的映射的刻画问题进行了研究，其结果表明，许多情形下这样的映射是代数同态或代数反同态的，从而揭示了算子代数或算子空间的代数或几何结构性质[1-3].Hadwin和Larson[4]2003年引入了完全秩不增的线性映射的概念;文献[5]和文献[6]分别刻画了无限维实或复Banach空间上的标准算子代数上完全保持幂等元，平方零元和斜幂等元的满射问题，证明了这样的映射是同构或(复情形下)共轭同构的;文献[7]给出了反对合矩阵的若干性质。在此基础上，考虑一秩元集上完全保反对合性的可加映射的刻画问题。

1 定义

令X，Y表示实数域或复数域F上的无限维Banach空间，X*表示X的对偶空间，R表示一秩元集，用I1(X)表示R上的所有一秩幂等元的集合。称T为反对合算子，若T2=-I，对任意的x∈X，f∈X*，x⊗f表示由y→(y，f)x定义的一秩算子。一秩算子x⊗f是幂等的当且仅当f(x)=1.P⊥Q表示P和Q正交，P⊥Q⇔PQ=QP=0.设映射 Φ∶R→ℵ，对于每个n∈ℕ ，定义映射为 Φn∶R⊗Mn(F)→ℵ⊗Mn(F)为 Φn((sij)n×n)=(Φ(sij))n×n，则如果Φn保反对合性，称Φ是n-保反对合性的;如果对于每个正整数n，Φ是n-保反对性的，则称Φ是完全保反对合性的。

2 主要结果和证明

为了证明主要定理，需要引入引理1.

引理1[5]设X，Y是实数域或复数域F上的无限维Banach空间，P⊆B(X)，Q⊆B(Y)是任意包含所有秩一幂等元的幂等元集。令Φ∶P→Q是一个双射，如果Φ双边保正交性，则要么存在一个有界可逆线性或(复情形下)共轭线性算子A∶X→Y，使得Φ(T)=ATA-1，T∈P，要么存在一个有界可逆线性或(复情形下)共轭线性算子A∶X*→Y，使得Φ(T)=AT*A-1，T∈P.在第二种情形中，X和Y一定自反。

定理1 令X，Y是实数域或复数域F上的无限维Banach空间，R，ℵ分别是X和Y上的一秩元的集合。设Φ∶R→ℵ是一个可加满射，则下列陈述等价:

(i)Φ是双边完全保反对合性的映射;

(ii)Φ是双边2-保反对合性的映射;

(iii)存在有界可逆线性或(复情形下)共轭线性算子A∶X→Y使得:Φ(T)=cATA-1

对每个T∈R成立，其中c=±1.

证明 显然有(iii)⇒(i)⇒(ii)，下面只需证明(ii)⇒(iii).

假设Φ是双边2-保反对合性的映射。

断言1 Φ(0)=0，Φ(I)=±I，且Φ是单射。

因为Φ是可加映射，对于任意的T∈R，由于:

是R⊗M2⊆B(X2)中的反对合元，所以有:

也是一个反对合元，因此有:

在矩阵(1)中取T=0，有

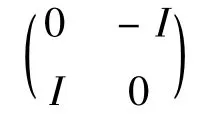
是R⊗M2⊆B(X2)中的反对合元，所以

也是一个反对合元，所以有:

再在矩阵(1)中取T=I，有

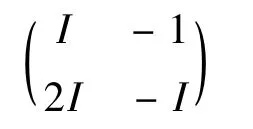
是R⊗M2⊆B(X2)中的反对合元，所以

也是一个反对合元，所以有:

因为Φ是一个满射，由方程(2)可得Φ(I)与ℵ中的每个元可交换，又由方程(5)可得:Φ(I)=cI，c=±1.由方程(3)和方程(5)可得Φ(0)2=0，在方程(2)中取T=0之后加方程(4)可得Φ(I)Φ(0)=0，所以 Φ(0)=0.

下面证明Φ是单射。

对任意的T，S∈R，满足Φ(T)=Φ(S)，则有:

对于 Φ(I)=-I，可以令 Ψ(T)=-Φ(T)，则有 Ψ(I)=-Φ(I)=-(-I)=I.对于A，B，C，D∈R，假设是反对合算子，则，所以Φ双边保反对合性时，Ψ也是双边保反对合性的映射，所以后面一直假设Φ(I)=I.

断言2 存在有界可逆线性或共轭线性算子A∶X→Y，使得Φ(T)=ATA-1，对于任意的T∈I1(X)都成立。

首先证明Φ双边保一秩幂等元的正交性。

所以Φ双边保一秩幂等元。

所以Φ是I1(X)上双边保一秩幂等元的正交性的双射。在引理1中取P=Q=I1(X)，则有:

(a)存在一个有界可逆线性或(复情形下)共轭线性算子A∶X→Y，使得:Φ(T)=ATA-1，T∈I1(X);

(b)存在一个有界可逆线性或(复情形下)共轭线性算子A∶X*→Y，使得:Φ(T)=AT*A-1，T∈I1(X).

在第二种情形中，X和Y一定自反。

现在证明第二种情况不可能出现。

假设Φ(T)=AT*A-1.对于所有的T∈I1(X)成立。对于任意的x∈X，一定存在非零的f1，f2∈X*，使得＜x，f1＞=1，＜x，f2＞=0，令f=f1-f2，g=f1+f2，从而有x⊗f，x⊗g∈I1(X)，所以

是R⊗M2⊆B(X2)中的反对合元，而:

因此Φ(T)=ATA-1对每个T∈I1(X)都成立，断言2成立。

令 Ψ ∶R→ℵ为Ψ(T)=A-1Φ(T)A，则Ψ是一个双射，Ψ(I)=I，且Ψ(T)=T，∀T∈I1(X).下面要验证 Ψ2保反对合性。取Ti∈ R(i=1，2，3，4)，使得)是反对合元，则:

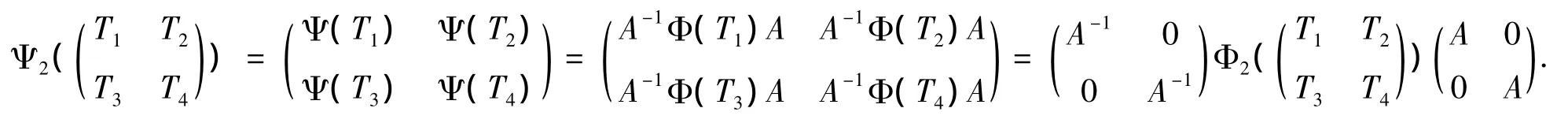
由于Φ2双边保反对合性，所以Ψ2也是双边保反对合性。不失一般性，下面假设Φ(T)=T，其中T∈I1(X).

断言3 对于任意的秩一元x⊗f，Φ(x⊗f)=λx⊗f(x⊗f)成立，其中0≠λx⊗f∈F.

对于任意的一秩元x⊗f，其中x∈X，f∈X*，对于任意的h∈X*，取y∈X，使得＜y，h＞=1.则:

h∈x⊥且是反对合元⇔

即h∈x⊥⇔h∈{ran Φ(x⊗f)}⊥且y∈kerf⇔f∈ker(Φ(x⊗f)).

所以Φ(x⊗f)=λx⊗f(x⊗f)对于某个 λx⊗f∈F{0}成立。

断言4 对于任意的x⊗f∈R{0}有λx⊗f=1，从而Φ(x⊗f)=x⊗f成立。

对任意的一秩非零元x⊗f，其中x∈X，f∈X*，是反对合元，所以也是反对合元，此蕴涵所以即Φ2(x⊗f)=Φ((x⊗f)2)，所以(λx⊗fx⊗，即，所以 λx⊗f=1.

这样就完成了(ii)⇒(iii)，证毕。

[1]侯晋川，崔建莲.算子代数上线性映射引论[M].北京:科学出版社，2002.

[2]路召飞，黄丽，李俊林.保持算子乘积谱函数并零的映射[J].太原科技大学学报，2011，32(1):59-62.

[3]HOU J C，CUI J L.Additive maps On standard operator algebras preserving invertibilities or zero divisors[J].Lin Alg Appl，2003，359:219-233.

[4]HADWIN D，LARSON D R.Completely rank-nonincreasing linear maps[J].J Funct Anal，2003，199:210-227.

[5]HOU J C，HUANG L.Maps completely preserving idempotents and maps completely preserving square-zero operators[J].Israel Journal Of Mathematics，2010，176:363-380.

[6]黄丽，路召飞，李俊林.标准算子代数上完全保斜幂等性的可加映射[J].中北大学学报，2011，32(1):71-73.

[7]邹本强.对合矩阵和反对合矩阵的若干性质[J].金华职业技术学院学报，2007，7(2):88-90.