带回溯线搜索的新锥模型信赖域算法

郎立勤，王希云

(太原科技大学应用科学学院，太原030024)

基于无约束优化问题:

信赖域算法无疑是一种非常成功的算法，其中f:Rn→R为二阶连续可微函数，目前有众多学者对其进行了深入的研究。传统的信赖域算法主要是利用二次模型来逼近目标函数，即构造二次模型对问题(1)进行求解，然而对于非二次性态强、曲率变化较为剧烈的函数，逼近的效果往往不是很好。针对这一缺陷，1980年Davidon[1]提出了锥模型，使模型更加一般化，之后倪勤[2]等提出了新的锥模型信赖域子问题，取消了对信赖域半径和水平向量的限制，克服锥函数的可能无界性，为进一步研究锥模型方法开拓了一片广阔的发展空间。

新锥模型信赖域子问题:

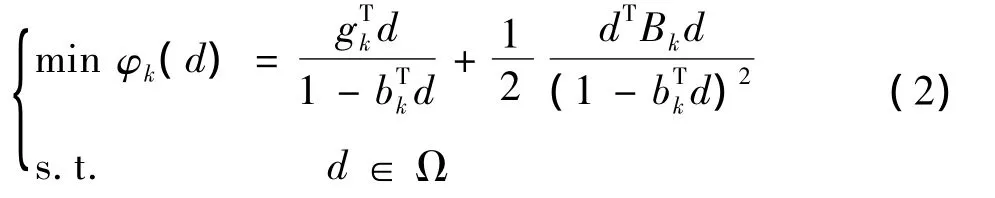
其中Bk是f(x)在xk点的海森阵或海森阵近似，gk=-▽f(xk)，并且

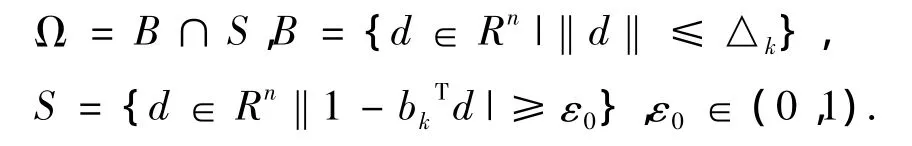
求解信赖域子问题时，当试探步dk不能作为成功的迭代点时，也就是说当新求得的dk会使得目标函数值上升的时候，总可以沿着dk方向进行回溯的线搜索，以致找到使目标函数下降的点。这里说的回溯线搜索实际上就是充分利用当前迭代点的信息构造一个αk，找到一个满足:

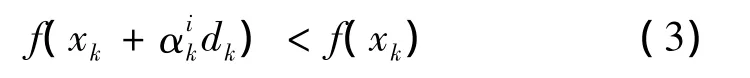
的最小的整数i.其中 αk∈(0，1)，并且 αi+1kdk∈[a1，a2]αi

kdk，0 ＜a1＜a2＜1.唐明筠[3]利用高阶的插值得到的如下形式的αk:

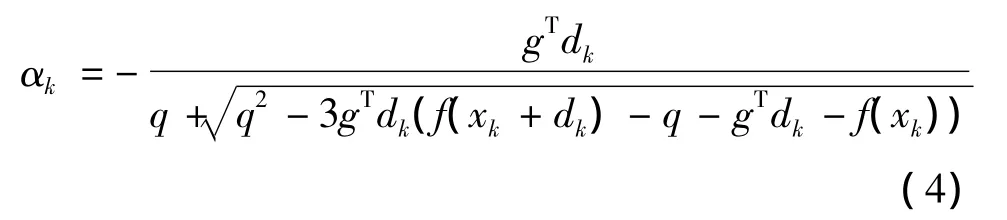
由于当迭代失败时重解子问题付出的代价会很高，这里将回溯线搜索应用到新锥模型信赖域方法上构造了一类新的带线搜索的算法，减少了计算量，提高了计算效率。其中自适应信赖域半径的调节是参考文献[4]中的确定，c∈(0，1)，p是非负整数。

1 算法

实际下降量和预测下降量的比值:

下面给出带回溯线搜索的自适应新锥模型信赖域算法的具体步骤:

步0 给定x0∈Rn，对称矩阵B0∈Rm×n，△0＞0，τ ＞0，0≤μ1≤μ≤1，β∈(0，1)，α∈(0，1)，0 ＜c＜1，ε ＞0，p=0，k:=0，M=0.

步1 计算‖gk‖，若‖gk‖≤ε，则停止;否则转步2.

步2 用折线法求解该子问题的近似解dk.

步 3 计算 ρk，若 ρk≥μ，则令xk+1=xk+dk;否则利用式(4)计算αk，进行回溯线搜索寻求满足的最小的正整数i，令xk+1=

步4 若 ρk≥ μ，令

若 ρk≤μ1，令‖gk+1‖;否则，令△k+1= △k.

注:本文中Bk，bk的更新采用锥模型拟牛顿法，同文献[5]。

2 算法的收敛性

I={k:ρk≥μ}，J={0，1，…}I

H1:水平集L(x0)={x|f(x)≤f(x0)}是有界的，而且xk∈L(x0);

H2:数列{fk}有下界;

H3:存在正的常数σ，使得‖Bk‖≤σ，‖bk‖≤σ，∀k;

引理1[3]算法产生的点列{xk}满足:

总体而言，目前对于马克思哲学终极关怀内容的研究正在蓬勃兴起，但尚未形成较为成熟的体系与规模。马克思哲学终极关怀思想作为其超越维度的核心核心内容之一，彰显了马克思以人为终极目的的真切关注和对人意义世界的开创性探索，因此对于这一问题的厘清和解决势必将会对马克思哲学超越维度的整体性呈现奠定重要的理论基础。

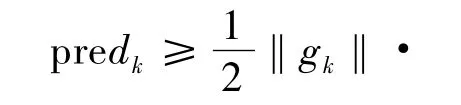
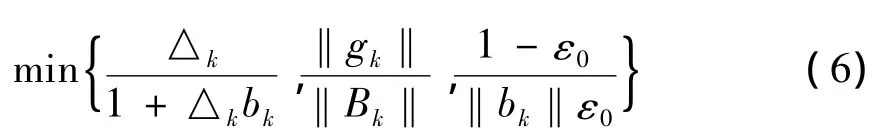
引理2[6]若H2成立，则数列{fl(k)}非增并且收敛。

引理3[7]若H1-H3成立，且由本文算法产生的点列为{xk}满足‖gk‖≠0，那么存在，当≥△k时就有△k+1≥△k.

基于上述的引理，可以得到以下的全局收敛性结论。

定理1 如果H1-H3均成立，那么由算法产生的点列{xk}会满足

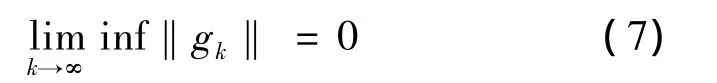
证明 (用反证法)假设之上结论是不成立的，则必然存在常数ε＞0和正常数K，使‖gk‖≥ε，∀k≥K.由引理1和本文的算法可以知道，对于任意的成功的迭代步dk总有

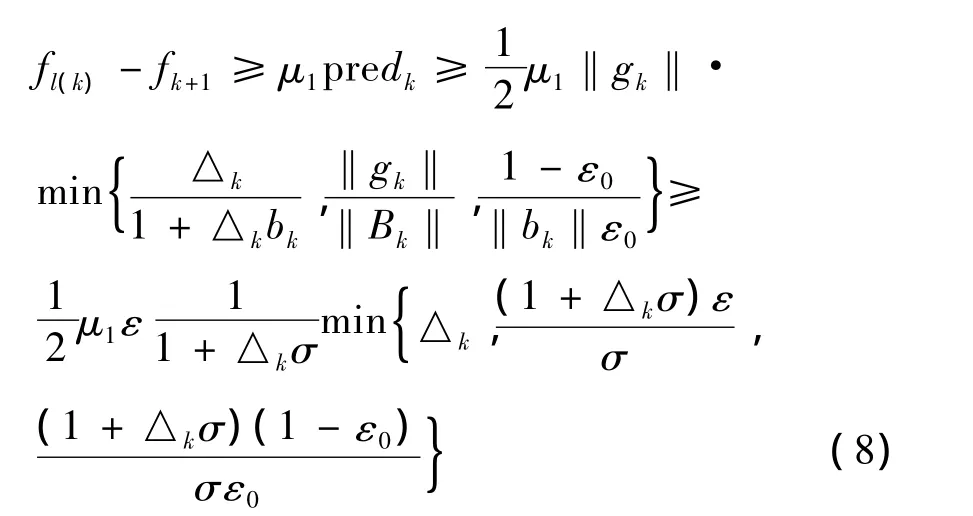
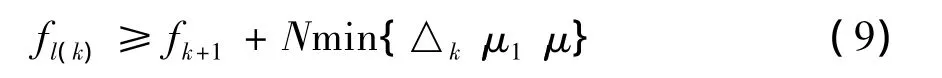
以此类推下去，有:

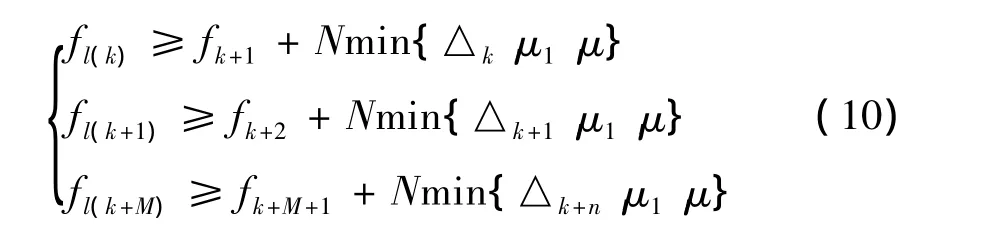
根据{fl(k)}的定义容易得到:

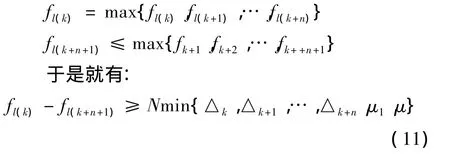
由引理2可知{fl(k)}收敛，所以可得:.这与引理3矛盾，即结论得证。证毕。

定理2 若H1-H3均成立，而且由本文算法产生的点列{xk}满足‖g*‖=0，▽2f(x)在x*附近连续并且▽2f(x*)正定，如果，则可以得到{xk}Q-二阶收敛于x*.

证 明 用 反 证 法 证 明。令 κ=，下面证明κ中只有有限个元素。

这里假设κ中有无穷个元素，那么结合假设条件可以知道:

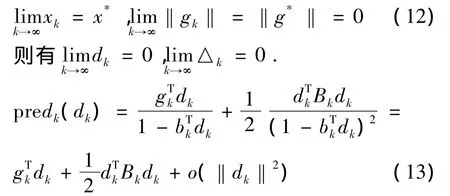
当k充分大时，就有

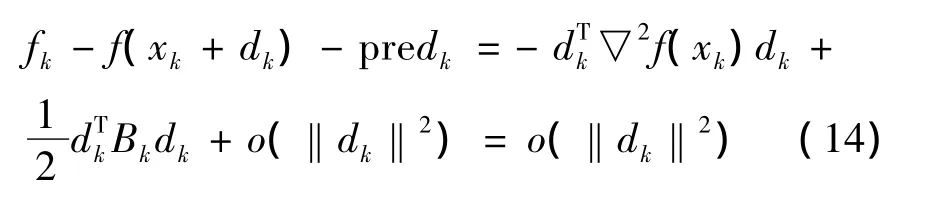
于是，

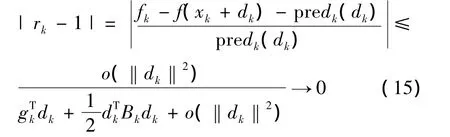
即有rk→1.由本文的算法可以知道，对于充分大的k有rk＞μ成立，于是就有△k+1≥△k，这与产生矛盾，所以κ中只有有限个元素。因此对充分大的k有，于是，dk=，此时算法采用的是牛顿下降步，所以{xk}Q-二阶收敛于x*.证毕。

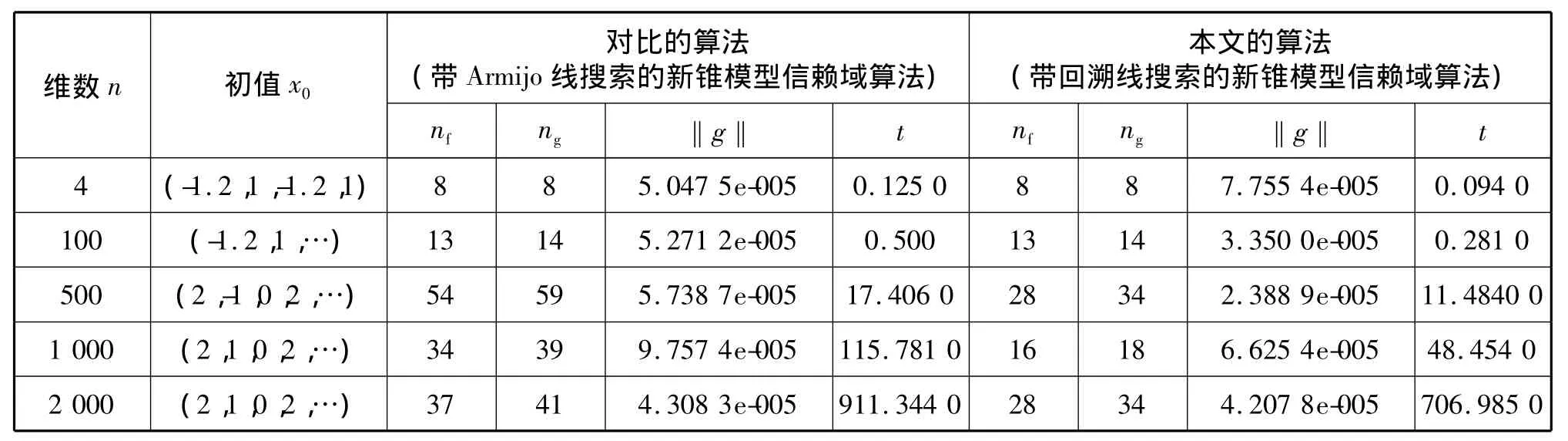
表1 数值测试结果Tab.1 Numerical results

3 数值实验

从数值结果可以看出:无论从迭代次数上还是计算结果上都可以看出带回溯线搜索的自适应信赖域算法比带Armijo线搜索的锥模型信赖域算法计算效率要高，而且从运算需要的时间上可以看出，本文的算法确实更加经济省时，在数值试验上基于新锥模型的算法也是可行的，稳定的。但是在解决一些大规模问题上还有待深入研究。

[1]DAVIDON D C.Conic approximations and collinear scaling for optimizers[J].SIAM J Numer Anal，1980，17(2):268-281.

[2]吴海平，倪勤.一个新锥模型信赖域算法[J].高等学校计算机数学学报，2008，30(1):57-67.

[3]唐明筠.带回溯线搜索步的双子问题信赖域算法[J].工程数学学报，2010，27(4):626-636.

[4]ZHANG X S，ZHANG J L，LIAO L Z.An adaptive trust region method and its convergence[J].Science in China:series A，2002，45:619-631.

[5]赵绚，王希云.一类新的带线搜索的自适应非单调信赖域算法[J].太原科技大学学报，2010，32(1):67-71.

[6]李红，焦宝聪.一类带线搜索的自适应信赖域算法[J].运筹学学报，2008，12(2):97-104.

[7]王希云，王庆.一种新锥模型非单调信赖域算法[C]//中国运筹会第九届交流会论文集.北京:中国运筹学会，2008:110-116.