基于三阶拟牛顿方程的对角三阶拟牛顿法

冯茹茹，王希云

(太原科技大学应用科学学院，太原030024)

无约束优化问题的一般形式为:

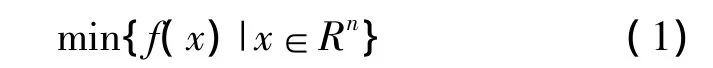
其中f:Rn→R为二次连续可微函数，fk表示f(xk)，gk表示▽f(xk)。定义dk=-Hkgk为拟牛顿方向，其中Hk为Hessen矩阵的逆近似，要求Hk正定且满足拟牛顿条件

其中yk-1=gk-gk-1，sk-1=xk-xk-1.在拟牛顿算法中，存储量至少为O(n2)。如果用稀疏矩阵来逼近Hessen阵的逆，要求存储量为O(n)，且近似满足拟牛顿条件。对角稀疏拟牛顿算法的提出使存储量和工作量明显减少，适合于大规模稀疏问题的求解。

1988 年，Barzilai和 Borwein[1]提出两点步长法，迭代公式为xk+1=xk-Dkgk，其中Dk=αkI是一个矩阵。为了使Dk具有拟 Newton性质，计算 αk使min‖sk-1-Dkyk-1‖，得

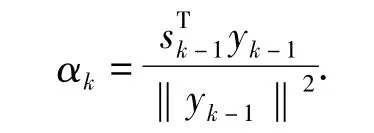
时贞军[2]提出了对角稀疏拟牛顿法，该算法在每次迭代中利用对角矩阵近似拟牛顿法中的校正矩阵，通过求解得到min‖Hkyk-1-sk-1‖2得到Hk，从而构造对角稀疏拟牛顿法。

之后，很多学者对此类算法进行了研究，其中对角二阶拟牛顿法[3]对Hessen阵具有二阶逼近阶;孙清滢，崔彬[4]和郑艳梅[5]分别将 Grippo 非单调线搜索和Zhang H.C.提出的非单调线搜索引入对角稀疏拟牛顿法进行了研究。

基于三阶拟牛顿方程[6]

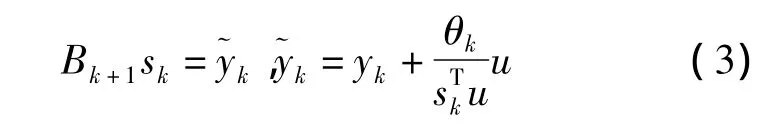
来获得Hessen阵的正定对角矩阵逆近似，同时将Zhang H.C.[7]提出的非单调线搜索规则与时贞军提出的大步长线搜索技巧结合设计求解无约束优化问题的对角三阶拟牛顿法。

1 对角三阶拟牛顿法

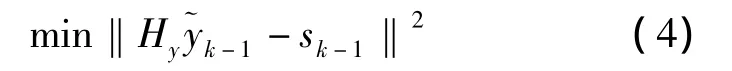
为保证搜索方向dk=-Hkgk为下降方向，要求，因此有问题(SP)

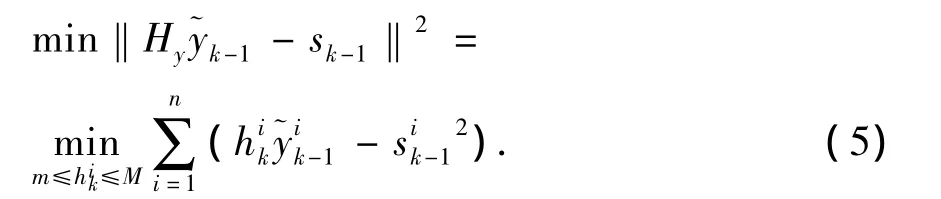
在问题(SP)中，m，M取正常数。

算法1(DSQN):

(Ⅰ)∀x0∈Rn，H0=In，C0=f0=f(x0)，Q0=0＜ηmin≤ ηmax＜1，k=0，ε＞0.

(Ⅱ)若‖gk‖ ＜ε，则停，否则转(Ⅲ)。

(Ⅲ)令dk=-Hkgk，其中Hk由式(5)确定，转(Ⅳ)。

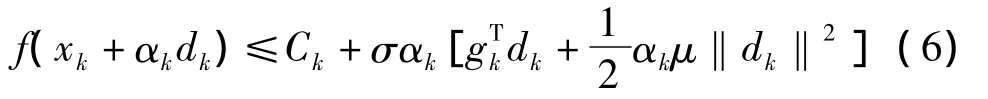
令xk+1=xk+αkdk，fk+1=f(xk+1).

(Ⅴ)通过某种规则给出 ηk∈[ηmin，ηmax]，

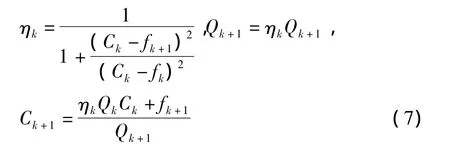
令k∶=k+1，转(Ⅱ)。

引理1 若xk不是问题(SP)的稳定点，则有‖dk‖≤M‖gk‖.

引理2 若xk不是问题(SP)的稳定点，则有

引理 3[7]对∀k有，fk≤Ck.

2 全局收敛性

假设1f(x)在水平集L(x0)={x∈Rn|f(x)≤f(x0)}上有下界。

假设2f(x)的梯度g(x)在水平集上Lipschitz连续，即存在常数L＞0，使得‖g(x)-g(y)‖≤L‖x-y‖，∀x，y∈L(x0).

证明 令K1={k|αk=sk}，K2={k|αk＜sk}(i)如果k∈K1，则由式(6)及引理1和2，可以得到:

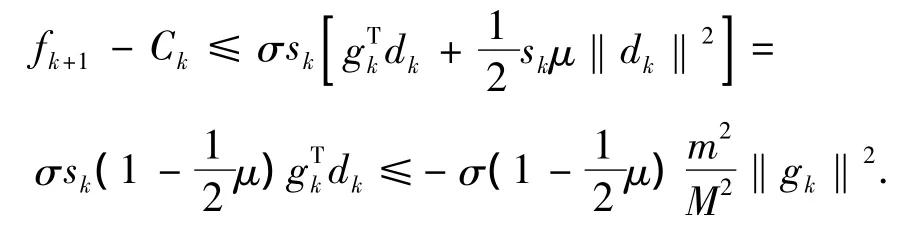
(ii)如果k∈K2，则 αk＜sk，由线搜索规则及引理3知，对∀k∈K2有:

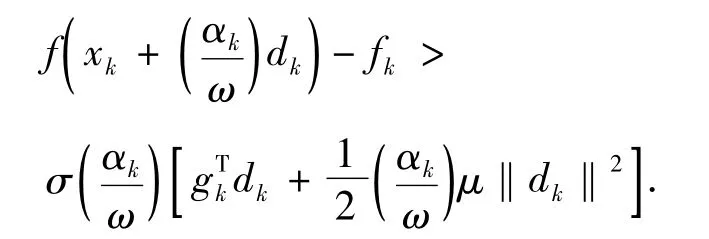
再由中值定理及 αk∈{sk，ωsk，ω2sk，…}，存在θk∈[0，1]和正整数i≥1 使得

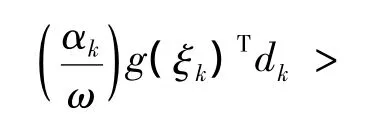
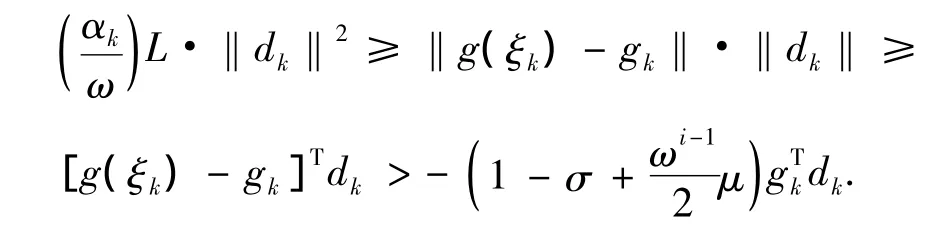
由假设2，Cauchy-Schwartz不等式，式(8)得:

由上式可得:

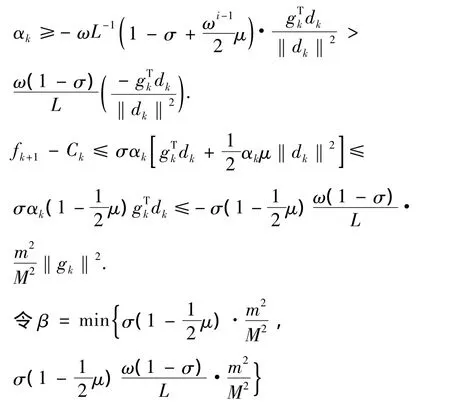
则由(i)和(ii)可得

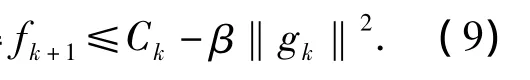
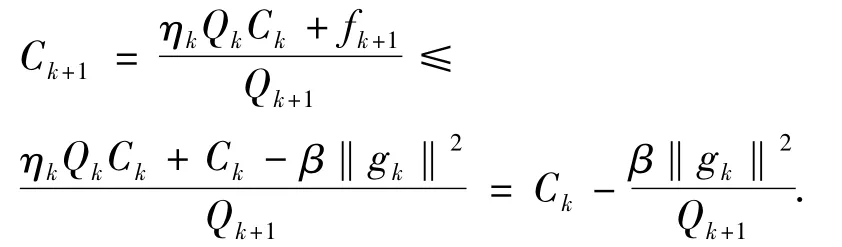
因为f(x)有下界，且对∀k有，fk≤Ck，所以Ck有下界。由上式可得:

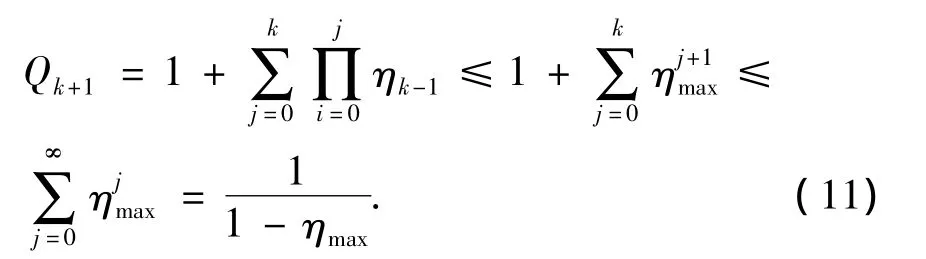
由ηmax＜1及式(7)知:由式(10)和式(11)可得.证毕。

3 超线性收敛性

假设3f(x)在极小点x*的邻域内二次连续可微，且存在ε＞0，M'＞m'＞0使得当

‖x-x*‖＜ε，∀y∈Rn，有

m'‖y‖2≤yT▽2f(x)y≤M'‖y‖2;

假设4 ▽2f(x)在极小点x*的某邻域内Lipschitz连续，即且存在ε＞0，

‖▽2f(y)-▽2f(x)‖≤γ‖x-y‖，∀x，y∈N(x*，ε).

其中r是Lipschitz常数。

定理2 假设1、2、3均成立，若算法产生无穷点列{xk}收敛到局部极小点x*，即xk→x*，但xk≠x*，若

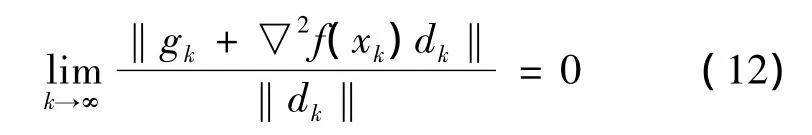
则:(1)当k充分大时，αk=1;(2)序列{xk}超线性收敛到x*.

证明 (1)由引理1及定理1可知‖dk‖→0.利用泰勒展开及引理1、2有

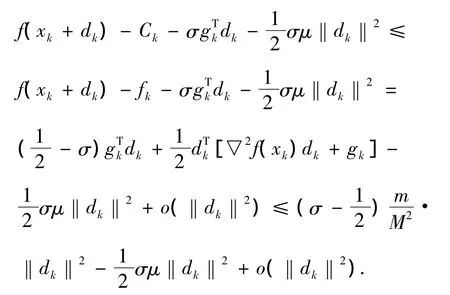
当k充分大时‖dk‖2]，即当k充分大时，σk=1满足算法算法1中的线搜索规则。

(2)可仿照文献[1]证明{xk}超线性收敛到x*的充要条件为式(12)。

4 数值结果

利用MATLAB程序，将算法1与文献[1]中的对角稀疏拟牛顿法进行了比较，详细结果见表1.

用IT表示算法的迭代次数，T表示所用时间，fopt表示目标函数的最优值。下面分别给出维数N=100，2 000，5 000，10 000 的计算结果。当N＜2 000，在精度满足fk-f*≤10-8时，可以得到问题的精确解。当N≥2 000，在精度满足fk-f*≤10-6时算法迭代停止。

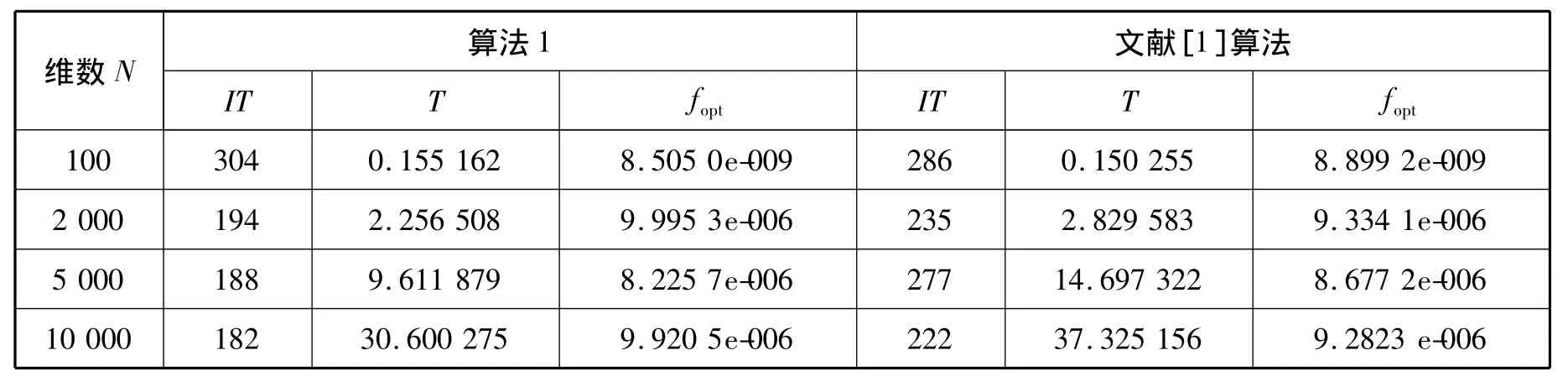
表1 算法1与对角稀疏拟牛顿法的数值结果Tab.1 The numerical results from the method 1 and diagonal sparse quasi-Newton method

计算结果表明，当维数增加时，迭代次数的增加最不敏感，反而有一定的减少。从整体上看，基于三阶拟牛顿方程的对角三阶拟牛顿法比对角稀疏拟牛顿法计算效率要高，适合求解大规模无约束优化问题。

[1]BARZILAI J，BONWEIN J M.Two-point step size gradient methods[J].IMA Journal Of Numerical Analysis，1988，8:141-148.

[2]时贞军，孙国.无约束优化问题的对角稀疏拟牛顿算法[J].系统科学与数学，2006，26(1):101-112.

[3]潘义勇，潘平奇.无约束优化问题的对角二阶拟牛顿算法[C]//中国运筹学会第九届学术交流会论文集.北京:中国运筹学会，2008:64-68.

[4]孙清滢，崔彬，王长钰.新非单调线搜索规则的 Lampariello修正对角稀疏拟牛顿算法[J].计算数学，2008，30(3):255-269.

[5]孙清滢，郑艳梅.大步长非单调线搜索规则的Lampariello修正对角稀疏拟牛顿算法的全局收敛性[J].数学进展，2008，37(3):311-320.

[6]ZHANG J Z，XU C X.Properties and numerical performance of quasi-Newton methods with modified quasi-Newton equations[J].J Comput Appl Math，2001，137:269-278.

[7]ZHANG H C，WILIAM W HAGER.A nonmonotone line search technique and its application to unconstrained optimization[J].J SIAM J Optim，2004，14(4):1043-1056.

[8]朱帅，王希云.一类Armijo搜索下的记忆梯度法及其全局收敛性[J].太原科技大学学报，2010，31(3):249-251.