基于幂级数多项式的基带预失真技术分析

陈宝文，韩 军

(中国电子科技集团公司第五十四研究所，河北石家庄050081)

0 引言

随着通信技术的飞速发展，多电平(M-QAM)多载波调制技术(WCDMA，OFDM等)得到了广泛应用，而这些技术无一例外地都属于非恒包络调制技术，因此对功率放大器的非线性非常敏感。功放的非线性会引起带外频谱扩张，产生邻信道干扰，带内失真则引起误码的上升，严重影响通信系统的性能。因此功放的线性化技术就变得尤为重要。

功率放大器的线性化技术有很多种［1，2］，相比于其他线性化技术，自适应数字基带预失真法由于引入了自适应算法，并且在基带进行处理，不涉及复杂的射频信号处理并可以实时跟踪功放的变化特性，因此可以很好地校正功放的非线性。

而数字基带预失真法又可以分为基于多项式的预失真法和基于查询表技术的预失真法［3］。由于查询表预失真技术的效果直接受到表项大小的影响，且当功放非线性较严重时就需要大量表项，甚至多维表项，此时表的自适应收敛就会非常慢，预失真性能严重下降，因此使用基于幂级数多项式的预失真法。

1 基本原理

数字基带预失真技术的基本原理就是基带信号首先经过预失真器的预处理，而预失真器的传输特性则刚好是功放传输特性的反函数，这样最后经过放大器后输出信号就只有线性的增益了［4］。其基本原理如图1所示。

图1 数字预失真技术的基本原理图

图2给出了预失真技术的实现原理:当输入信号为rin时，由于非线性特性，功放的实际输出小于所期望的线性输出α·rin，但同时可以看到当功放输入为rin-pd时，则输出为α·rin。因此可以在功放前端加一预失真器，如果输入为rin，则预失真器输出为rin-pd，再经过功放后就使系统输入输出呈现线性关系了。

图2 数字预失真技术实现原理图

2 系统结构

基于幂级数多项式的数字基带预失真技术结构如图3所示。

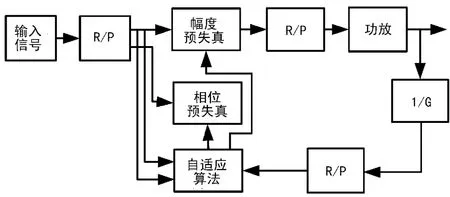
图3 基于幂级数多项式的基带预失真系统结构

如图3所示，输入信号经过直角坐标/极坐标(R/P)的转换，而后经过幅度、相位预失真器后，再经过R/P转换进入功率放大器(仿真中假设ADC/上变频、DAC/下变频均为理想情况，因此可忽略)，反馈回路耦合一部分信号(1/G，G为功放期望线性放大倍数)后与源信号比较产生误差，从而自适应地调整幅度、相位预失真器，当两者达到收敛后，功放实现线性输出。

2.1 幂级数多项式预失真器

假设功率放大器的失真只受幅度和相位的影响，设输入的信号为:

则放大器的输出可以表示为:

式中，r(t)ejθ(t)是输入信号的复包络，wc为载波频率，G(·)、Φ(·)代表功放的幅度和相位传输函数。预失真的目的就是提供一个正好与功放非线性特性相反的预失真器，使得最后达到线性输出的效果。假设源输入信号为vo(t)=ro(t)ejθo(t)，则预失真器相应的输出为:

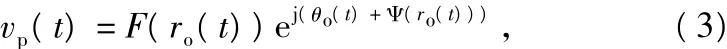
函数F(·)和Ψ(·)表示预失真的多项式。理想情况下有:

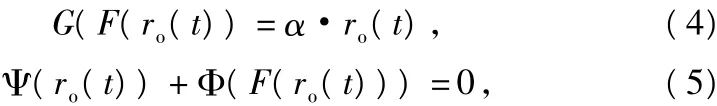
式中，α·ro(t)为期望的功放线性输出，将将F(·)和Ψ(·)2个非线性的方程用多项式表示为:

以上2式即是幅度和相位预失真器的预失真函数。

2.2 预失真系数更新自适应算法-LMS算法

LMS算法是一种常见的自适应算法，以其结构简单、复杂度低、易于实现为被广泛采用。要求得式(6)、式(7)中的最佳预失真向量V和P，就是要使得下面定义的2个均方误差最小:

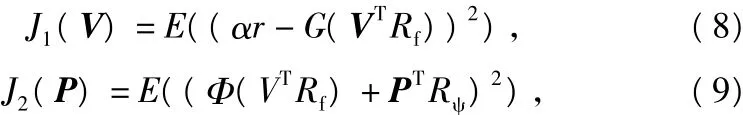
按照LMS迭代算法，向量V的迭代公式为:

式中，μk为迭代步长因子，根据功放特性G’(VkTRf，k)近似为 1，则上式可以写成:

相位预失真是得到一个与Φ(F(ro(t))相反的相位偏移，使其与放大器产生的相位偏移正好抵消。

同理有:

2.3 功放模型

功放模型在预失真系统中占有重要地位，选择文献中经典的Saleh模型［5］，该模型很好地描述了窄带功放的AM-AM、AM-PM特性，其表达式如下:

其中:α1=2.158 7，β1=3.151 7，α2=4.003 3，β2=9.104 0。

2.4 衡量预失真性能关键指标

衡量预失真系统预失真性能的主要指标为邻信道功率比(ACPR)和误差矢量幅度(EVM)［6，7］。

ACPR定义为:邻信道功率与主信道功率的比值，用来衡量对邻信道干扰的大小。ACPR越低，那就意味着功放的三阶及五阶交调越低，功放的线性度越好。

EVM定义为:误差矢量信号平均功率的均方根值和参考信号平均功率的均方根的比值，并以百分数形式表示。EVM越小，说明功放的非线性对信号的影响就越小。

3 仿真结果分析

仿真中采用16 QAM信号，该信号经过滚降因子为0.25的平方根升余弦滤波器后进入预失真器。

从图4可以看出，经幂级数多项式预失真后，ACPR较传统的极坐标查询表预失真改善了10 dB左右，达到了－50 dB(仿真中，查询表预失真技术在表项N=64时ACPR为－40 dB，且继续增加表项时，ACPR不再改善)。

图4 预失真前后功率谱密度的比较

图5是信号经查询表预失真(a)及幂级数预失真(b)后星座图的情况，从中可以看出，经幂级数预失真后，星座图得到了明显改善，EVM从6.43%降低为1.67%，基本消除了功放非线性所引起的星座图扩散和旋转效应。

图5 预失真前后星座图的比较

图6是功放的AM-AM(幅度－幅度失真)曲线比较图，图中左侧为经查询表预失真后的AM-AM曲线，右侧为经幂级数预失真后的AM-AM曲线，可以看出，幂级数预失真方法较传统的查询表预失真效果更优，功放输入输出基本呈现线性关系。

图6 预失真前后AM-AM曲线

4 结束语

主要介绍了一种基于幂级数多项式的数字基带预失真技术，该技术通过将输入信号分别进行幅度预失真和相位预失真，较好地纠正了功放的非线性。仿真表明，ACPR较查询表预失真技术改善了10 dB左右，EVM由6.43%降低为1.67%，星座图得到了很好地纠正，AM-AM曲线基本呈现了线性关系，达到了线性化目的。

［1］沈小虎，金浩，王德苗.射频功率放大器数字预失真技术及其发展趋势［J］.电信科学，2010(8):59－65.

［2］李铭祥.微波功放的线性化技术［J］.微波学报，2002，18(1):83－87.

［3］艾渤，杨知行，潘长勇等.基于LUT的HPA数字基带预失真方法研究［J］.电子与信息学报，2007(7):1580－1583.

［4］马进.数字预失真基本原理［J］.电子科技，2006，9:17－21.

［5］王勇，向新，易克初.基于多项式的记忆型数字基带失真器［J］.西安电子科技大学学报，2006，33(2):223－226.

［6］CHENH H，LIN C H.Joint Polynomial and Look-up-Table Predistortion Power Amplifier Linearization［J］.IEEE Transactions on Circuits and Systems-II:Express Briefs，2006，53(8):612 －616.

［7］范秀利，郑建宏，陈莉.TD-SCDMA的EVM测试及分析［J］.重庆邮电学院学报，2005，2:156 －159.