一种构造系数的自相关函数特征提取算法

张立民，刘 峰，，张瑞峰

(1.海军航空工程学院，山东烟台264001;2.中国人民解放军92785部队，河北秦皇岛066200)

0 引言

遥感影像分类作为遥感影像处理过程中的重要步骤，已经远远超出了人的分析和解译能力，为了达到理想的分类效果，提取深层次空间结构信息的需求越来越强烈，受到广大科研人员的重视。由于遥感影像具有数据量大、维数高和不确定性等特点，应用支持向量机对其进行分类是目前主要发展的一个方向［1，2］，可以解决传统空间特征提取模型处理高维数据存在的难以收敛、计算复杂和结果难以解释等问题［3－5］。对于基于支持向量机的遥感影像分类问题，一般情况下，都是直接使用样本自身数据进行分类，没有提取样本特征，忽略了样本数据中隐含的空间信息，Randen T等人在提取纹理结构信息时验证这些隐含的空间信息对于分类来说是有帮助的［6］，因此本文提出一种新的自相关函数特征提取方法，将其应用于遥感影像空间特征提取，最后基于支持向量机方法，将提取的自相关函数特征与样本数据组合成新的样本，对新的样本数据进行训练与分类性能研究。

1 支持向量机与自相关函数

1.1 支持向量机

支持向量机是统计学习理论结构风险最小化SRM原则的实现方法［7］。它是从线性可分情况下的最优分类面发展而来的，基本思想可用图1来说明。图中，实心点和空心点代表2类样本，H为分类线，H1和H2分别为过各类中离分类线最近的样本且平行于分类线的直线，它们之间的距离叫做分类间隔(margin)。所谓最优分类线就是要求分类线不但能使2类正确分开(训练错误率为0，而且使分类间隔最大。对分类线方程(w·x)+b=0进行标准化处理，使得对线性可分的样本集:

满足 yi((w·x)+b)≥1，i=1，…，l，此时分类间隔等于2/‖w‖，使间隔最大等价于使‖w‖/2最小，训练样本正确可分，且使‖w‖/2最小的分类面就是最优分类面，位于H1和H2的训练样本点称作支持向量。

图1 2类线性分类的最优分类面

在实际应用中，大多数情况下都是非线性问题，因此需要引入惩罚系数C，来控制特殊样本的分类，另外需要通过非线性变换将输入变量x转化到某个高维空间中，然后在变换空间求最优分类面。应用标准的Lagrange乘子法解算，根据KKT定理，构建最优分类面的问题可转化为下面的对偶二次规划问题:

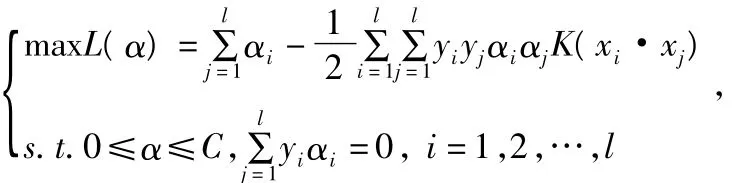
最终的分类函数为:

由于上面的对偶问题只涉及训练样本之间的内积运算，即在高维空间只需要进行内积运算，根据泛函的有关理论，只要1种核函数K(xi，xj)，满足Mercer条件［8］，它就对应某一变换空间中的内积，可以用K(xi，xj)间接地计算特征空间中输入向量的像之间的内积，从而可以避免维数灾难问题。

1.2 自相关函数特征提取算法

在随机过程理论中，样本的自相关函数，在一定程度上能够反映样本的空间结构信息。通常1个样本都是由多个特征值组成的，将样本特征值映射为1个数值序列:

式中，li为样本第i个特征的值;N为样本的特征数。数值序列的自相关函数定义为:

由上式可以看出，根据m取值的不同，会产生m个自相关函数值。

大多数情况下，训练样本并不充分，或者某一类样本过少，导致基于这些样本的分类精度较低，对样本的自相关函数特征进行加权可以改善分类效果，通过样本的均值、方差和样本数构造1种新的加权系数。设第c类样本数为Mc，样本用S表示，则第c类样本的均值和方差为:

由于均值和方差能够反映样本的分布特性，按照样本不充分情况下加权系数应与均值方差之积成反比的原则，构造第c类样本加权系数Wc为:

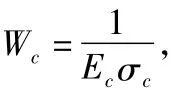
然后对自相关函数值加权，将样本特征值与这m个自相关函数值相结合，组成样本新的特征向量，可表示为:

式中，m取值必须小于N，因此就需要讨论m取多少时得到的分类精度最优，本文将针对遥感影像数据对m取值不同情况下的分类精度进行讨论。

2 数据库与特征提取

2.1 数据库

实验数据库采用UCI机器学习数据库的遥感影像数据库，此数据库的每个样本由4个波段3*3图像区域的遥感数据组成，样本的类别由位于区域中心的像素确定，样本的类别用数字表示。此数据库共有4 435个训练样本和2 000个测试样本，每个样本具有36个特征属性，分别为这9个像素在4个波段的遥感数据，支持向量机采用林智仁教授开发的LIBSVM软件包对样本数据进行训练与分类。表1为数据库各类别样本个数。

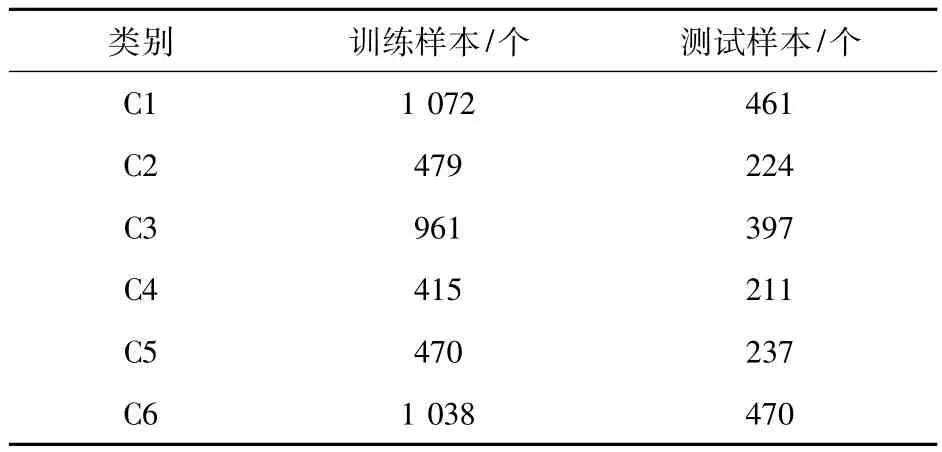
表1 数据库各类别样本个数

2.2 遥感影像自相关函数特征提取

由于每个样本是1个4波段3*3区域的遥感数据，因此每个样本每个波段共9个遥感数据，可以将样本每个波段的遥感数据按照从左至右、由上至下的顺序排成1个共9个元素的序列，每个样本共4个这样的序列，假设这4个序列分别为{Si，i=1，2，3，4}，每个序列中的元素为{lj，j=1，2，…，9}，根据上述构造加权系数算法提取特征值，由表1可以看出，每类样本添加自相关函数特征后样本的特征为:

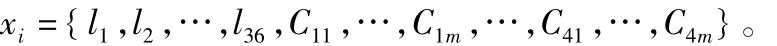
3 实验和讨论

为了验证本文自相关函数特征对遥感影像分类的有效性和可行性，本次实验分2步进行，第1步用支持向量机对未添加自相关函数特征的训练样本进行学习，然后对测试样本进行分类，记录分类精度;第2步用支持向量机对添加自相关函数特征的训练样本进行学习，并分别对m取值不同情况下(即添加的自相关函数特征数目不同)的样本进行训练，然后分别对测试样本进行分类，并记录m取值不同情况下的分类精度，与第1步实验结果进行比较与讨论。

3.1 基于支持向量机的遥感影像分类实验

本次实验选用径向基核函数，由于此数据库说明文档中注明不要使用交叉验证方法来获取最优C值、最优g值和最优分类精度，可能会因为内存不足等原因而导致失败，训练样本和测试样本只能用来分类和预测，因此在选择惩罚系数C时，只选用了3个特殊的值，g取默认值1。首先对训练样本和测试样本进行归一化处理，然后用支持向量机进行训练和分类，分类结果如表2所示。

表2 惩罚系数C取值不同时的分类精度

为了讨论m取值不同情况下对分类性能的影响，必须将C值和g值固定，为方便起见，本次实验选用C取值为10，g取默认值1。这样，根据表2可知此时总分类精度为83%，在此情况下，样本各类别分类精度Q如表3所示。

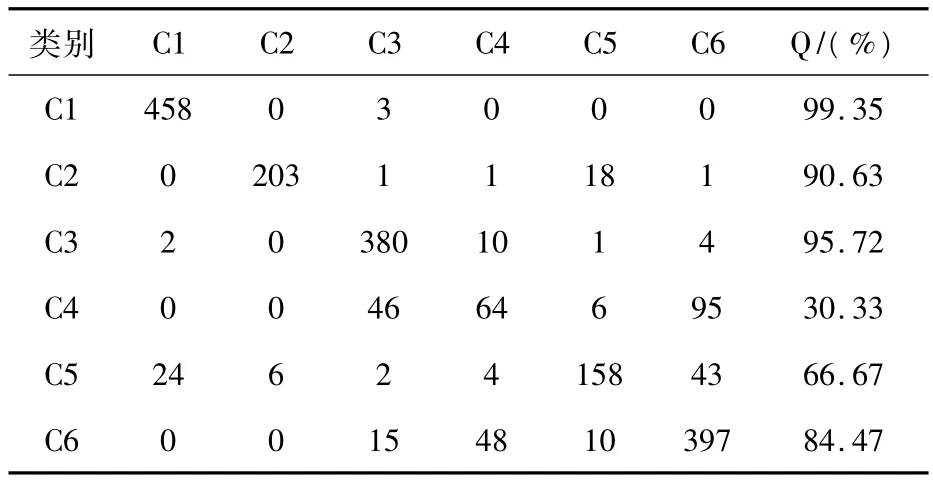
表3 数据库各类别样本个数

3.2 基于支持向量机的遥感影像分类实验

根据上述讨论，支持向量机选用径向基核函数，选定了参数C值和g值，在此基础上，根据自相关函数特征提取方法，分别对m从1到8取值进行计算，将其特征值添加到样本数据中形成新的样本数据，然后用支持向量机对其进行训练与分类，仅取其中m值为偶数列于表中，其分类结果如表4所示。

表4 基于支持向量机的遥感影像分类结果

从表3和表4可以看出:① 添加构造加权系数自相关函数特征后，样本的总分类精度得到了不同程度的提高，在m取值为4时，样本的分类精度提高了大约3个百分点，说明此算法能够改善样本的分类精度，对于遥感影像分类是有效和可行的;②在支持向量机初始参数选定的情况下，m取值不同总分类精度也不同，在一定程度上影响了分类结果，在对具体问题进行分类时需要具体分析，例如有些样本空间结构较粗，在样本区域的选择上需要探讨和优化;③样本中类别4的分类精度较其他类别的分类精度低很多，我们认为是由于它和类别6在数据上非常相似，两者难以区分，造成分类误差较大，这个问题有待进一步研究;④ 当m＞4时，样本的总分类精度基本保持在85.50%附近，类别1和6的分类精度几乎没变，其他各类的分类精度有1%左右的变化，我们认为这与各类样本的支持向量有关，因为支持向量的个数与学习机器的复杂性有关，随着样本特征数目的变化而导致学习机器分类精度的变化。

4 结束语

本文从自相关函数特征提取算法的角度出发，提出了一种构造加权系数的算法。分别对原始样本和添加了构造加权系数自相关函数特征的样本进行训练与分类，实验结果表明此算法能够提高样本的分类精度，验证了此算法的有效性与可行性，但此算法仅涉及样本的均值和方差，还有许多样本分布参数可以选择，对于如何选择最优的分布参数将为本文今后的研究方向。

［1］杨志民，刘广利.不确定性支持向量机原理及应用［M］.北京:科学出版社，2007:35－40.

［2］VAPNIK V.The Nature of Statistical Learning Theory［M］.New York:Springer，1995:43 －49.

［3］BURGES C J C.A Tutorial on Support Vector Machines for Pattern Recognition［J］.Data Mining and Knowledge Discovery，1998，2(1):121 －167.

［4］MARTIN B，LEWIS H G，GUNN S R.Support Vector Machines For Spectral Unmixing［C］∥IGRASS’99，1999，2:1363－1365.

［5］HERMES L，FRIEAUFF D，PUZICHA Jan，et al.Support Vector Machines for Land Usage Classification in Landsat TM Imagery［C］∥Proc.of the IEEE International Geoscienceand Remote Sensing Symposium，1999，1:348－350.

［6］RANDEN T，JOHN H H.Filtering for Texture Classification:A Comparative Study［C］∥IEEE Trans.on Pattern Analysis and Machine Intelligence，1999，21(4):291－311.

［7］邓乃扬，田英杰.数据挖掘中的新方法:支持向量机［M］.北京:科学出版社，2004，6:42 －45.

［8］BURGES C J C.A Tutorial on Support Vector Machines for Pattern Recognition［J］.Data Mining and Dnowledge Discover，1998，2(2):106－112.