城市轨道交通节能线路仿真算法

杨利军，胡用生，孙丽霞

（同济大学 汽车学院，上海200092）

城市轨道交通与其他城市公共交通工具相比，具有运量大、安全舒适、快速环保、能源消耗少等优点，但由于城市轨道交通运量大，总耗电量仍相当大.根据轨道交通运营数据统计，车辆牵引用电占城市轨道交通用电量的50%以上，因此如何最大限度地优化列车的运营条件，降低能耗，成为各位专家学者重点研究的课题.南澳大利亚大学Howlett教授从20世纪90年代始，在节能运行优化理论方面进行了大量研究，并对干线机车／货车控制转换点以及坡道对操纵性能影响，进行了详细阐述［1－4］.国内方面，文献［5－7］从列车的操纵方法上进行了节能优化研究.由于城市轨道交通具有站间距短，坡度大，曲线半径小等特点，研究方法上有一定的特殊性.文献［8］根据这些特点，提出了适用于城市轨道交通的牵引控制算法.文献［9－16］从线路节能坡角度提出了节能概念并进行了探讨.

建立了多质点牵引计算模型，采用目标速度逼近算法求取牵引力撤除时间，既满足旅行速度又降低了运行能耗.提出了基于三角函数法设计节能线路纵断面竖曲线的设计方法，通过对线路坡度、坡长等参数进行优化，改变了列车的受力条件，实现势能和动能的合理转化，同时和列车的运行操纵相匹配，达到了优化节能的目的.

1 牵引计算模型

牵引计算采用多质点列车模型.由于考虑了列车的长度，在列车经过变坡点及变曲线点时，比单质点模型具有更高的计算精度.

1.1 列车多质点模型介绍

多质点模型以质点链来描述列车的受力状态，每一辆车视为一个质点，整列车是由多个质点构成的质点链.将质点间的联系视为刚性连接，整列车的运行状态取决于其受到的合力.多质点模型考虑了列车长度以后，可以计算车辆之间的相互作用力以及列车经过变坡段和曲线段时受力的实时变化情况.

1.2 变坡段列车受力分析

列车在变坡段受到附加阻力变化见图1.由图可知，当多质点列车经过线路变坡段时，由于各质点车辆C（m）在线路各点所处的位置不同，因此前后各车辆附加阻力也不同.

图1 列车在变坡段的附加阻力变化示意图Fig.1 Additional resistance on slope changeover section

每步计算时，先判断各质点车辆C（m）在线路上所处的位置及其对应的坡度（i），求出每节车辆上作用的坡道阻力G（m）＝mg×i，（mg为质点车辆的质量），最后得到列车的坡道附加阻力G，即

式中，N为列车包含的车辆数.

1.3 变曲率段列车受力分析

如图2所示，曲线段线路由直线段、缓和曲线段和圆曲线段组成［17］.不同区段上的曲率不同，直线段曲率为0，圆曲线段曲率为常数1／R.而在缓和曲线段上，曲率是变化的.假设缓和曲线的前半段为上凹抛物线（顶点在下）；后半段为下凹抛物线（顶点在上），缓和曲线（进／出）曲率沿轨道展开距离的函数表达式为

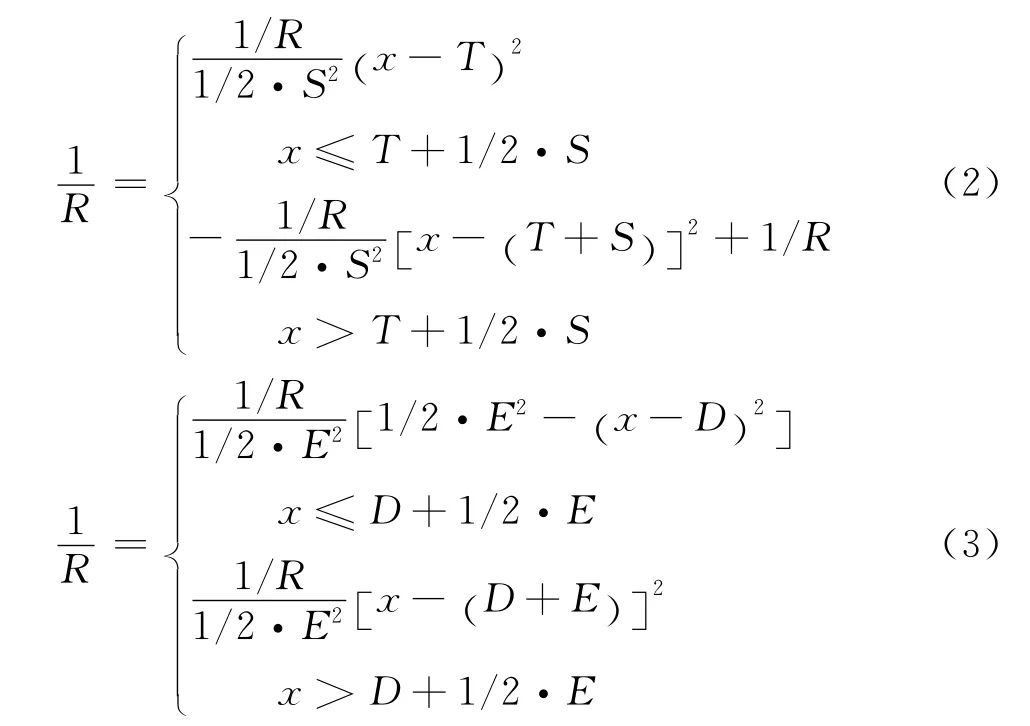
式中：T为直线段长度；S为缓和曲线（进）长度；C为圆曲线长度；E为缓和曲线（出）长度；D＝T＋S＋C

当多质点列车进入曲线时，由于不同位置对应的曲率不同，各质点车辆C（m）在线路各点所受的附加阻力也是不同的，R（m）＝mg×700／R.列车的坡道附加阻力R为各质点车辆附加阻力之和，如

图2 曲率随直线、缓和曲线、圆曲线变化关系Fig.2 Curvature on straight line，transition curve and circular curve

1.4 列车运行基本阻力

基本阻力是列车运行时与外界相互作用引起的阻力，如轴承摩擦阻力，轮轨相对运动阻力、空气阻力等.本文采用的阻力公式为修正了的戴维斯公式，为

式中：W（v）为列车基本阻力；M为列车重量；v为列车速度；n为轴数；N为车辆数；A为列车前端面积.

1.5 牵引计算方法

对于多质点模型，列车牵引计算公式为

式中：γ为列车回转质量系数；a为列车加速度；F（v）为列车牵引力，根据牵引特性曲线，采用插值法获得.

列车启动加速阶段牵引计算递推公式为

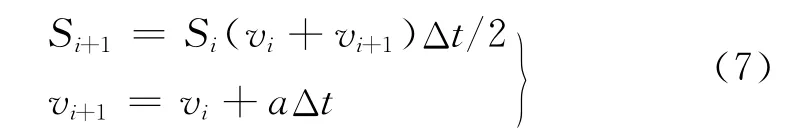
式中：S为列车运行距离；Δt为计算步长.

列车惰行时，牵引力F（v）去除，列车在阻力作用下运行.制动时，列车施加和运行方向相反的制动力b（v），使列车减速停车.

2 节能线路与节能操纵模式

2.1 节能运行原理

节能线路和节能运行模式的主要目标是通过线路设计和列车操纵方式，使列车运营所花费的能量最小，可以通过最优控制理论中的极小值原理来描述.

式中：状态矢量x（t）是n维分段光滑函数，控制矢量u（t）是m维分段连续函数，受式（10）约束.存在满足上述条件的最优控制矢量u＊（t），使以下性能指标泛函达到极小.

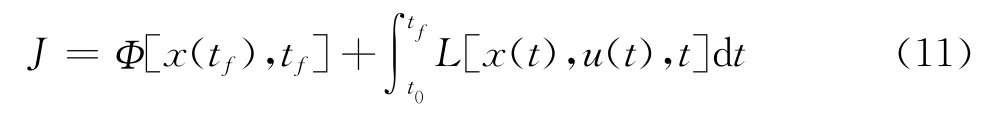
引入纯量函数H［x（t），u（t），λ（t），t］，定义为哈米尔登函数.

式中，λT（t）＝［λ1（t），λ2（t），…，λn（t）］为协状态矢量.

根据极小值原理，如果u＊（t）是最优控制，必然使哈米尔登函数沿着最优轨线达到极小.或者反过来说，使哈米尔登函数达到最小的控制就是最优控制.

线路纵断面设计时，可采用二维控制模型，分析求解能耗最小的列车运行方式.设两站间距为SR，根据式（6），建立列车的运行状态系统方程，如

式中：v为列车运行速度；s，h为列车质心坐标；fm（v）为即时速度最大单位牵引力；w0（v）为列车单位基本运行阻力；im为最大允许坡度；tRR为单位曲线阻力；u1＝i／im为坡度控制变量；u2＝f／fm为列车运行控制变量.控制变量满足以下约束条件

式中，uB为最大制动力与最大牵引力之比，uB＝bm／fm，bm（v）为最大单位制动力.

状态方程满足以下边界条件

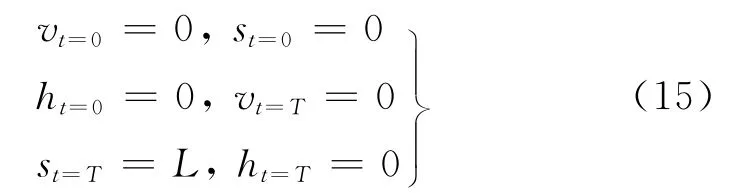
建立能耗最小的目标函数

式中，T为区间运行时分.

根据庞特里雅金最小值原理，u1、u2必须使哈密尔顿函数最小，为便于求解，将哈密尔顿函数改写，即等效于求式（17）的最大值.

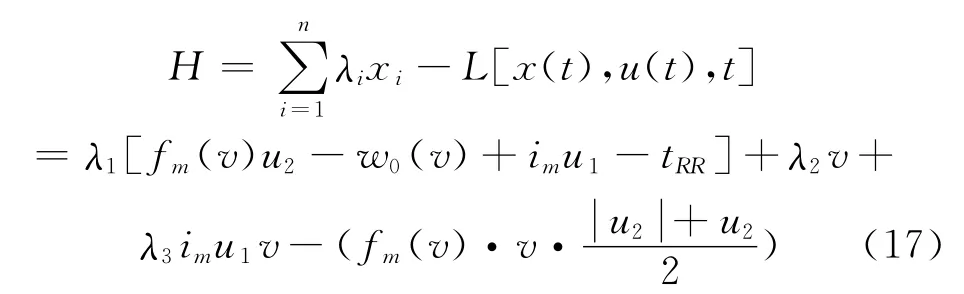
式中，λi为协状态矢量.

由式（14）和式（17），当哈密尔顿函数达到最大值时，控制变量u1和u2需按照下述条件取值

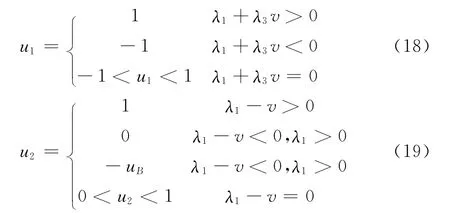
由式（18）可知，要满足能耗最小的运行要求，坡道最优控制由最大下坡道、过渡坡道和最大上坡道组成，即线路最佳断面形式为凹形纵断面.在坡道轨迹形状确定后，可通过设定合理的坡道转换点（坡道长度和坡度）来降低能耗.由式（19）可知，列车运行最优控制为最大牵引、恒速、惰行和最大制动组成.牵引能耗主要发生在列车出站牵引区段，要使列车在较小的能耗条件下尽快加速到恒速区段，可以利用节能坡进行辅助加速.根据不同坡度和坡长，并结合列车的实际载重条件，选定最佳的牵引力施加和撤除时间转换点，以达到以低能耗满足运营需求的目的.

2.2 节能线路纵断面的竖曲线设计方法

线路节能设计要合理选择车站区间坡度及坡长，使车辆在出站时通过区间下坡迅速地将重力势能转化为动能，在尽可能少耗费牵引电能的情况下，获得列车运行所需要的加速度和目标速度［14，16］；车辆进站之前通过站前上坡将车辆动能转化为势能，降低列车制动前的速度，缩短制动时间，尽量减少制动能耗.

提出的节能线路综合考虑了牵引节能操作序列和节能线路纵断面设计原则，将节能线路分为5个区段，依次为“牵引出坡坡段—惰行下坡坡段—匀速运行段—惰行上坡坡段—制动进站坡段”，见图3.列车在整条线路上的运行过程与列车牵引节能的操作思想相吻合.

图3 节能坡区间分段示意图Fig.3 Energy conservation section

线路纵断面设计采用坡度渐变的正、余弦三角函数形状坡段，将站台与匀速段有效连接起来.这种设计可以使节能坡道尽量靠近车站，竖曲线头贴近站台端部，发挥最大节能效果.和竖曲线－直线坡道连接方式相比，衔接更为紧密，过渡更为平缓.列车在线路上运行时位置坐标如

式中：H为坡道高度；L为坡道长度；Sp为列车运行起始点与下坡点距离；SR为站间距；S为列车运行位置线路横坐标；ydown和yup为下坡段和上坡段列车位置纵坐标.

下坡段和上坡段各点坡度为位置坐标的导数，即y′down和y′up.

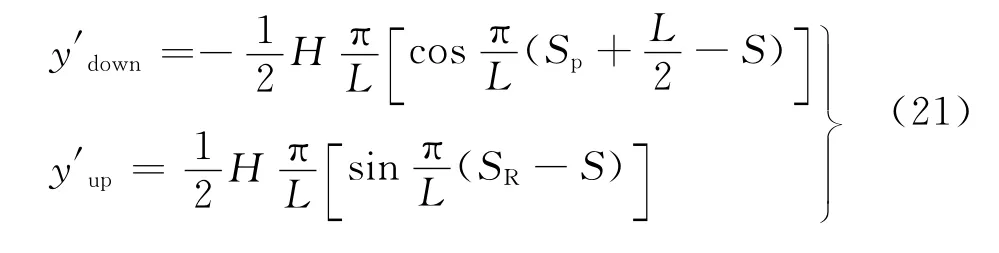
3 节能仿真算法

3.1 目标逼近算法

根据前面提到的牵引控制策略，列车启动出站后，先采用最大牵引力牵引出坡至图3中A点位置，然后从A点惰行到坡底匀速临界点B.之后以速度Vmax匀速运行至C点后，改惰行上坡，D点位置开始施加制动停车.

纵观整个区间运行，工况转换点A点位置的选取至关重要，直接关系到列车的运行能耗.采用目标速度逼近算法来精确确定A点的位置.

首先设定B点所要达到的最大速度Vmax，BC段的速度即为Vmax.然后，采用反推法，以Vmax为初速度逆着AB方向上坡，直到找到牵引工况和惰行工况的转换点A为止.

Vmax的确定受到整个运行过程所要达到的平均速度Vn（也称技术速度）约束，Vn的值是根据运营需求事先确定的.Vmax与Vn之间是非线性关系，采用牛顿法求解.

首先，假定Vn＝F（Vmax），根据全微分概念，得离散化的表达式

式中：（Vmax）n为第n次迭代的最大速度；（Vn）n为第n次迭代的平均速度.先给（Vmax）0设定一个初始值，经过计算和反复迭代，便可以向目标值Vn逼近.同理，给定运营要求的Vn，经过反迭代，可以求出B点所需的Vmax，从而求出转换点A所处的位置.

列车以速度Vmax匀速运行至C点后，改惰行上坡，制动临界点D的选取与A点的选取方法一致，采取从进站点开始以0为初速反向运行的方法逼近.

3.2 计算流程

线路运行情况模拟通过列车牵引仿真软件来实现，目标速度逼近算法计算流程见图4.

图4 目标速度逼近计算流程Fig.4 Target velocity approaching arithmetic

4 仿真案例

选取上海市轨道交通八号线“延吉中路站——黄兴路站”进行节能线路纵断面设计分析计算，该段线路为地下线，两站的站间距为1.31km，高差很小，可以视为等高.图5为两站之间的纵断面示意图.

图5 纵断面示意图（坡长单位为m，坡度单位为‰）Fig.5 Longitudinal section of track profile（slope length m，gradient‰）

由于节能线路设计与列车编组、车辆性能和最大运行速度等有关.列车取6节编组，动拖比为2：1，采用AW2工况，列车重量为287.6t.动车及拖车车长均按19.5m计，整列车长117.0m，站台长取为140.0m.

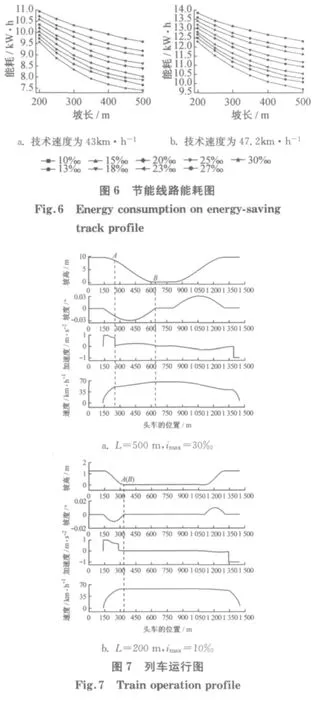
根据仿真计算，在延吉中路站到黄兴路站实际线路的计算能耗为12.86kW·h，运行时间为1.67 min，技术速度可达47.2km·h－1.于是，整个运行过程所要达到的技术速度Vn选取为47.2km·h－1，若停站时间为25s，则列车在该技术速度下的旅行速度为37.7km·h－1.考虑到地铁车辆不小于35km·h－1的旅行速度要求，给出了旅行速度恰为35km·h－1（技术速度为43km·h－1）时的运行能耗进行对比.

将节能坡参数代入仿真软件进行计算，列车在技术速度为43和47.2km·h－1，不同纵断面节能线路的运行能耗见图6.其中最大坡度imax‰值为10‰、13‰、15‰、18‰、20‰、23‰、25‰、27‰、30‰，坡长取值200～500m.当技术速度为47.2 km·h－1时，图中大部分坡长及坡度组合的能耗都小于12.86kW·h，可见，该节能坡具有明显的节能效果.

技术速度为47.2km·h－1时，坡长L＝500m，最大坡度imax＝30‰和坡长L＝200m，最大坡度imax＝10‰两端线路进行对比分析，列车的运行情况见图7.

由图可知，L＝500m，imax＝30‰时，列车出坡牵引至图示A点即改为惰行，列车在图7a的AB段上处于惰行工况，利用节能坡将势能转化为坡底的动能，列车开始制动的初速为40km·h－1，节约能耗为9.69kW·h.而当L＝200m，imax＝10‰时，由于节能坡道短，坡度小，列车为了达到技术速度要求，在整个节能坡段几乎处于牵引工况，惰行工况转换点A和下坡匀速临界点B几乎重合，不经惰行工况转化即进入匀速坡，几乎没有发挥节能坡的作用，列车开始制动的初速为54km·h－1，因此能耗较大，为13.85kW·h.

综合分析以上列车在不同技术速度下的运行能耗，可以得出以下结论：

（1）在给定的坡长及坡度范围内，坡长一定时，随着坡度的增加，能耗逐渐减少；当最大坡度一定时，能耗随坡长的增加同样呈现降低的趋势.

（2）技术速度从43km·h－1增大至47.2km·h－1时，能耗增加了26.6%～31.76%，节能坡的合理长度与坡度和列车运行的目标技术速度有关.

（3）节能坡的坡度和坡长设置，需要和列车的牵引性能综合起来考虑.在线路设计时，通过牵引仿真程序，对各种线路工况和列车配置进行计算，在满足运营要求条件下，选择合理的坡度和坡长，充分发挥节能坡辅助牵引作用，以降低车辆的配置成本和能耗，提高经济效益.

5 结语

通过对上海市轨道交通八号线“延吉中路站——黄兴路站”进行的节能线路运行能耗计算，验证了节能线路纵断面的竖曲线设计方法和牵引仿真软件的有效性.节能线路坡段长度和坡度需根据列车编组、车辆加减速性能、列车最大运行速度等进行设置.节能坡优化设计和列车牵引动力配置相结合，可实现系统优化配置，有利于轨道交通系统的可持续发展.

［1］Chen J，Howlett P.A note on the calculation of optimal strategies for the minimization of fuel consumption in the control of trains［J］.Transactions on Automatic Control，1993，38（11）：1730.

［2］Howlett P.Optimal strategies for the control of a train［J］.Automatica，1996，32（4）：519.

［3］Howlett P.The optimal control of a train［J］.Annals of Operations Research，2000（98）：65.

［4］Howlett P，Pudney P J，Vu Xuan.Local energy minimization in optimal train control［J］.Automatica，2009（45）：2692.

［5］金炜东，王自力，李崇维，等.列车节能操纵优化方法研究［J］.铁道学报，1997（06）：59.JIN Weidong，WANG Zili，LI Chongwei，et al.Study on optimization method of train operation for saving energy［J］.Journal of the China Railway Society，1997（06）：59.

［6］丁勇，毛保华，刘海东，等.定时约束条件下列车节能操纵的仿真算法研究［J］.系统仿真学报，2004（10）：2241.DING Yong，MAO Baohua，LIU Haidong，et al.An algorithm for energy－efficient train operation simulation with fixed running time［J］.Journal of System Simulation，2004（10）：2241.

［7］刘海东，毛保华，丁勇，等.列车自动驾驶仿真系统算法及其实施研究［J］.系统仿真学报，2005（3）：577.LIU Haidong，MAO Baohua，DING Yong，et al.A study on simulation algorithm and operation of automatic train operation［J］.Journal of System Simulation，2005（3）：577.

［8］石红国，彭其渊，郭寒英.城市轨道交通牵引计算算法［J］.交通运输工程学报，2004（03）：30.SHI Hongguo， PENG Qiyuan， GUO Hanying.Traction calculatio of urban mass transit［J］.Journal of Traffic and Transportation Engineering，2004（03）：30.

［9］赵中旺，金德银.对铁路最佳节能纵断面形式的研究［J］.石家庄铁道学院学报，1999（1）：82.ZHAO Zhongwang，JIN Deyin.The study on the optimal railway vertical section model for energy consumption［J］.Journal of Shijiazhuang Railway Institute，1999（1）：82.

［10］何永春.轨道交通中的节能坡及其工程应用［J］.城市轨道交通研究，2003（2）：37.HE Yongchun.Energy saving vertical section in rail transit［J］.Urban Mass Transit，2003（2）：37.

［11］刘海东，毛保华，丁勇，等.城市轨道交通列车节能问题及方案研究［J］.交通运输系统工程与信息，2007（5）：68.LIU Haidong，MAO baohua，DING Yong，et al.Train energysaving scheme with evaluation in urban mass transit system［J］.Journal of Transportation System Engineering and Information Technology.2007（5）：68.

［12］庞渊.线路节能坡设计方案对地铁能耗的影响［J］.铁路工程造价管理，2008（1）：10.PANG Yuan.Impacts of line’s energy saving slope design scheme on energy consumption of metros［J］.Railway Engineering Cost Management.2008（1）：10.

［13］桂翔.城市轨道交通牵引计算仿真系统的研究和开发［D］.北京：北京交通大学土木建筑工程学院，2008.GUI Xiang.Research and development of urban rail transit traction calculation system［D］.Beijing：Beijing Jiaotong University.Civil engineering and architecture institute，2008.

［14］乐建迪.地铁正线节能坡设计探讨［J］.铁道标准设计，2008（8）：17.LE Jiandi.Study of energy－saving slope design on metro line［J］.Railway Standard Design，2008（8）：17.

［15］付印平.列车追踪运行与节能优化建模及模拟研究［D］.北京：北京交通大学交通运输规划与管理学院，2009.FU Yinping.Research on modeling and simulations of train tracking operation and saving energy optimization［D］.Beijing：Beijing Jiaotong University.Transportation Planning and Management Institute，2009.

［16］周斌，袁江，丁静波.广州地铁3号线北延段工程线路节能坡设计［J］.铁道标准设计，2009，（7）：14.ZHOU Bin，YUAN Jiang，DING Jingbo.Design on energysaving slope profile of Guangzhou metro line 3Ext North［J］Railway Standard Design，2009（7）：14.

［17］张定贤.机车车辆轨道系统动力学［M］.北京：中国铁道出版社，1996.ZHANG Dingxian.Railway system dynamics of locomotive and rolling stocks［M］.Beijing：China Railway Press，1996.