基于风险分析的交通事件持续时间预测

康国祥，方守恩

（同济大学 道路与交通工程教育部重点实验室 上海200092）

交通事件（如交通事故、车辆抛锚、天气状况等）是造成高速公路交通拥堵的主要原因之一.一些研究表明［1－2］，高速公路交通事件引起的偶发性交通拥堵占总拥堵的50%～75%.实践证明，交通事件造成的延误大小在很大程度上取决于事件处理过程，事件发现时间、反应时间以及清除时间越短，它对道路交通流的影响就越小.然而，对于交通管理者而言，最困难的一步是要预估交通事件的持续时间，预估准确，才能有助于决定采取何种有效的管理措施和交通转移策略.另外，预估准确的交通事件持续时间信息的发布还可以使交通出行者改变行车路线或者重新规划他们的出行计划.

目前，最常用的事件持续时间预测方法是基于风险分析 的 方 法［3－5］、回 归 分 析 方 法［6－8］和 决 策 树 方法［9－11］.基于风险分析的交通事件持续时间预测是一种条件概率的方法，相比于其他研究方法，它可以更好地处理因事件结束时间删失导致的信息残缺数据，扩大了可利用的交通事件数据的范围，并且可以定量地分析观察指标的作用强度和方向.本文首先介绍了交通事件持续时间的定义和构建基于风险分析的持续时间预测模型，接着对所用数据进行了描述，然后对建立的预测模型进行参数估计和预测精度检验，最后进行了总结并提出了未来进一步研究的建议.

1 基于风险分析的交通事件持续时间预测模型

1.1 交通事件持续时间

交通事件持续时间是指从交通事件发生到交通恢复到正常状态的总时间，可分为四个阶段，如图1所示.由于第四个阶段是不可控制的变量，受各种因素的影响而变得比较复杂，并且在实际较难获得关键信息，因此本文研究的交通事件持续时间仅包含前三个阶段，即从事件发生至现场清除完毕，救援车辆离开时所经历的时间.

图1 交通事件持续时间的四个阶段Fig.1 Components of accident duration

1.2 模型的建立

基于风险分析的持续时间是指从某个起始事件开始到某个终点事件发生所经历的时间，也称失效时间.某个具体交通事件的持续时间是一个随机变量，用T表示.基于风险的持续时间模型就是采用条件概率的思想，分析一个已经持续了tmin的事件在第t＋Δtmin结束的概率，这个条件概率h（t）被称为风险函数（Hazard Function，HF）.

基于风险的持续时间模型可以通过四个函数来描述：分布函数F（t），概率密度函数f（t），生存函数S（t），风险函数h（t）.四个函数之间的关系如下：

一次交通事件的持续时间为T，它小于一个定值t的 概率为F（t）：

F（t）是可微的，其概率密度函数为f（t），表示一次交通事件在t～t＋Δt这一微时段内结束的概率，可表示为

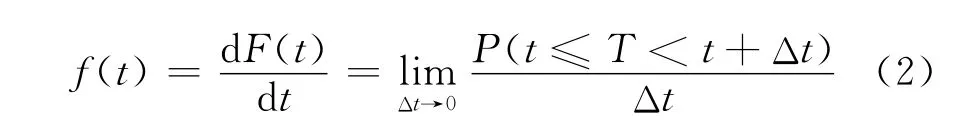
生存函数S（t）表示一次交通事件持续时间长于t的概率，可表示为

风险函数h（t）指t时刻仍未结束的交通事件在t时刻后一瞬间结束的概率，为条件概率，即交通事件持续了t时刻的条件下在t～t＋Δt这一微时段内结束的概率，其表达式为

如果风险函数的导数dh（t）／dt大于0，则风险函数值随时间的增加而增加，表示若事件尚未结束，则预示着事件会很快被清除；如果风险函数值的导数dh（t）／dt小于0，则风险函数值随时间的增加而减小，预示事件可能仍将持续一段时间，不会立刻结束；如果风险函数值的导数dh（t）／dt等于0，则说明事件结束时间的概率与时间变量无关.

比例风险（proportional hazard，PH）模型和加速失效时间（accelerated failure time，AFT）模型是两种比较常用的基于风险的持续时间预测方法.两种方法都可以用来分析解释变量对持续时间概率的影响，前者不需要对理论分布做任何假设，是一种半参数的估计方法，后者是一种参数估计方法，通常假定持续时间服从特定的参数分布，根据分布的特点对影响持续时间的变量进行分析，常用的方法有指数分布法、Weibull（威布尔）分布法、Log－normal（对数正态）回归分析法和Log－logistic（对数逻辑斯蒂）回归分析法等.为了进行持续时间预测，参数模型比半参数模型更为准确.如图2所示，将所用数据的概率分布图与特定分布的概率图进行比较发现，Weibull分布比较结果呈线性关系.因此，Weibull AFT（威布尔加速失效时间）模型更为适合本文数据进行交通事件持续时间的预测.

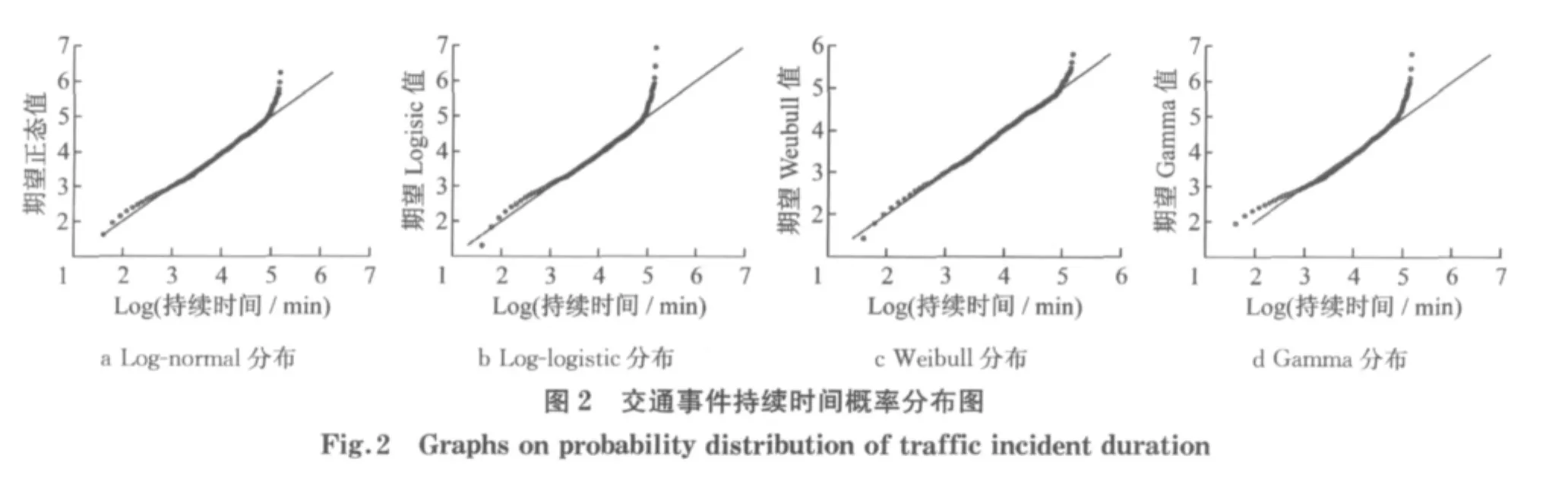
除已引入变量外，由于持续时间的影响因素较多，故引入异质性参数γ，以验证是否仍存在未知因素可能会对风险函数形状及其协变量系数产生较大影响，一般假设γ服从Gamma分布.考虑Gamma异质性的Weibull AFT模型的风险函数表达式为

式中：P为形状参数，决定分布函数的形态，当P＝1时，危险率是常数.当P＞1时，危险率随时间增大而增大，P＜1时危险率随时间增大而减小；λ为尺度参数，决定分布函数的分散度，尺度参数λ＝exp（β0＋βX1＋…＋βmXm），Xi（i＝1，2，…，m）为危险因素，β0为截距，βi为危险因素的回归系数；θ是异质性参数γ的方差，当不存在异质性时，即不存在未知因素对模型产生较大影响，θ值接近于0.

2 数据描述

所使用数据来源于浙江省嘉兴市高速公路应急救援指挥中心管理系统，该中心承担着辖区内高速公路上交通事件的报警、求助、施救、投诉、信息发布等工作，并详细记录高速公路养护、交通事件处置等相关信息.选择与目前处理事件的条件差异不大的数据来标定模型，以减少数据的离散性，避免了由于数据离散本身对模型精度的影响.所分析的交通事件数据是2006—2008年近3年双向8车道高速公路上发生的交通事件，见表1，选取了1 327组有效数据进行研究，将样本随机分为两部分，一部分用于风险模型的标定，标定数据为1 062个，占样本总数的80%，另一部分验证风险模型，共265个数据，占样本总数的20%.

表1 用于标定和验证的交通事件数据的描述性统计Tab.1 Descriptive statistic of traffic incident data for validation and calibration

每组数据由事件的持续时间和可能影响事件持续时间的因素构成，这些因素大致分为以下几类：事件时间信息，如发生时刻、日、月、删失状态；事件基本信息：事件类型、涉及车辆类型、严重程度（如涉及车辆数量、人员死亡和受伤人数）、发生位置；环境状况，如天气、道路表面状况、工作区、是否有车辆停靠在路肩；事件信息来源，如报警人类型；救援车辆信息，如是否需要救护车、牵引车、吊车等.由于影响因素较多，只有那些更直观、更易获得的显著信息才会被用到模型构建当中.取显著水平α＝0.05，通过影响因素显著性分析最终获得除删失状态外的15个显著因素（P＜0.05），而删失状态仅作为状态变量引入，不作为影响因素考虑，见表2，并将这15个因素作为初始变量进行模型的参数估计.

表2 交通事件持续时间的显著影响因素Tab.2 Significant influence factors of traffic incident duration

3 模型的估计和检验

运用上述基于风险分析的方法，利用R软件进行Weibull AFT持续时间模型的参数估计，结果见表3.从表3中可以看出：

（1）形状参数P＞1（P＝1.809 4），这表明危险率随时间增大而增大，见图3.θ值接近于零，说明不存在未知因素对模型参数和风险函数产生较大影响.

（2）只有截距、变量如夜晚、报警人类型、事件类型、占用车道数、涉及车辆数、人员死亡、救护车、牵引车、吊车、驳载车、涉及货车对持续时间影响有非常显著性意义，其他变量均无显著性（显著性水平取α＝0.05）.

表3 考虑gamma异质性的Weibull AFT持续时间模型估计结果Tab.3 Estimated results of Weibull AFT model for incident duration with gamma heterogeneity

图3 Weibull AFT持续时间模型风险函数图Fig.3 Hazard function plot of Weibull AFT model for incident duration

（3）因事件类型是分类变量，它有5个水平，当拟合参数模型时，自动将最后一个水平（着火事件）作为参照分类对比，追尾事件、翻车事件、抛锚事件、碰撞固定物事件相比着火事件均具有显著性差异（显著性水平取α＝0.05），并且这四种事件的持续时间都比着火事件短（其标志为回归系数为负值）.

（4）变量报警人类型的回归系数为负值，表明该因素相对危险度在降低，即报警人为交通管理者（变量赋值为1）时，相对于驾驶员报警（变量赋值为0），减少了事件持续时间，这是因为交通管理者可直接开展现场救援工作，略去了事件发现和响应阶段；其它变量的回归系数为正数，表明因素相对危险度增加，即该因素变量赋值为1时，事件严重程度或者施救难度增大，相比于变量赋值为0，延长了事件持续时间.

为了验证模型的有效性，采用用于验证的265个交通事件数据进行检验，结果见图4.从图4中可以看出：持续时间小于10min的抛锚事预测精度较差，对抛锚事件整体预测精度有较大影响，因为持续时间小于10min的抛锚事件一般是一些小的故障造成的，其持续时间受驾驶员维修能力等随机性因素影响较大；在只考虑持续时间大于10min抛锚事件时，其持续时间预测误差小于10min的准确率为70%；而在交通事故中，持续时间小于10min的事故比例较低，其预测误差对整体预测精度影响不大，可忽略不计，所以交通事故预测持续时间预测误差小于30min的准确率为78%.由于本文中交通事件发生在城市间高速公路，距离医疗急救点、医院、消防部门等较远，救援车辆施救距离较长，因此预测准确率相对于事件平均时间（交通事故平均持续时间为56.9min，抛锚事件平均持续时间为31.1min）来说是可以接受的.同时，这一预测精度比贝叶斯方法［12］和决策树方法［13］的预测精度有所提高.

图4 事件持续时间的实测值与预测值Fig.4 Real value and prediction value of incident duration time

4 结语

对沪杭高速公路嘉兴段1 327个交通事件数据进行了分析，其中1 062个数据用于建立基于风险分析的Weibull AFT模型，265个数据用于检验模型的预测精度.夜晚、报警人类型、事件类型、占用车道数、涉及车辆数、人员死亡、救护车、牵引车、吊车、驳载车、涉及货车等11个变量是影响交通时间持续时间的显著性因素.预测结果表明，持续时间小于10 min的抛锚事件的预测精度较差，其预测精度受驾驶员维修能力等随机性因素影响较大；当只考虑持续时间大于10min抛锚事件时，其持续时间预测误差小于10min的准确率为70%；而交通事故持续时间预测误差小于30min的准确率为78%.预测准确率相对于事件平均时间来说，是可以接受的.但由于事件处理人员的业务水平存在较大的差异，仍可能导致一些事件的预测值和实际值之间存在较大的误差.

不同车道数的高速公路上发生交通事件时，由于车辆占用车道数量不同，导致高速公路路段剩余通行能力是不同的，这可能会影响模型的引入变量数量和预测精度的差异.本文所用的交通事件数据和建立的持续时间预测模型来自于双向8车道高速公路，由于浙江省嘉兴市辖区内的双向6车道高速公路上的交通事件数据由于数量较少，并未纳入到本文模型的构建和验证之中.虽然每条高速公路的环境条件以及信息来源不同，但是在方法论上对双向4车道、双向6车道高速公路上的事件持续时间预测研究仍具有普遍适用性.因此，双向4车道、双向6车道高速公路的风险分析模型将作为本研究进一步深化的方向，可与双向8车道风险分析模型进行比较研究.相比于其它的研究方法，基于风险分析的预测方法不仅可对具有完整持续时间的事件进行预测，还可处理因事件结束时间删失导致的持续时间残缺值数据，扩大了可研究的交通事件数据的范围，在定量分析观察指标的作用强度和方向的基础上，提高了预测的精度.同时，交通管理者只有在充分了解交通事件的性质、严重程度和道路状况，准确地预估交通事件持续时间的基础上，才能提出行之有效的事件处置方案，如人力、物力和技术资源的合理使用，以及交通控制策略，在最短的时间范围内完成事件管理的各项活动，减小事件的影响，使受到干扰的交通流恢复正常.

［1］Giuliano Genevieve.Incident characteristics，frequency，and duration on a high volume urban freeway［J］.Transportation Research Board，National Research Council：Transportation Research Part A，1989，23（5）：387.

［2］Stathopulos A，Karlaftis M G.Modeling duration of urban traffic congestion［J］.Journal of Transportation Engineering，2002，128（6），587.

［3］Doohee Nam，Fred Mannering.An exploratory hazard－based analysis of highway incident duration［J］.Transp Res，2000，34A （2）：85.

［4］Zografos K G，Konstantions N A，George M V.A real－time decision support system for roadway network incident response logistics［J］.Transportation Research.Part C.2002，10（1）：1.

［5］CHUNG Younshik.Development of an accident duration prediction model on the Korean Freeway Systems［J］.Accident Analysis and Prevention.2010，42：282.

［6］Garib A，Radwan A E，Al－deek H.Estimating magnitude and duration of incident delays［J］.Journal of Transportation Engineering.1997，123（6）：459.

［7］Edward C S.New model for predicting freeway incidents and incident delays［J］.Journal of Transportation Engineering.1997，123（4）：267.

［8］刘伟铭，管丽萍，尹湘源.基于多元回归分析的事件持续时间预测［J］.公路交通科技，2005，22（11）：126.Liu weimiing，Guan liping，Yin xiangyuan.Prediction of Incident Duration Based on Multiple Regression Analysis［J］.Journal of Highway and Transportation Research and Development，2005，22（11）：126.

［9］Ozbay K，Narayanan A.Jonnalagadda S.Wide－area incident management support system （WAIMSS）［C］／／3rd Annual World Congress on ITS.Orlando：IT’S America.1996：14－18.

［10］Ozbay K，Kachroo P.Incident management in intelligent transportation systems［M］.London：Artech House.1999.

［11］姬杨蓓蓓，张小宁，孙立军.基于贝叶斯决策树的交通事件持续时间预测［J］.同济大学学报，2008，36（3）：319.JIYANG Beibei，ZHANG Xiaoning，SUN Lijun.Traffic incident duration prediction grounded on bayesian decision methodbased tree algorithm.［J］Journal of Tongji University：Natural Science，2008，36（3）：319.

［12］Boyles S，Fajardo S T.Waller.A naïve Bayesian classifier for incident duration prediction ［C／OL］／／［S.l.］Transportation Research Board Annual Meeting，2007［2006－7－31］.http：／／www.uwyo.edu／sboyles／research／boyles fajardo waller nbc.pdf.

［13］姬杨蓓蓓.交通事件持续时间预测方法研究［D］.上海：同济大学交通运输工程学院，2008 JIYANG Beibei.Research on prediction method of traffic incident duration［J］.Shanghai：College of Transportation Engineering of Tongji University，2008.