随机波动率下信用风险定价模型的比较分析
郭培栋,陈启宏
0 引言
在可违约债券研究中,由以往的文献可以知道可违约债券的风险主要来自三个方面,即违约风险、利率风险、市场风险(波动率风险)。在经典的信用风险模型——结构化模型和约化式模型——中主要考虑的是违约风险和利率风险。上述信用风险定价模型的一个共同的特点就是都假设在资产价值的波动率是常数的基础上进行讨论的,而没有考虑到波动率风险。由于假定波动率是恒定的,因此在估计波动率的时候直接把过去的波动率估计值看作未来波动率预测值,这种简单而又直接的估计通常与实际情形有很大的偏差,成为一种最不准确的一种波动率测量和预测工具。显然,波动率在时间序列上不可能是一个常数,而是一个动态随机过程,这点在资产回报的时间序列和通过B-S模型的期权市场价格隐含的波动率的实证检验中证实。
随机波动率模型最早是用来定价期权等信用衍生产品[1-3]。后来在信用风险定价模型也逐步引入随机波动率因素,由于随机波动率的引入使得模型变得更复杂,因此在给公式债券定价的时候往往都是考虑它的数值解或近似解。Jean-Pierre Fouque,Ronnie Sircary和Knut Solna[4]在首次通过结构模型(First passage structural approach)引入随机波动率模型,并分析了波动率对信用价差的影响,在这里还讨论了刻划随机波动率的多因子模型。陈侃和李时银[5]讨论了随机波动率下可违约债券的定价,在假设标的资产价格的波动率是一个快速均值回复OU过程的函数的条件下,利用Taylor级数展开得到非完全市场下固定补偿率的债券价格的近似表达式。在信用风险定价模型中考虑波动率的随机性有很重要的意义。首先,作为一个投资公司债务的投资者,他必须要关注公司偿还债务的风险,即公司的破产概率,公司资产价值的波动率是影响破产概率的一个重要变量;其次,从投资者的角度来看,利差收益是他们投资的主要收益,虽然不可否认影响利差的因素众多,但公司资产价值的波动率显然是其中的一个重要因素。
本文将讨论在随机波动率假设下,在利率分别为常数和随机情形下可违约债券的定价问题。这里主要在结构法的三种经典模型下——Merton模型、跳扩散模型和首次通过模型——来讨论的。本文还将利用特征函数得到了可违约债券价格和公司违约概率的显式表达式,并通过数值模拟分析随机波动率对信用价差和违约概率期限结构的影响。
1 Merton模型
基本假设:
(1)无风险利率r为常数。
(2)公司资产的价格V(v,t)满足动态过程

其中μ为常数,W1为标准维纳过程。
(3)波动率状态变量vt服从扩散过程

其中,参数k,θ,σ都为常数,W2为标准维纳过程。
(4)Cov(dW1,dW2)=ρ1dt,其中ρ1为常数,表示两个布朗运动的相关系数。
(5)市场是无摩擦的。
(6)满足Merton模型的其它假设。
记公司的债务为F,则在债券到期日债权人的收益为
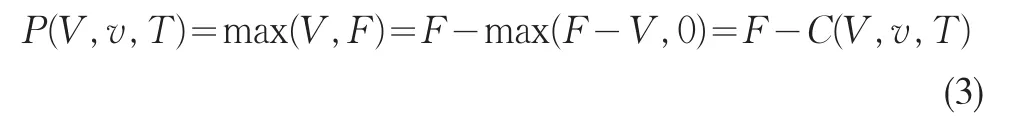
这里的C(V,v,T)表示基于公司资产的欧式看跌期权在到期日的收益,对于欧式看跌期权C(V,v,t)满足方程
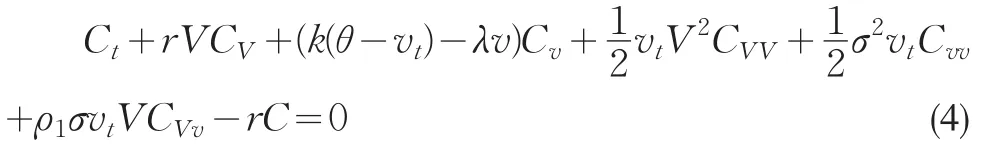
根据波动率为常数时的欧式看跌期权的定价公式,可以假设
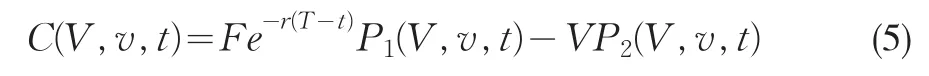
作变换x=lnV,把式(5)代入式(4)可得P1和P2满足方程
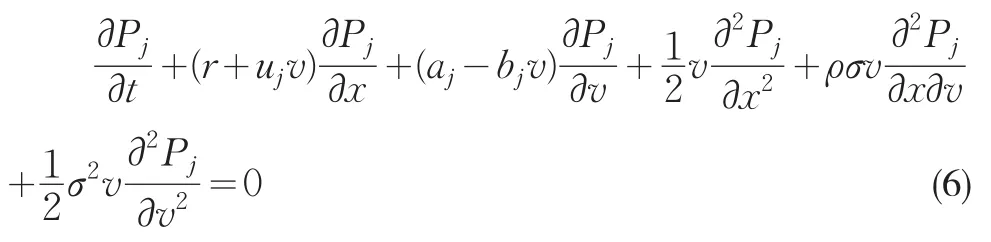
上式中λ2,此时相应的参数分别为:
u1=-1/2,u2=1/2,a1=a2=kθ
b1=k+λ,b2=k+λ-ρ1σ
此时P1和P2满足的终值条件为:
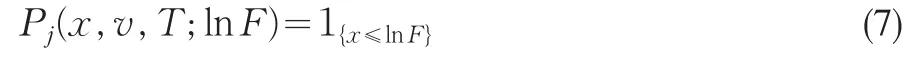
这里Pj就可看作在期权到期日变量x≥lnK的概率了。现在我们来求解式(6),为此不妨先设
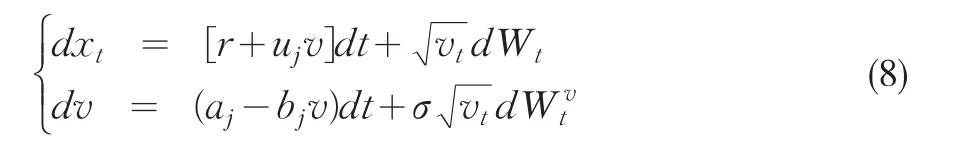
其中参数aj,bj,uj与式(6)一样。考虑函数V(S,M,τ)≤VA(S,M,τ)<VA(αM,M,τ)+(αM-S)+≤ δ+(αM-S)+. ,对于V(S,M,τ)=VA(S,M,τ),令τ*=T为δ=VA(S,M,τˉ)在期权到期时刻的条件期望,即:
由Ito引理可得:
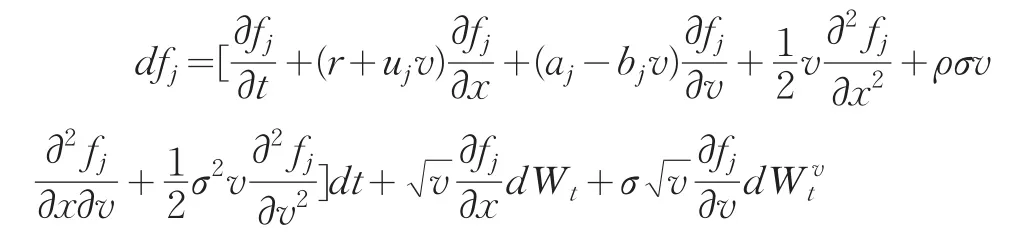
由期望的迭代法则可知,fj必为鞅,从而可得dt项的系数为零,故有:
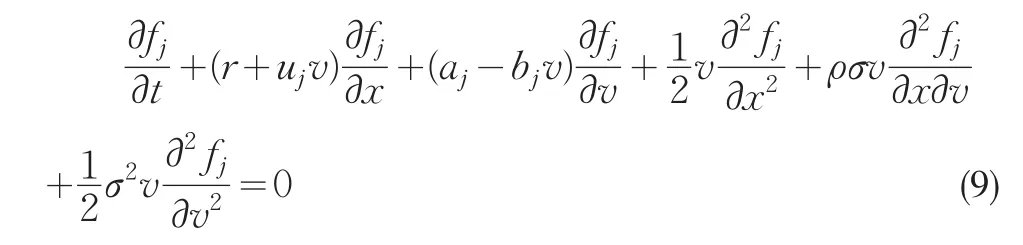
fj满足的终值条件为
若记S0∈(αM,∞),则(αM,∞)与S=αM满足的方程和终值条件完全一致,故δ也可看作是一个关于的条件期望,即(S,τ)。

特征函数有如下形式的解:

记τ=T-t,把(11)代入(9)、(10)可得C(τ;ϕ),D(τ;ϕ)满足方程
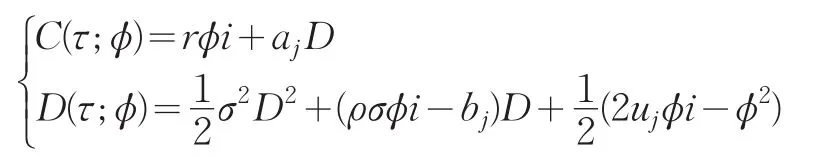
解之可得:
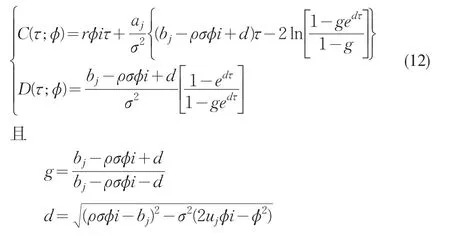
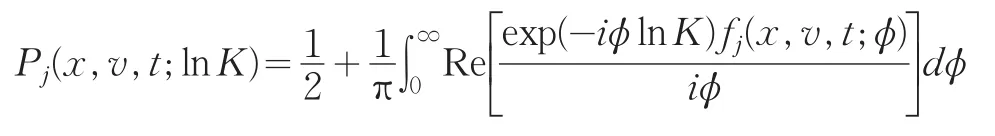
通过对特征函数作逆变换就可得概率函数Pj的表达式为:利用特征函数及其逆变换,同理可得Pj(j=1,2)的表达式为:
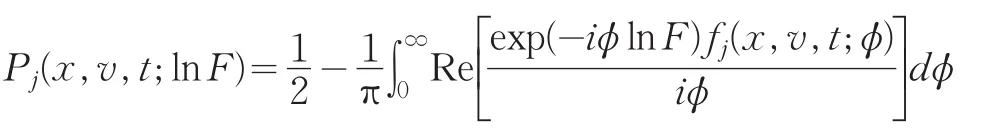
其中fj(x,v,T;lnF)满足式(11),(12)。由(3)可知债券价格等于债务的无风险贴现减去一个基于公司资产的看跌期权的价格,即
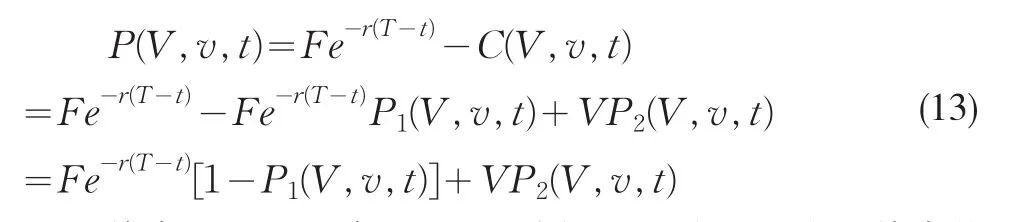
债券的违约概率:上面的分析已经给出了公司债券价格公式,把其各项进行重新整理,则有
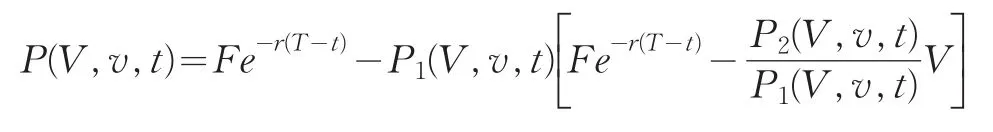
那么P1(V,v,t)就表示在[t,T]内债券违约概率,中挂号中的项表示违约时预期的贴现损失。
由上述债券定价公式可以得到信用价差的表达式,信用价差定义为可违约债券与不可违约债券收益率的差异,因此有
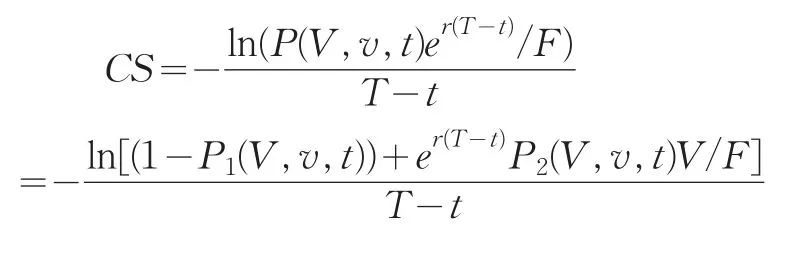
2 跳扩散模型
在风险中性下假设公司资产价格的动态过程为:
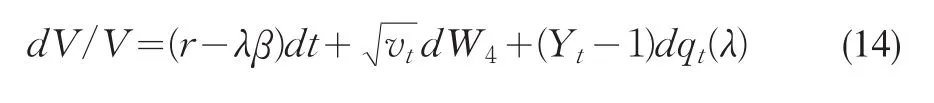
波动率状态变量vt满足微分方程(2),其中qt(λ)表示强度为λ的poisson过程,用来刻划在时间段[t,t+dt]内跳跃发生的次数,Yt∈(0,+∞)是独立同分布的随机变量,表示一旦跳跃发生时,跳跃的幅度,且Yt和qt(λ)是相互独立的,且独立于维纳过程W2和W4。维纳过程W2和W4是相关的,且有Cov(dW2,dW4)=ρ2dt。在跳扩散假设下,欧式期权的价格C(V,v,t)满足方程

期权价格满足终值条件C(V,v,T)=max(F-VT,0),期权的价格C(V,v,t)的表达式可记为:

与前一样,这里Π1和Π2表示在期权到期日F>VT的条件概率。现在我们先求出它们的特征函数,再通过逆变换得到Π1和Π2的解。作变换x=lnV,记此时它们的特征函数为可得满足的方程为:

令
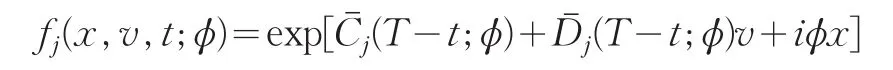
代入式(17)、(18)可得
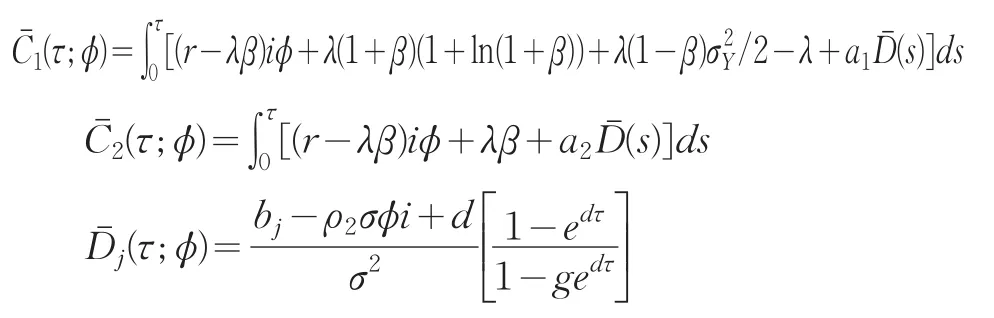
其中:
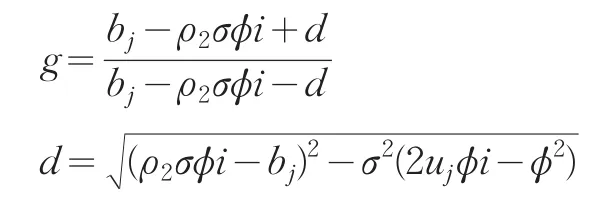
利用特征函数及其逆变换,可得
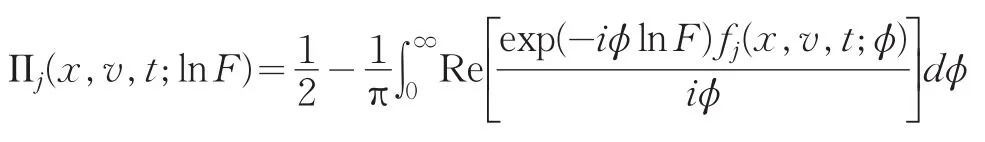
再利用Morten方法,可违约债券等价于债务的现值减去一个欧式看跌期权,从而可得债券定价公式为:
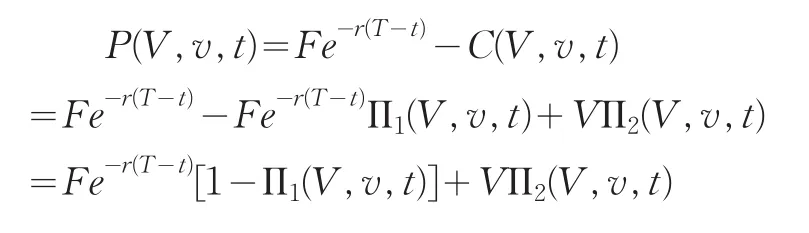
债券的违约概率:由上式可得
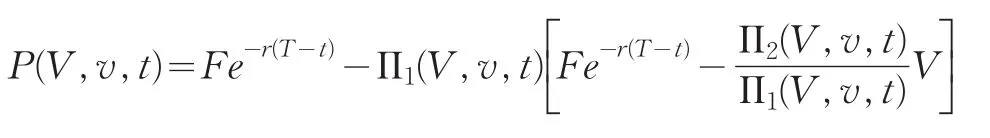
从而有[t,T]内的违约概率DP=Π1(V,v,t),挂号中的项表示违约预期贴现损失。
信用价差公式:此时债券的信用价差可表示为:
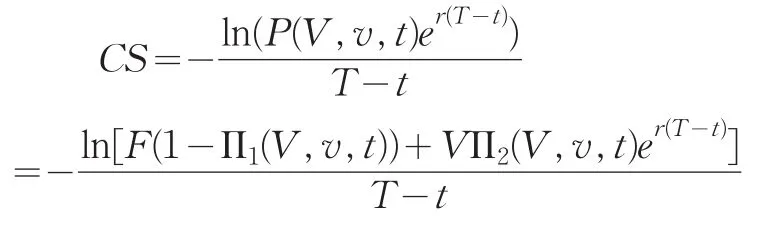
3 Black-Cox首次通过(first passage time)模型
(1)假设公式资产价格过程在风险中性下满足

波动率状态变量vt满足微分方程(2),且Cov(dW2,dW5)=ρ3dt
(2)公司发行了到期日为T的零息票债券,每份债券的面值为1。
(3)当公司资产触击到门槛值B时,就强制公司立即进入破产清算程序;当公司资产V大于门槛值B时,公司被认为有能力偿还债务并继续运营。
(4)发生违约时采用面值回收,为了简便起见,这里记常数R为回收率,P0(r,T),则面值回收具有形式RD,其中D为破产时刻零息票国债价格。
在这里假设无风险利率r和违约门槛值B都是常数,则在破产时刻t零息票国债价格D=exp[-r(T-t)],从而在破产时刻债券持有人可得Rexp[-r(T-t)]。此时债券价格满足方程
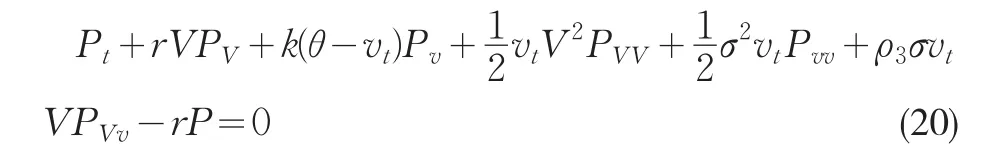
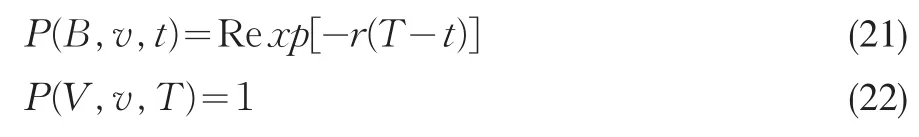
其中V0∈(B,+∞),且满足相应的边界和终值条件现在我们来求解方程(20),做变换W(x,v,t)=P(V,v,t)-Re-r(T-t),x=ln(V/B)。则方程变为:
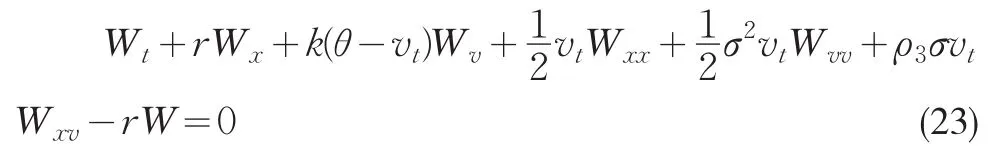
此时变量x的取值范围为x∈(0,+∞),相应的边界条件(21),(22)变为:

定义函数
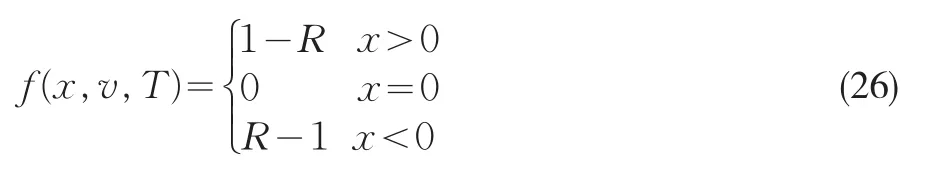
显然函数f(x,v,T)是一个奇函数,利用镜像法,则W(x,v,t)的奇延拓在空间Ω={x∈R,0≤t≤T}上满足柯西问题
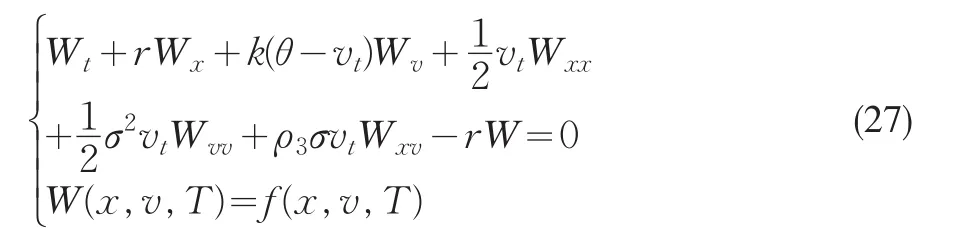
我们发现,可以把W(x,v,t)看作是到期日收益函数f(x,v,T)的欧式期权的价格,在风险中性测度下欧式期权的价格W(x,v,t)可以表示为:
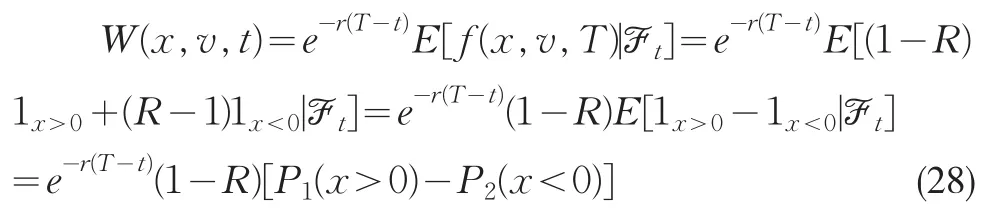
其中P1,P2分别表示风险中性下x>0和x<0的概率。把W(x,v,t)代入式(1.3.9)可得Pj(j=1,2)满足方程
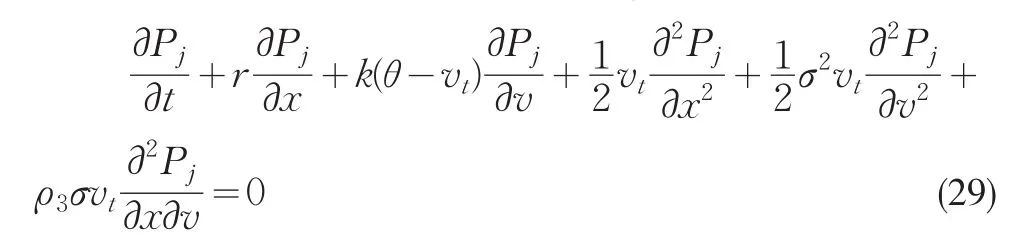
记 概 率 Pj(j=1,2)的 特 征 函 数 为 f(x,v,t;ϕ),则f(x,v,t;ϕ)也 满 足 方 程(29),终 值 条 件 为 f(x,v,T;ϕ)=exp(iϕx)。同理 f(x,v,t;ϕ)的解有如下形式为:

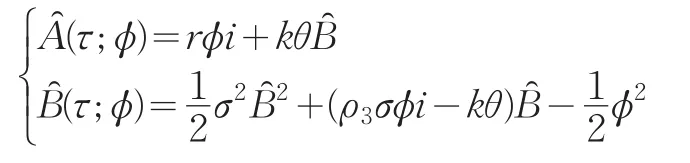
解上述方程有
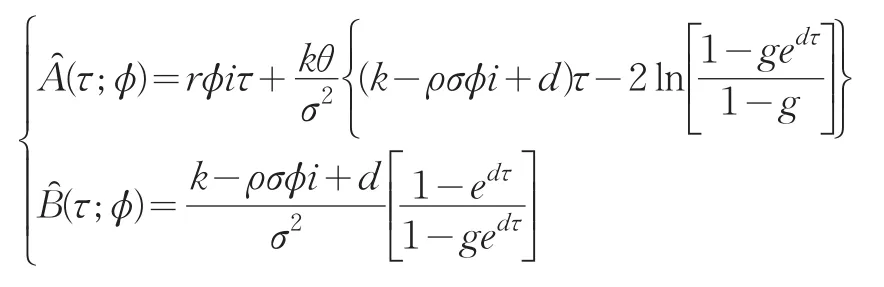
且
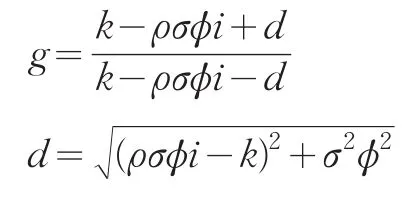
再通过逆变换可得
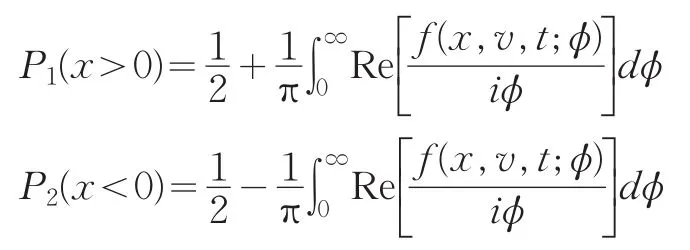
再通过变量回代,并把上式代入(28),从而可得风险中性下债券定价公式为:
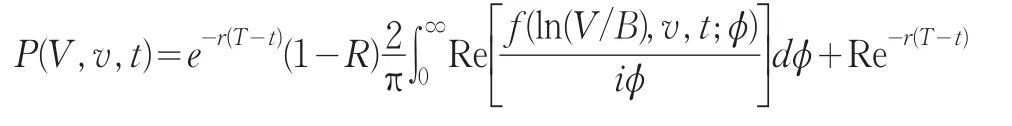
债券的违约概率:记公司在[t,T]内的违约概率为DF,在首次通过模型下,可违约债券价格可以表示为:

把上述债券价格公式代入可得债券的违约概率为

信用价差公式为:
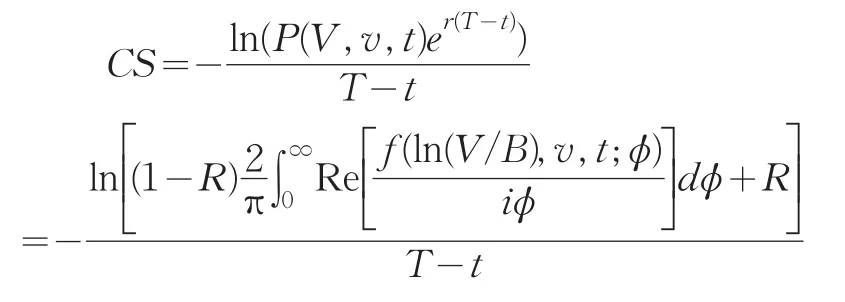
4 数值分析
在本节,我们将分析在随机波动率下信用价差的期限结构和波动率的波动率这个参数对信用价差期限结构的影响。取参数r=0.05,k=0.1,θ=0.2,ρ=ρ1=ρ2=0.5。图1、2分别演示了Merton模型下信用价差期限结构及其对波动率的波动率参数的依赖关系。由图1可以观察到,当准债务比K /V大于1时,则价差随期限递减;而当准债务比K/ V小于1时,价差随着期限先递增,随后又将下降,呈现明显的驼峰形状。这与常数波动率下Merton模型的信用价差期限结构完全相似。由图2可以看到,信用价差随着波动率的波动的增大而增大,这与我们的直觉也是一致的,因为波动率的波动越大表明风险越大,此时债券所要求获得的收益率也越大,价差也就随着增大。
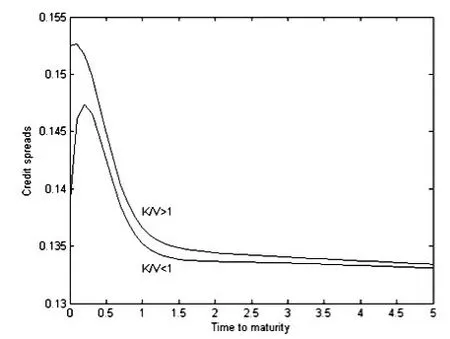
图1
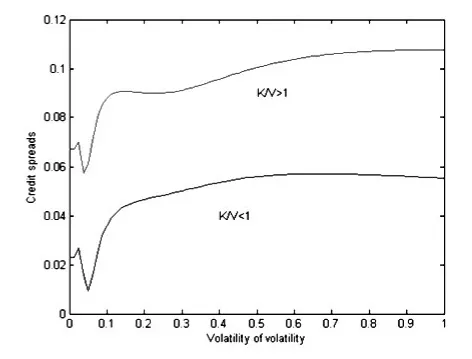
图2
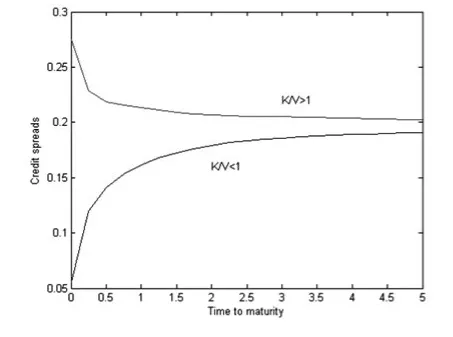
图3
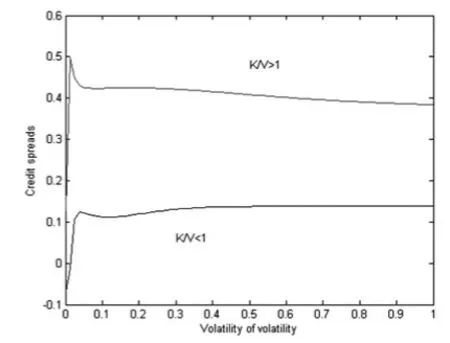
图4
图3、4演示了跳扩散模型下信用价差期限结构及其对波动率的波动率参数的依赖关系。由3可以观察到,当准债务比K/ V大于1时,则价差随期限递减;而当准债务比K/ V小于1时,价差是随着期限递增的。在图4中我们发现,在跳扩散模型中信用价差对波动率的波动并不敏感,特别是准债务比K/ V小于1时更是如此。这可能是由于在模型中本身就考虑到了跳量对价差的影响了,因此对波动率的变动反而不是很敏感了。
图5、6、7分别演示了首次通过模型下违约概率的期限结构和信用价差的期限结构及其对波动率的波动的依赖关系。由图5、6可以看到,违约概率和信用价差都是随着期限先增后减,呈现驼峰形状。图7则反映了价差随着波动率的波动的增大而增大,这与Merton模型下的情形相似,也与我们的直觉经验相符,即风险越大收益越大。由上述分析我们发现,随机波动率变量对Merton模型和首次通过模型还是有比较显著的影响,但是对跳扩散模型则影响并不显著。

图5
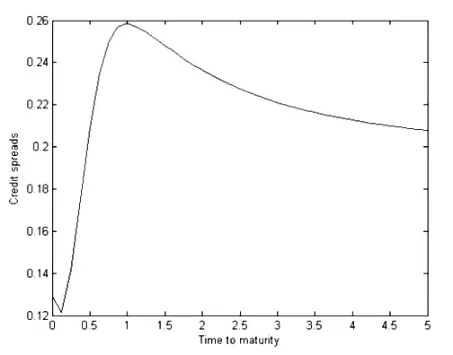
图6

图7
5 结束语
本文在假设状态变量波动率服从随机扩散过程下,分析了可违约债券的定价机制。通过特征函数及其逆变换的方法得到了可违约债券的价格及其信用价差的显式表达式。最后通过数值模拟发现随机波动率在Morten模型和首次时间通过模型中对信用利差有着显著的影响,而在跳扩散模型中则对信用利差的影响并不显著。
[1] Bates,D.S.Jumps and Stochastic Volatility:Exchange Rate Process⁃es Implicit in Deutsche Mark Options[J].Review of Financial Studies,1996,9(1).
[2] Heston,S.A Closed-form Solution for Options with Stochastic Volatil⁃ity with Applications to Bond and Currency Options[J].Review of Fi⁃nancial Studies,1993,6(2).
[3] Louis O.Scott.Pricing Stock Options in a Jump Diffusion Model with Stochastic Volatility and Interest Rates:Applications of Fourier Inver⁃sion Methods[J].Mathematical Finance,1997,7(4).
[4] Jean PF,Ronnie S,Knut S.Stochastic Volatility Effects on Default⁃able Bonds[J].Applied Mathematical Finance,2006,13(3).
[5] 陈侃,李时银.可违约债券在随机波动率假定下近似定价公式的求解[J].数学研究,2005,38(3).
[6] Chiarella,C.,Kwon,O.A Complete Markovian Stochastic Volatility Model in the HJM Framework[J].Asia Pacific Financial Markets,2000,7(4).
[7] Duffie,Darrell,Ken Singleton.Modeling Term Structures of Default⁃able Bonds[J].Review of Financial Studies,1999,12(4).
[8] Hobson,G.,Rogers,L.Complete Models with Stochastic Volatility[J].Mathematical Finance,1998,8(1).
[9] Sabanis S.Stochastic Volatility[J].International Journal of Theoretical and Applied Finance,2002,5(5).
[10] 王春峰,蒋祥林,吴晓霖.随机波动性模型的比较分析[J].系统工程学报,2005,20(2).
[11] 闫海峰,刘利敏,杨建奇.随机波动率模型的效用无差别定价和套期保值策略[J].系统工程学报,2007,22(4).

