三参数Burr分布经验贝叶斯估计的渐近性

刘荣玄，朱先阳，安 萍

0 引言

BurrI.W.在1942年基于微分方程F(x)/dx=dF(x)(1 -F(x ))g(x , F(x ))引入了Burr分布函数,这一分布在精算学、质量控制和可靠性研究中有着广泛的应用。因此许多学者致力于Burr分布的研究。文献[1]讨论了BurrTypeXII分布的统计推断,文献[2]讨论了两参数BurrXII分布的经验Bayes检验问题,文献[3]讨论了Burr-XII。

部件可靠性指标的贝叶斯估计,文献[4]讨论了熵损失函数下Burr分布参数的Bayes估计。文献[5]讨论了指数族刻度参数EB估计的渐近最优性。关于三参数BurrI分布中形状参数EB估计的研究,目前尚未有文献发表.本文将在平方损失下研究其EB估计,并讨论其收敛速度。

假设在θ已知的条件下,三参数BurrI分布为：

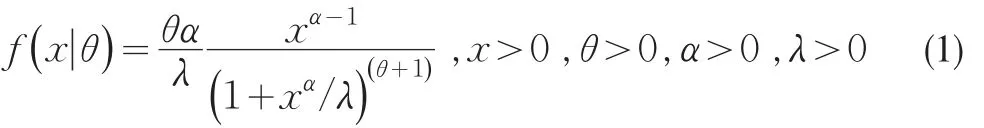
其中，参数α,λ已知,λ为刻度参数,θ为形状参数,α为不等式参数。由于三参数BurrI分布是一类重要的寿命分布,随机变量X的取值x总是正的,因此不妨假设x≥ε,ε为给定的任意小的正实数。

在Bayes统计中,参数θ为随机变量,假设它的先验分布为H()θ,属于先验分布族F={H()θ: θ＞0, E()θδ＜∞ ,δ＞2,},则随机变量(r.v.)X的边缘分布为：

r.ν.θ的后验分布为：

π(θ|x)∝f(x|θ)H′(θ)

取损失函数为平方损失,即

其中d为参数θ的仅与x有关的判决函数,显然它是对称损失函数。

于是可得参数θ的Bayes估计为：

其相应的Bayes风险为

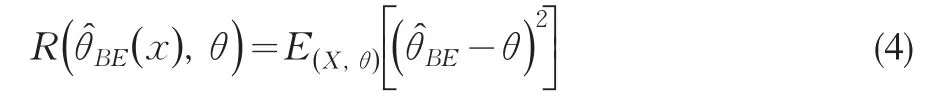
这里的E(X,θ)表示对(X , θ)的联合分布取期望.

引理1对于三参数BurrI分布(1),在均方损失函数(3)下，其形状参数θ的Bayes估计为：

其中：

f′X(x)是fX(x)的导数。

证明：由(1.2)式可得

解得

将（6）式代入（4）式得

证毕。

将(5)式代入(4)式得

1 EB估计的构造

假设随机向量序列(X1, θ1),(X2, θ2), …, (Xn, θn) 与(X , θ)相互独立且有相同的分布(iid),X1, X2, …, Xn,为iid的随机变量序列,它们是可观测的,与X独立且有相同的边缘概率密度fX(x),X1, X2, …, Xn为历史样本,X为当前样本,θ1, θ2, …, θn和θ为不可观测的,但有相同的先验分布H(θ)，并假设：

（1）fX()x ∈Cs,M, x∈R1,其中s＞2为正整数,Cs,M表示R1中的一族概率密度函数,其s阶导数存在,连续且绝对值不超过M。

（2）Ki(x)(i=0, 1)为Borel可测实值核函数,满足

①Ki(x)=0,x∉(0, 1);

②Ki(x)为有界的,除有限点集外是可微的,且微分有界;

定义fX(x),f′X(x)的核估计分别为：

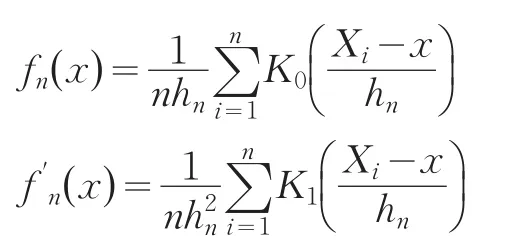
其中，hn＞0,当n→∞时, hn→0, nhn→∞。

ϕn(x)实数

这里的E∗表示对随机向量(X1, X2, …, Xn, (X , θ))的联合分布求数学期望。

这样构造的θ的EB估计与其Bayes估计所产生的效果相当,即在一定的条件下当历史记录较多时,EB估计所产生的风险近似于Bayes估计所产生的风险,结论是:

定理1在平方损失下，如果上述A、B条件成立，且满足EX(| X|6s)＜ ∞,E(|θ |δ)＜ ∞,对 给 定的 正数s＞2,δ＞2，时,则有c为常数。

2 定理1的证明

在证明定理的过程中需要用到下列几个引理,并假设c为常数,且在同一等式或不同等式中可以代表不同的常数。

引理2在平方损失下,有

这里的EX表示对随机变量X取数学期望,En表示对随机向量(X1, X2, …, Xn)的联合分布取数学期望。

证明：见文献[6]中的引理3。

引理3设Y, Y′分别为r.v,y, y′为实数,L＞0,则对0＜γ＜2有

证明：见文献[7]中的引理3.1。

引理4X1, X2, …, Xn,…,为iid的随机变量序列,满足上述条件A、B,当hn=n-1/(1+2s),0＜γ＜2时,则有

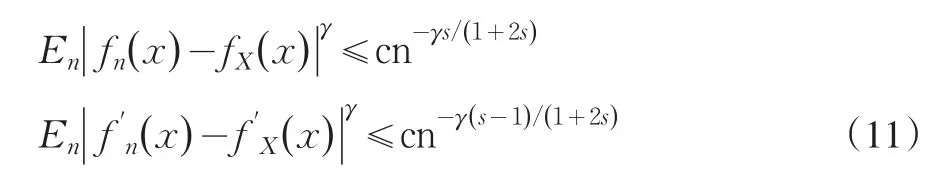
证明：见文献[9]中的引理3。

引理5若1/2＜γ＜1-1/(2s),EX(X6s)＜∞,s＞2为整数,则有

证明：因为

根据 HÖlder不等式有

从而

又因为

而

由（13）、（14）式可知（12）式成立。

引理6对于给定的自然数δ,δ ＞2,当E(|θ |δ)＜ ∞,时,则有

由(16)、（17）式可知（15）式成立。

定理1的证明：

证明

令

由引理2有

在X已知的条件下，由引理3和引理4有

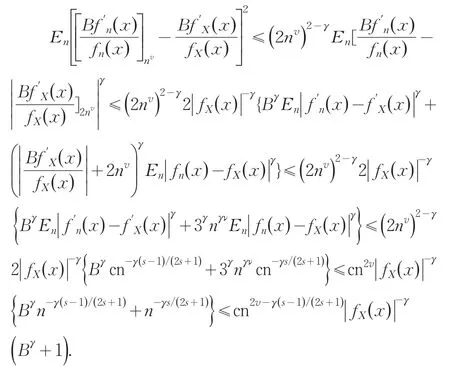
由引理5可知

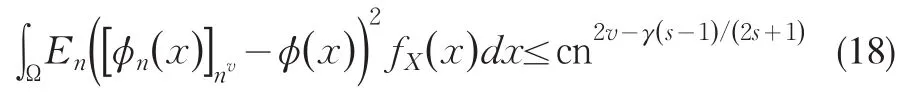
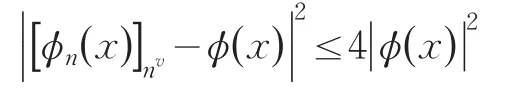
由HÖlder不等式和Markov不等式，对于任意给定的δ，δ＞2，有

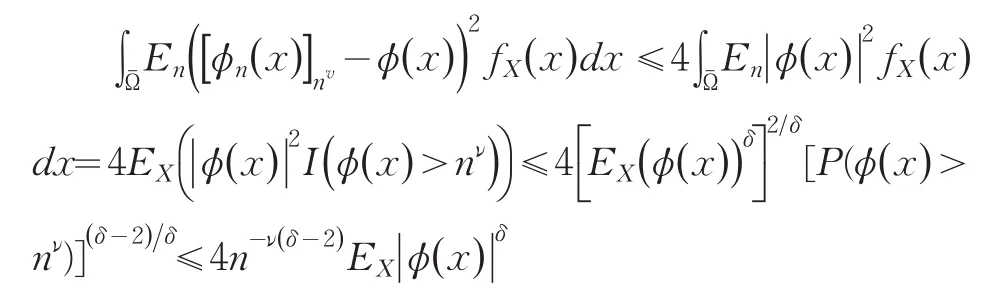
由引理6知

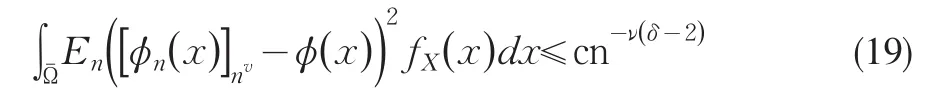
在(18)和(19)式中取ν=γ(s -1)/δ(1 +2s),则有

证毕。

3 例子

下面的例子说明存在满足定理条件的先验分布。

设r.vX的条件概率密度为(2)式,取θ的先验分布为其共轭分布Γ(r, ρ) ,即

于是可得r.vX的边缘分布为：

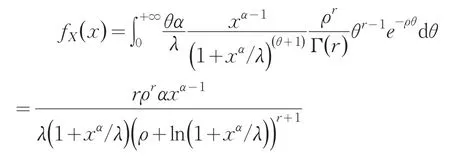
显然fX(x)满足上述A,B中的条件。

由文献[10]可知给定自然数δ,δ＞2,则有

当r较大时有

由此可知定理1中的条件全满足,则定理1的结论成立。

[1] 王炳兴.Burr TypeXII分布的统计推断[J].数学物理学报,2008,28A(6).

[2] 韦程东,陈志强等.两参数BurrXII分布的经验Bayes检验问题[J].工程数学学报,2010,27(2).

[3] 王婷婷等.Burr-XII部件可靠性指标的贝叶斯估计[J].系统工程,2009,27(5).

[4] 陈志强,韦程东等.熵损失函数下Burr分布参数的Bayes估计[J].广西师范学院学报(自然科学版),2007,24(3).

[5] 刘荣玄.指数族刻度参数EB估计的渐近最优性[J].数理统计与管理,2010,29(6).

[6] 韦来生.连续型多参数指数族参数的渐近最优的经验Bayes估计[J].应用概率统计,1985,1(2).

[7] 赵林城.一类离散分布参数的经验贝叶斯估计的收敛速度[J].中国数学研究与评论,1981,(1).

[8] 刘次华,李少玉.线性指数模型参数的经验贝叶斯估计[J].华中科技大学学报,2006,34(3).

[9] 田霆,刘次华.定数截尾场合下Weibull分布的形状参数置信上下限[J].南昌大学学报(理科版)2010,34(3).