连续梁桥上不同连接形式的无砟道岔群受力与变形分析
郝远行,李培刚,杨荣山
(西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031)
道岔在使用过程中,通常会与其他道岔一起形成道岔群,若将道岔群放在连续梁桥上,则钢轨受力与变形将会相互影响[1]。道岔群的连接形式多种多样,且不同的连接形式对道岔群的受力与变形影响各不相同,其变化规律将更为复杂。本文通过建立岔—桥—墩一体化有限元模型,分析了在不同连接形式下的无砟道岔群在连续梁桥上的受力与变形特点,并提出了针对性的建议。
1 计算模型及参数
1.1 计算模型
桥上无砟轨道岔—桥—墩空间一体化模型如图1所示。其中,钢轨、道岔板、支承层和桥梁用空间梁单元模拟[2-4]。岔枕和扣件作为一个整体,道岔板和支承层之间的纵横向凸台以及支承层和桥梁之间的滑动摩擦层都用非线性弹簧单元来模拟。该非线性弹簧单元采用理想的弹塑性本构关系,极限滑动阻力对应点位移为0.5 mm[5-6]。考虑到边界条件对计算结构的影响,两端路基上无砟轨道长度取为100 m,两端固结。将上述桥上(桥跨布置如图2)无砟轨道空间模型采用有限元法计算,并用计算机语言编制成通用程序,以满足不同情况下的快速计算。
1.2 计算参数
以2组采用60 kg/m钢轨及不同连接形式的18号可动心轨无砟道岔布置在6×32 m连续梁桥为例,桥跨布置如图2所示。为消除边界影响,在连续梁两端分别各布置3跨32 m简支梁。每组道岔全长69 m,均布置在连续梁上,辙跟类型为限位器。由于轨下基础为无砟,所以岔枕与混凝土道床视为刚性联结,计算中岔区道床纵向阻力类型为常阻力型,其值取极大值1 000 kN/m。系统温度变化按升温考虑,道岔温度变化幅度取 50℃,桥梁取 20℃,道岔板取 35℃[2]。

图1 桥上无砟道岔空间模型纵断面
2 计算结果比较与分析
2.1 计算工况
考虑采用如图3所示的5种道岔连接形式作为计算工况。

图2 桥跨布置

图3 道岔群连接形式
2.2 基本轨附加温度力比较
各种形式的道岔连接方式对最大基本轨附加温度力的影响比较如表1所示。基本轨附加力如图4和图5所示。图中坐标原点为左桥台位置,横坐标x表示钢轨单元距左桥台距离。基本轨附加力为正表示力为压力,为负表示力为拉力。

图4 不同连接形式下道岔基本轨附加力P
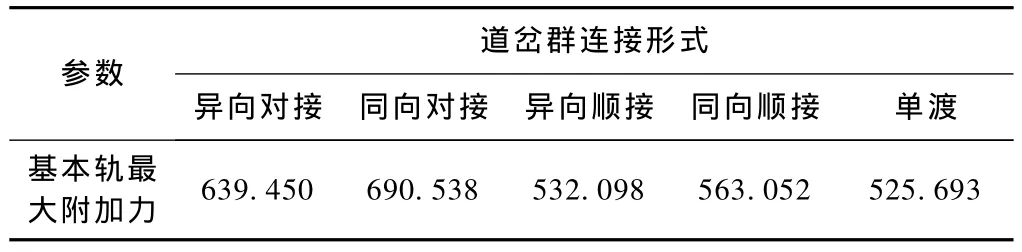
表1 不同形式的道岔连接方式对基本轨附加温度力的影响比较 kN
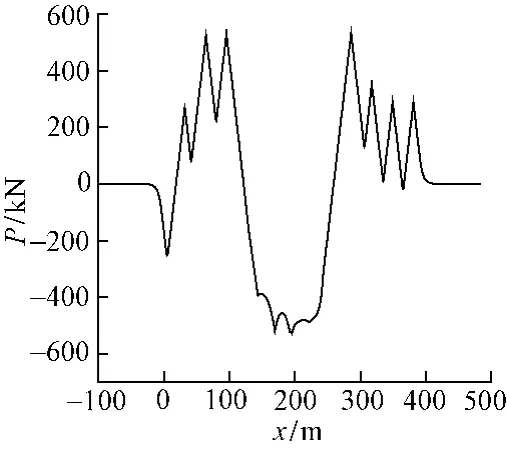
图5 单渡道岔基本轨附加力
由图4可以看出,对接的两种道岔连接形式的基本轨附加力图相似,最大附加力均出现在距离左桥台191 m处,而顺接的两种道岔连接方式的基本轨附加力不同,异向形式的最大附加力出现在距离左桥台287 m处,同向的则出现在200 m处。
从表1可以看出,在各种连接形式中,顺接方式比对接方式的道岔基本轨所受附加力要大,同种连接方式中,同向的要比异向的更大,而单渡形式的道岔基本轨所受附加力是所有形式当中最小的。因此,在道岔基本轨维护中,应对同向或者对接形式的道岔加以足够的重视。
2.3 钢轨伸缩位移比较
各种形式的道岔连接方式对钢轨伸缩位移的影响比较如表2所示。
从表2中可以看出,单渡道岔形式的直尖轨尖端相对于岔枕位移为最大,最大值出现在2号道岔。顺接方式道岔的直尖轨尖端相对于岔枕位移比对接方式的更大。在同种连接方式中,异向和同向的尖轨相对位移相差很小。
对于心轨尖端相对于岔枕的位移,单渡形式的道岔为所有形式中最小。顺接方式比对接方式的相对位移更大,而在对接方式中,异向和同向的相对位移相差很小。在顺接方式中,异向形式道岔的心轨尖端最大相对位移比同向形式的更大。
总的来说,在各种连接形式中,直尖轨尖端和心轨尖端相对于岔枕位移相差均不大,在合理的桥跨布置中均能满足设计要求。
2.4 限位器及间隔铁受力比较
各种形式的道岔连接方式中限位器及间隔铁作用力比较如表3所示。
从表3可以看出,单渡形式道岔的限位器不受力。顺接方式只有一组道岔的限位器受力,且比对接方式的受力更小,在这种连接方式中,异向的最大受力比同向的更大。对接方式两组道岔的限位器均受力,且同向的最大受力比异向的更大。

表2 不同形式的道岔连接方式对钢轨伸缩位移的影响比较 mm

表3 不同形式的道岔连接方式对限位器及间隔铁作用力比较 kN
单渡形式道岔的间隔铁最大受力为所有形式中最小。顺接方式比对接方式的最大受力更大。在同种连接方式中,异向的间隔铁最大受力比同向的更大。
在对接方式中,限位器受力比较不利,可适当增加限位器的数量,以保证限位器满足受力要求。顺接方式的间隔铁受力较大,但和对接方式的道岔相差不大。单渡形式的道岔传力部件受力最小,可尽量减少传力部件的使用,以达到使用的经济最优化。
3 结论及建议
1)以对接方式连接的道岔基本轨所受最大附加力比顺接方式更大,单渡形式的道岔基本轨所受最大附加力最小,同种连接方式中,同向的比异向的受力更大。因此,在道岔基本轨维护中,应对同向或对接形式的道岔加以足够的重视。
2)在各种连接形式中,直尖轨尖端和心轨尖端相对于岔枕位移相差不大,在合理的桥跨布置中均能满足设计要求。
3)在对接方式中,限位器受力比较不利,可适当增加限位器的数量或加强限位器结构,以保证限位器满足受力要求。顺接方式的间隔铁受力较大,但和对接方式的间隔铁受力相差不大。单渡形式的道岔传力部件受力最小,可尽量减少传力部件的使用,以达到使用的经济最优化。
[1] 王平,刘学毅.无缝道岔计算理论与设计方法[M].成都:西南交通大学出版社,2007.
[2] 李成辉.轨道[M].成都:西南交通大学出版社,2005.
[3] 杨荣山,刘学毅,王平.简支梁桥上无缝道岔纵向力影响因素分析[J].西南交通大学学报,2008(5):666-672.
[4] 王平.无缝道岔群对钢轨位移和纵向力的影响研究[J].铁道学报,2002,24(2):74-78.
[5] 西南交通大学.跨区间无缝线路无缝道岔设计方法的优化研究报告[R].成都:西南交通大学,2003.
[6] 刘哲,王平.连续梁桥上典型道岔群纵向受力与变形分析[J].铁道建筑,2011(7):124-127.

