两大部类产品价值构成的拉格朗日乘数法之解

陶为群

（中国人民银行 南京分行,南京 210004）

0 引言

马克思的社会扩大再生产理论对我国的国民经济运行具有重大现实指导意义。两大部类产品的价值构成,即生产资料与消费资料部类产品的价值构成,是再生产实现过程中非常重要的参数。科学地获取这些参数值，是将马克思的再生产理论应用于现实的前提条件。由于两大部类是理论化分类而非现实统计，所以只能根据投入产出表推算两大部类产品的价值构成等参数。陶为群曾提指出，《投入产出分析》教材和工具书所介绍的推算产品价值构成的单一方法，可以归结到UV表方法框架中，并且提出了在UV表框架下按产品工艺假定的另一种推算方法，用非线性规划得出新方法的推算结果，但未能给出此新方法下价值构成参数的显性算式。陶为群、陶川（2010）给出了按此新方法的两大部类产品价值构成的极大似然估计显性算式和实际算例。但是，他们在推算过程中没有考虑到马克思社会再生产原理指出的两部类间产品交换关系，因而所获结果还有待加以改进。

1 一种在UV表方法框架中推算两大部类价值构成的新方法和算式

UV表方法是编制投入产出表时普遍使用的一种间接推导法。设国民经济中有n个部门，每个部门都生产多种产品，它们共生产k种产品。在统计时，只能获得每个部门对k种产品的消耗投入和产出数据，也就是获得产品×部门表U表，和部门×产品表V表。要通过U表和V表推导出按部门或按产品的投入产出表，也就是部门×部门或产品×产品投入产出表。马克思的再生产理论把具体的多种产品按基本用途分为生产资料和消费资料两类，即第Ⅰ、第Ⅱ部类，两大部类产品的价值构成类似于概括的两类产品投入产出表。两类产品都是由国民经济中n个生产部门所生产，也可以看做是由k种产品部门所生产。因而，可以通过统计获得的n个生产部门或k种产品部门的价值构成表，以及生产部门或产品部门的两类产品产出数据，推导出两大部类产品的价值构成。更确切地说，是运用价值构成×生产部门表或价值构成×产品部门表（U表），以及生产部门×两类产品表或产品部门×两类产品表（V表），按照某种假定条件，推导出价值构成×两类产品表。所以，推算两大部类产品的价值构成，实质上是将一般的UV表方法，运用到马克思的社会再生产理论的一些具体内容，获得具体的理论结果。

记国民经济中第j生产（或产品）部门的总产出（或总产品）是Uj（j=1，2，…,n或j=1，2，…,k）；uc j，uv j，um j分别是该部门生产中的生产资料消耗、工资支出、剩余价值，也就是该部门的价值构成。pjΙ，pjΙΙ分别是该部门生产出的第Ⅰ、第Ⅱ部类产品。国民经济各部门生产出的第Ⅰ、第Ⅱ部类产品分别是XΙ，XΙΙ；Cl，Vl，Ml分别是第l部类（l=Ι,ΙΙ）的生产资料消耗、工资支出、剩余价值，也就是该部类产品的价值构成。现在要运用统计获得的国民经济各部门的价值构成，以及它们的第Ⅰ、第Ⅱ部类产品产出数据，推算出两大部类产品的价值构成。由于马克思的再生产模型中生产资料消耗包含了固定资产折旧消耗，因而推算时需要把j部门的固定资产折旧纳入到uc j之中。

当遵照产品工艺假定，运用n个生产部门的价值构成表，以及它们的两类产品产出数据，推算两大部类产品的价值构成，算式如下：

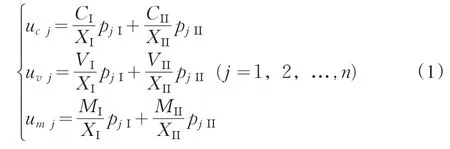
2 推算两大部类产品价值构成应当遵从的两部类产品交换约束条件

马克思的再生产模型中设不变资本的周转周期为1年，这相当于把固定资产折旧计入到生产资料消耗里。对前面已经确定了含义的字母前面加符号Δ表示增量。因为第Ⅰ部类的总产品（CΙ+VΙ+MΙ）实物形态是生产资料，扣除补偿本部类和第Ⅱ部类的生产资料消耗CΙ和CΙΙ，剩余的（VΙ+MΙ-CΙΙ）都必然用于本部类和第Ⅱ部类新增生产资料ΔCΙ和 ΔCΙΙ。因此就存在关系式：

马克思在《资本论》中已经指出，这种补偿和新增使用，是经过部类内部以及两个部类之间的产品交换（交易）完成。马克思还特别指出：第Ⅰ部类的总产品当中的工资支出和剩余价值中用于企业主消费和新增工人工资部分，要转化为消费资料；第Ⅱ部类的总产品当中的生产资料消耗和新增生产资料部分，要转化为生产资料；这两个转化通过相互等价交换实现。而（2）式所表达的，是与马克思特别指出的两个部类之间相互等价交换同样的含义。

在核算统计上，投资是国内生产总值当中没有被消费掉的部分，由于马克思的再生产模型中，固定资产折旧计入到生产资料消耗里，当年新创造价值（VΙ+MΙ）+（VΙΙ+MΙΙ）对应于统计上的国内生产净值；新增生产资料ΔCΙ+ΔCΙΙ是净投资，对应于统计上的资本形成净额。而在推算两大部类产品的价值构成时，投入产出表当中的资本形成净额是一个已知数，用IN表示，由（2）式，就得出推算两大部类产品的价值构成时的一个约束条件：

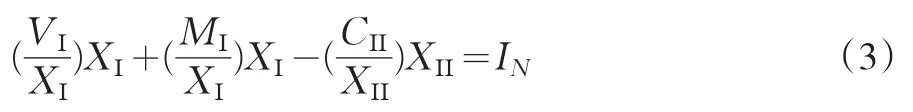
根据投入产出表推算两大部类产品的价值构成，应当满足由于两部类产品交换而产生的这个约束条件，理论上才符合马克思的社会再生产原理。

3 两大部类产品价值构成的拉格朗日乘数法之解

下面遵照产品工艺假定，按照(1)式推算两大部类产品的价值构成，并且满足约束条件(3)式。按照(1)式推算两大部类产品的价值构成，还应该与统计到的社会总产品价值构成一致，与统计到的第Ⅰ、第Ⅱ部类产品总量一致。即还满足约束条件：

在产品工艺假定下推算两大部类产品的价值构成，就是对(1)、（3）和(4)式共同构成的方程组，求解其中的6个价值构成参数变量。方程组有3n个方程、5个约束条件，方程个数加上约束条件个数超过了待解变量数，因而只能有最小二乘解。所以，记（1）式各方程左右两边的离差平方和为Z。则：

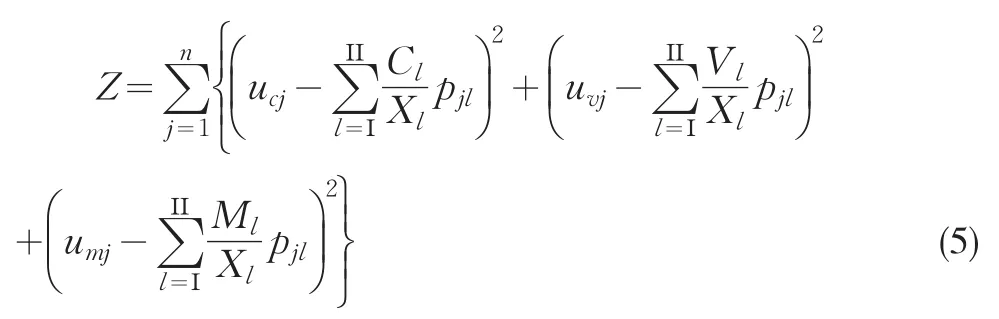
应当在约束条件(3)和(4)式下使离差平方和Z取得最小值，就是一个解条件极值问题。运用拉格朗日乘数法，构造拉格朗日函数Q：

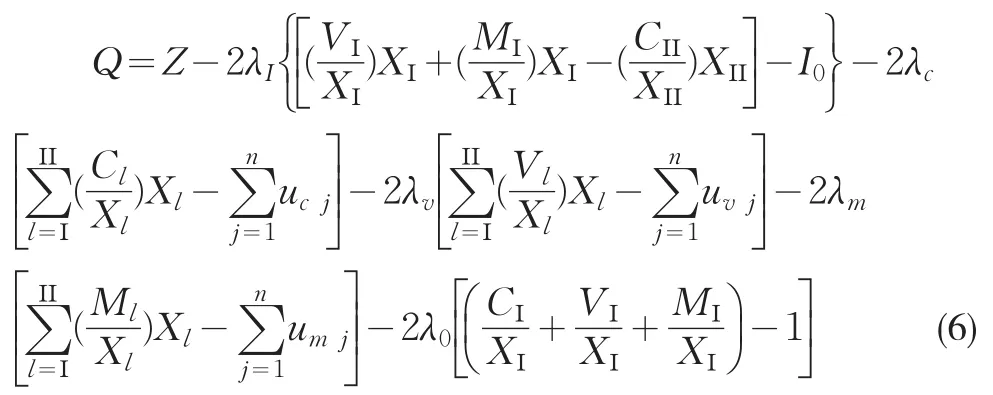
现在以矩阵形式表示，记

那么，约束条件（3）和（4）式在一起可以表示成矩阵关系式

将拉格朗日函数Q依次对参数求偏导数，并令偏导数等于0，依次得到6个方程，合在一起可以表示成矩阵关系式：

只要各部门产出矩阵P的两列不成倍数关系，由上式就可以得出:

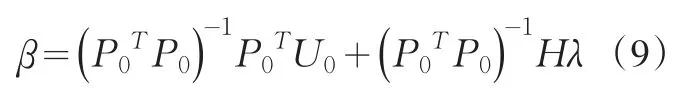
带入（7）式得:

由此解出拉格朗日乘数列向量：

带入（9）式，就获得参数列向量β的计算值：

由于分块对角矩阵的逆矩阵也是分块对角矩阵，所以上式中的计算并不复杂。式中:

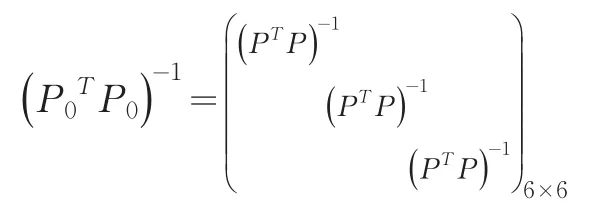
式（11）中的各个分量，就是在满足两部类产品交换约束条件下，推导出的显性的两大部类产品价值构成的拉格朗日乘数法之解。对此，可以使用Excel工具方便地解出具体数值。

4 实际算例及结果分析

下面使用《全国投入产出表1981（试编）》中有关数据,计算出两大部类产品价值构成的拉格朗日乘数法之解。选用该表数据的原因是,表中明确列出了各部门产出当中的生产资料pjΙ和消费资料pjΙΙ数据，能够避免用不考虑进出口的数据粗略确定pjΙ和pjΙΙ而导致的推算偏差。表1上部的数据，是该投入产出表中统计的国民经济各部门的投入价值构成和产出生产资料与消费资料数据；表1下部是用以上数据按照本文的拉格朗日乘数法之解，推算的两大部类产品价值构成。其中，当年最终产品合计是4351.66亿元，消费合计是2781.46亿元，固定资产折旧合计是411.46亿元，所以资本形成净额即（3）式中的IN应当是最终产品减去消费和固定资产折旧，为1158.8亿元。经验证，拉格朗日乘数法之解满足约束条件(7)式。

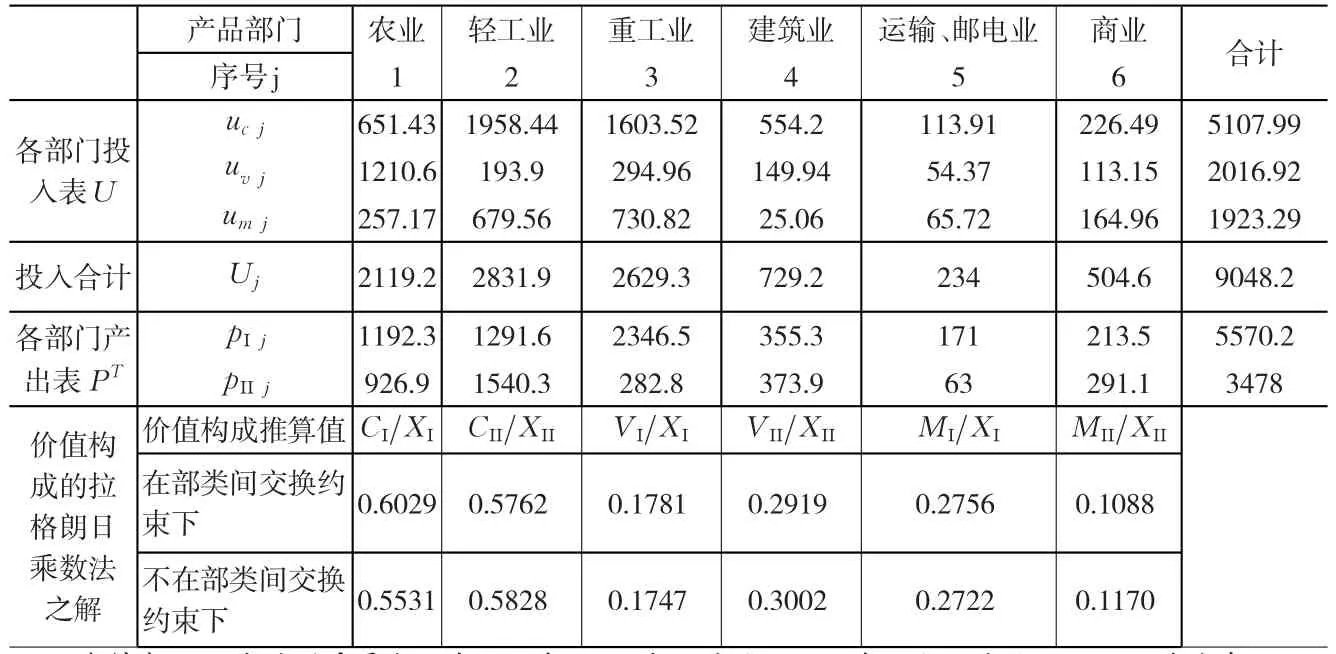
表1 1981年全国各部门产品价值构成与两大部类产品价值构成的拉格朗日乘数法之解

为了观察两个部类之间的产品交换约束条件对于推算结果的作用，现在对表1最后两行的差别，做点简要的比较分析。在部类间交换约束条件（3）式和约束条件（4）式下，生产资料的有机构成是(CΙ/XΙ):(VΙ/XΙ)=3.3852:1；消费资料的有机构成是 (CΙΙ/XΙΙ):(VΙΙ/XΙΙ)=0.5762:0.2919=1.9740:1；生产资料的有机构成显著高于消费资料,符合经济学原理和人们的一般感性认识。这是因为生产资料生产的资金与技术明显比消费资料生产密集。如果未遵从部类间交换约束条件，也就是丢掉部类间交换约束（3）式而仅使用约束条件（4）式，同样应用拉格朗日乘数法，求解出的生产资料的有机构成就变为0.5531:0.1747=3.17:1，而消费资料的有机构成就变为 0.5828:0.3002=1.94:1，生产资料与消费资料的有机构成差异性降低。这说明，马克思社会再生产原理指出的两部类间产品交换关系，对于推算两大部类产品的价值构成在理论上是必要的，在数据结果上也确实有改进作用。

[1]陶为群,陶川.两大部类产品价值构成的约束极大似然估计[J].西安财经学院学报，2010,(4).

[2]姚天行等.大学数学[M].北京:科学出版社,2002.

[3]因特里格特等.经济计量模型、技术与应用[M].北京:中国社会科学出版社,2004.