一种弹簧摆运动规律的研究
姜付锦
(武汉市黄陂区第一中学,湖北 武汉 430030)
题目.如图1所示,A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳与轻弹簧均处于水平,弹簧处于自然状态.将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上,则(A)两球到达各自悬点的正下方时,两球动能相等.(B)两球到达各自悬点的正下方时,A球动能较大.(C)两球到达各自悬点的正下方时,B球动能较大.(D)两球到达各自悬点的正下方时,A球受到向上的拉力较大.
解析:根据机械能守恒定律,A球在下降的过程中,重力势能全部转化为小球的动能;B球在下降的过程中,重力势能转化为小球的动能和弹簧的弹性势能,所以A球的动能较大,故(B)选项对;但对于(D)选项的分析不能简单地认为此时的弹簧的长度就是小球曲线运动的曲率半径.参考文献[1]一文中分析结果是:由功能关系计算B球在最低点的速度大小,但速度的方向以及曲率半径的确定仍难度很大,要涉及B球运动过程的细节,需通过微分方程才能求解.笔者通过MathCAD对这个问题进行了分析并得到原题中的正确答案,以下是分析过程,文中若有不当之处请各位物理同仁批评指正.
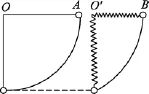
图1
1 建立模型

图2
以振子的悬点为坐标原点建立如图2所示的坐标系xOy,开始时弹簧振子处于水平放置,弹簧处于原长L0状态,设弹簧的劲度系数为k,振子的质量为m,把弹簧振子由静止释放,在某一时刻,弹簧振子的坐标为P(x,y).
1.1 微分动力学方程
由受力分析可以得弹簧摆在水平与竖直两个方向上的合外力.在水平方向上有

在竖直方向上有

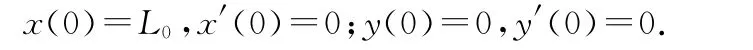
整理后得,在水平方向上有

在竖直方向上有

1.2 用 MathCAD制图
为了研究方便,设L0=20m,g=10m/s2,k=1N/m,m=1kg,用MathCAD制图如图3所示.


图3
1.3 图形分析
(1)轨迹图.
图3(a)是弹簧摆的运动轨迹,由图可知其轨迹不是一个圆周,弹簧的长度先变长后变短.在最低点小球的速度方向是水平的,此时小球到悬点的距离为47.7m.
(2)弹簧长度图.
弹簧的长度随时间是周期性变化,周期为8.325s,由图3(b)可知在一个周期内先变大后变小且在最低点时长度约为47.7m(最长),由胡克定律可求得在最低点时弹簧的弹力为27.7N<30N.
(3)小球水平速度随时间变化图.
如图3(c)所示,小球的水平速度随时间是周期性变化的,周期为16.875s,最大水平速度为13.298m/s.
(4)小球竖直速度随时间变化图.
如图3(d)所示,小球的竖直速度随时间是周期性变化的,周期为8.325s,在一个周期内先正向变大再减小,然后反向变大最后减小,最大竖直速度为19.186m/s.
(5)小球合速度随时间变化图.

图4
如图4所示,小球的合速度大小随时间变化的周期为8.325s,在一个周期内先变大再减小,然后变大最后减小,且在最低点的速度约为13.41m/s,最大速度为19.88m/s.
(6)轨迹曲率半径随时间变化图.

图5
小球运动轨迹的曲率半径随时间是周期性变化,周期为8.325s.由图5可知在一个周期内曲率半径先变大再减小,然后变大最后减小,在最低点时的曲率半径约为10.06m,比弹簧的原长小,既不是弹簧的原长也不是弹簧此时的实际长度.
(7)小球的能量随时间变化图.

图6
图6中 Eki、Ep1i、Ep2i、Ei分别为小球在下落过程中,动能、重力势能(设原点的重力势能为0)、弹性势能和机械能.由图可知它们变化的周期为8.325s,小球在下落的过程中机械能是守恒的(总能量为0).
1.4 与单摆运动规律的比较
若题中A球的轻绳长为47.7m,由机械能守恒定律可求得单摆在最低点时的速度是,取L=47.7m,得v=30.89m/s;绳子的拉力为,得F=30N,都比弹簧摆在最低时的大,所以原题中(B)、(D)为正确答案.
2 结语
文中的弹簧摆在最低点时速度方向是水平的,是由弹簧摆的初始值所决定的,即开始时弹簧处于原长且振子没有初速度.若弹簧不是原长或振子有初速度,则弹簧摆的轨迹和运动规律将很复杂的[2][3],这里暂不讨论.以上的分析只是弹簧摆运动规律的一种特殊情况,这是符合原题目中情景的,故答案为(B)、(D).
1 黄雄.例说力学的瞬时规律和过程规律.物理通报,2011(5):38-40
2 杨正波,夏清华,刘思平.不同控制参数上的弹簧摆.大学物理,2011,5(30):23-26
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论

