谈谈几种非常见物理图像的应用

王金聚

（浙江省温州中学，浙江 温州 325000）

图像具有直观、形象、简明的特点，它能直观地描述物理过程、形象地表达物理规律、简洁地阐明各量之间的相互关系，是分析、研究问题常用的方法之一.运动学中的v－t、x－t图像、电学中的U－I、i－t、u－t图像、磁学中的B－t、Φ－t图像、热学中的P－V、V－T、P－T 图像等，都是我们在平时解题中经常使用的图像，但也有一些图像虽不太常用，但用起来却往往能“手到病除”、立竿见影，起到计算法所不能及的效果.现举例如下：

1 v－t图像，即速率时间图像

对追及、相遇问题，有时涉及多个物体、多次相遇，物理过程多、情景复杂，难以在头脑中建构清晰的运动图景.这时候，恰当地利用图像，就能直观地展示复杂物理情景，建构清晰的运动过程，帮助我们找到解题的切入点.

例1.每颗子弹从枪口射出的速度大小都是30m／s，某人每隔1s竖直向上开一枪，假定子弹在升降过程中都不相碰，不计空气阻力，试求：

（1）空中最多能有几颗子弹？

（2）设t＝0时将第一颗子弹射出，在什么时刻它和后面的子弹在空中相遇？

（3）每颗子弹分别能与几颗子弹在空中相遇？

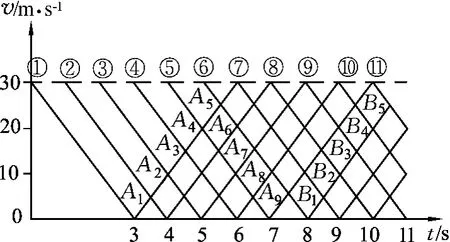
图1

解析：以v表示速率，设子弹射出后经t秒钟到达最高点，由v0＝gt可得t＝3s，作出子弹在空中运动的速率－时间图像，如图1所示，图中图线① 、② 、③ …分别表示第1颗、第2颗、第3颗…子弹的速率－时间图像.显然，任意两条图像的交点都表示两子弹速率相同且一升一降时的情况，交点的横坐标表示相遇的时刻，交点的纵坐标表示相遇时的速率大小.

由图可知，当第7颗子弹即将射出时，第1颗子弹即将落地，所以说空中最多有6颗子弹.由于升、降图线的斜率大小都表示重力加速度g，所以升、降图线具有左右对称性，由图像可以直观地看出第一颗子弹与其他子弹相遇时所对应的是图中的A1、A2、A3、A4、A5点，相遇的时刻分别是t＝3.5s，4s，4.5s，5s，5.5s.

由于图线的交点都对应相遇点，显而易见，只要数一下每颗子弹的速率－时间图线与其他子弹的图线有几个交点，就可以得出它与几颗子弹在空中相遇.由图像容易数出：第1颗会相遇5颗、第2颗相遇6颗、第3颗相遇7颗、第4颗相遇8颗、第5颗会相遇9颗，从第6颗开始射出的子弹都会相遇10颗.

第（2）（3）问属于多颗子弹的相遇问题，不难想象，若采用公式计算，将会比较复杂.若采用我们惯常使用的速度－时间图像，则各子弹的图线也不会相交，不能用交点来形象地刻画相遇点.但巧妙地选用速率－时间图像，相遇点的情况在图像中一目了然，相遇的时刻及速度大小都能在坐标系中直接读出，方法巧妙，效果明显.

2 Ep－h、Ek－h 图像

某些能量会随距离呈线性变化，譬如重力势能、电势能、摩擦产生的内能等，都与距离有关.在涉及到有关能量随距离变化的问题时，我们可以巧用图像展示能量随距离变化的动态过程，往往从图像上就能一目了然、直观地得到结果，大大缩短了分析与推理的过程.

例2.在地面上以初速度v0竖直上抛一个足球，空气阻力不能忽略.足球在空中能上升的最大高度为hm，足球在上升过程距抛出点距离为h1处，足球的动能和重力势能相等，下落过程中距抛出点距离为h2处，足球的动能和重力势能相等，则列说法中正确的是

解析：本题涉及物体上升、下落两运动过程，两过程物体的动能、重力势能均随h变化而变化，属动态变化问题，较为复杂.抛出点所在的平面作为重力势能零势能面，以f表示空气阻力，h表示足球距抛出点的高度.在上升阶段，根据动能定理可得即

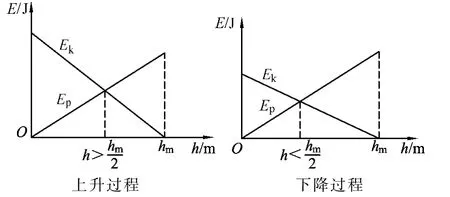
图2

在下落阶段，根据动能定理可得mg（hm－h）－f（hm－h）＝即

重力势能随h变化的关系式为

定性画出（1）（2）（3）式所对应的 Ep－h、Ek－h 图像，并在画图时注意：在上升阶段Ek＋Ep随h的增加而减小，在下降阶段Ek＋Ep随h的减小而减小，就可以分别画出如图2所示的图像.用图像可清晰展现动能、势能随h的动态变化过程，两图像交点表示两种能量相等的情景.则由图像不难直观地看出上升过程在处两种能量相等，下落过程在处两种能量相等.正确选项为（A）.

在闭合电路中，各量之间满足的关系是闭合电路的欧姆定律.对定律E＝U＋Ir作一下数学形式的变换，会衍生出多种表达形式，如等.这些表达式在近几年的高考试卷中屡有出现，尤其是在电学实验的考查中.如2009年北京理综卷第21题考查了图像，2009年广东卷第16题考查了图像（L系电阻丝的长度），2010年上海卷的第29题考查了图像，2010年江苏卷的第10题考查了图像，2011年江苏卷第11题考查了U－R图像，2011年山东理综卷第23题则考查了更为常见的U－I图像等.

例3.（2010年上海卷第29题）某同学利用DIS、定值电阻R0、电阻箱R1等实验器材测量电池a的电动势和内阻，实验装置如图3所示.实验时多次改变电阻箱的阻值，记录外电路的总电阻阻值R，用电压传感器测得端电压U，并在计算机上显示出如图4所示的关系图线a.重复上述实验方法测量电池b的电动势和内阻，得到图4中的图线b.

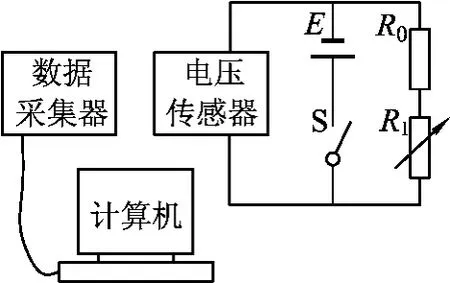
图3

（1）由图线a可知电池a的电动势Ea＝________V，内阻ra＝________Ω.

（2）若用同一个电阻R先后与电池a及电池b连接，则两电池的输出功率Pa_______________Pb（填“大于”、“等于”或“小于”）.两电池的效率ηa_______________ηb（填“大于”、“等于”或“小于”）.

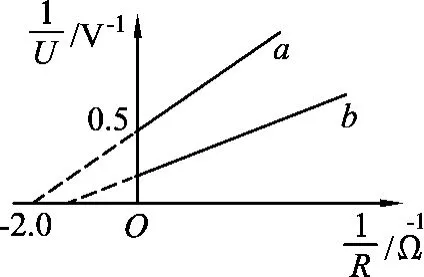
图4

有些物体的运动较为复杂，不是我们所熟悉的运动模型，无法用匀变速运动的规律来求解，其v－t图像也不呈直线.此时要解决问题，往往需要我们对两坐标轴所代表的量作灵活变动，目的是能把描述物体运动的图像“化曲为直”——变成直线，使直线的斜率、与坐标轴所围的面积等对应某些所求的物理量，用图像法实现突破.

例4.一只老鼠从老鼠洞沿直线爬出，已知爬出速度v的大小与距老鼠洞中心的距离s成反比，当老鼠到达距老鼠洞中心距离s1＝1m的A点时，速度大小为v1＝20cm／s，求（1）当老鼠到达距老鼠洞中心s2＝2m的B点时，其速度大小v2；（2）老鼠从A点到达B点所用的时间t.

图5

解析：因为老鼠从老鼠洞沿直线爬出，已知爬出的速度与通过的距离成反比，则不能通过匀速运动、匀变速运动公式直接求解，但可以通过图像法求解.在图像中，所围面积即为所求的时间.以距离s为横轴为纵轴建立直角坐标系，则s与成正比，作图像如图5所示，由图可得s＝2m时，老鼠的速度为10cm／s.在1m到2m之间图像与横轴包围的面积即为所求的时间，所以老鼠从A到B爬行的时间为

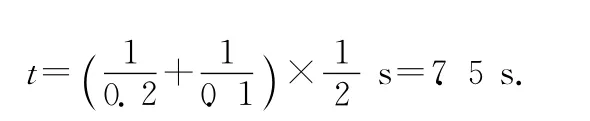
5.F－l图像

胡克定律的F－x图像为一条直线，其中x是弹簧的形变量，若把弹簧的原长记为l0，形变后的总长度为l，则x＝l－l0，我们还可以画出F－l图像，你习惯用F－l图像来解题吗？

例5.有一半径为3L且可以绕竖直轴转动的圆盘，盘内沿直径方向开有一条凹槽，凹槽内有一根劲度系数为k、原长为L的弹簧，弹簧的一端固定在圆盘中心，另一端系有质量为m的小球，今将弹簧拉长至d（L＜d＜3L）后，使小球与圆盘一起以角速度ω做匀角速转动，已知小球与槽底的静摩擦因数为μ，槽侧面光滑，μ与k 的关系为：5μmg＝3kL，若小球被拉至位置d，不管d在L＜d＜3L范围内取何值，小球对圆盘均能保持相对静止状态，求ω的取值.

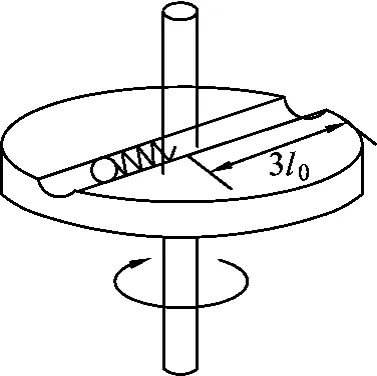
图6

解析：小球随圆盘一起以角速度ω做匀速圆周运动的所需向心力为

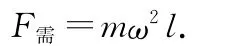
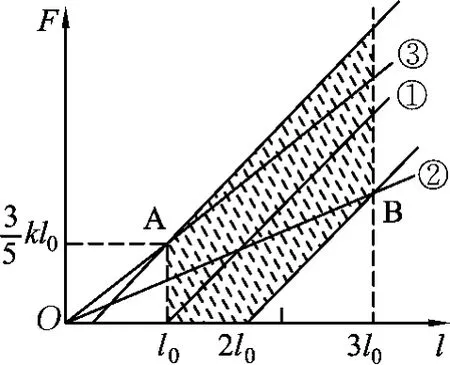
图7

小球做圆周运动的向心力要由弹簧弹力与摩擦力的合力来提供.

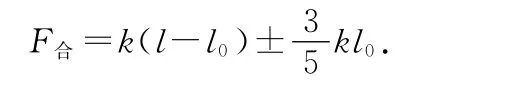
显然，F合为一定范围，只要小球在l0～3l0范围内所需的向心力F需不超出F合的范围，小球就能与圆盘保持相对静止.下面我们用图解法来解决该题.

在同一坐标系中分别作出F需－l及F合－l图像，如图7所示，图中过l0的直线①表示F＝k（l－l0）.由于F合＝k（l所以我们再在直线①的两侧作出与①平行且竖直相距皆为的两条直线，如图7所示，则图中阴影区即为F合的范围.

小球圆周运动所需向心力F需＝mω2l.当ω为某一定值而l为变量时，在F合－l坐标系中F需＝mω2l图像应为过原点的直线.选定不同的角速度ω就可以画出斜率不同的直线，其斜率随ω的增大而增大.为满足题目要求，即向心力F需不超出F合的范围，也就是说F需－l直线在l0＜l＜3l0时都应位于图7中的阴影内.由图示可知，满足上述关系的直线应在图中直线②和③之间.

直线②对应的是角速度的最小值，令其为ω1，则

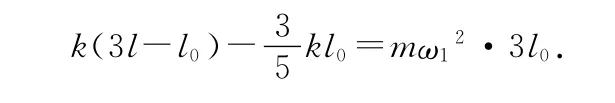
直线③对应的是角速度的最大值ω2，令其为ω2，则

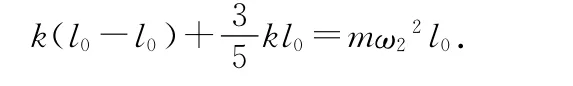
本题的物理情景颇为复杂，用常规方法将很繁杂.图像法使问题变得非常直观，通过直线② 和③ 与阴影区域的交点B和A很容易求出ω1和ω2，使我们有醍醐灌顶、恍然大悟之感.

6 a－t图像

若物理量A、B、C满足关系A＝B·C，我们可以建立平面直角坐标系，以纵坐标表示B，横坐标表示C，描绘出B、C的关系图像，则图线与横坐标轴所围的面积就可以表示物理量A.

例6.如图8所示，一个质量为m、带电荷量为＋q的物体处于场强按E＝kt规律（k为大于零的常数，取水平向左为正方向）变化的匀强电场中，物体与绝缘竖直墙壁间的动摩擦因数为μ，当t＝0时，物体由静止释放.若最大静摩擦力等于滑动摩擦力，且电场空间和墙面均足够大，求：

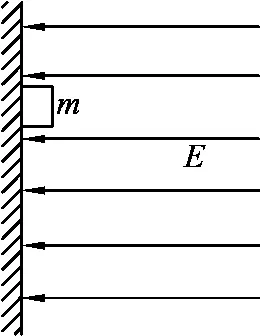
图8

（1）物体经过多长时间运动速度达到最大；

（2）最大速度是多少？

解析：在开始阶段，分析物体的受力可得mg－μqkt＝ma，随着时间的延续，物体的加速度越来越小，当a＝0时，物体的速度达到最大，此后做减速运动直至停止.所以在速度最大时有mg－μqkt＝0，即经过时间物体在竖直墙壁上的速度达到最大值.

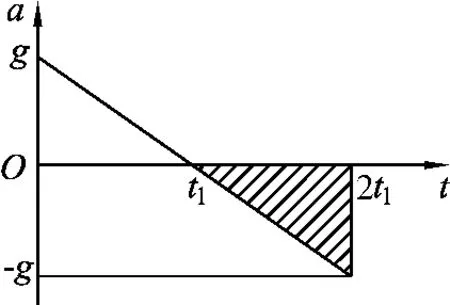
图9

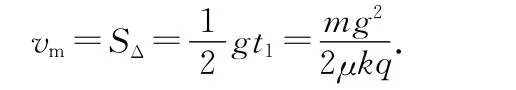
该题利用图像展示了复杂的动态过程，虽然不是我们所熟悉的匀变速运动，但可以根据图线与坐标轴所围面积的物理意义，简捷明快地得出了结果.简洁明了，令人耳目一新.

由此看来，图像往往都蕴含着丰富的信息，如图线的截距、斜率、拐点、图线所围面积、两图线交点等，往往都有各自的物理意义.巧借图像用之于解题，常常能化难为易、化繁为简，特别是有些运用解析法无能为力的问题，我们却常能从图像上触发灵感，另辟蹊径，使问题变得迎刃而解，具有难以替代的作用.运用图像解题也是高考重点考查的能力之一.作为教师，在课堂教学中尝试着渗透图像法，把解析法与图像法有机结合起来，有意识地引导学生进行图像法解题的思维与训练，是培养学生掌握图像法解题的关键所在.