基于曲率的GPU光线投射

袁 斌

（北京应用物理与计算数学研究所，北京 100088）

基于曲率的绘制十分有用，它可以帮助科学家分析曲率分布，设计新的计算模型。曲率可以用来表现线状特征和粒状特征。K. Gordon等在CPU中实现了基于B样条滤波的曲率计算[1]，但计算速度较慢。采用 GPU可以大大加速曲率的计算。

现代 GPU已经发展成为众核处理器，具有强大的计算能力和高内存带宽。在一般的图形卡上，采用多条绘制流水线，可以对顶点(vertex)计算和片元(fragment)计算进行并行处理。采用GPU可以大大加速体绘制，如基于切片的体绘制方法[2-4]和GPU的光线投射方法[5-7]。预先计算一阶导数、二阶导数，需要占用大量的存储空间（存储梯度和Hessian矩阵），这显然是不能接受的。因此需要实时计算他们。

本文在GPU上实现了基于线性滤波的曲率计算方法和并将C.Sigg方法结合到GPU光线投射方法中，按需计算导数，曲率和光照效果。在线性滤波情况下，一阶导数和二阶导数无法精确计算，只能采用差分方法。在三三次B样条滤波条件下，可以精确计算标量，一节导数、二阶导数。本文给出有效的计算曲率的方法。设计多种关于曲率的函数，实现了交互选择曲率函数，突出感兴趣特征的方法。

1 相关工作

S. Stegmaier给出单趟GPU光线投射方法[5]。该方法预先计算梯度并保存起来，这样必然占用大量的内存。在透视投影下，光栅化时如果直接采用线性插值，就不能正确计算片元的颜色、纹理坐标等属性，为此OpenGL对插值算法作了修正,这样它可以正确计算片元的属性[8]，这是基于代理面的GPU光线投射的基础。T. Klein给出结合预积分的GPU光线投射方法[6]，通过绘制体的前表面得到光线的起点，起点减去相机的位置（在纹理空间）得到光线的方向。Scharsach的论文[7]把体包围盒顶点坐标转换成颜色，并设置为顶点颜色。绘制前面和后面到不同的缓冲区，后面的图像减前面的图像，得到光线方向，并根据这个方向进行光线积分。该文还设计基于块的空区域跳跃方法，通过深度测试，把第一前面和最后一个后面绘制到不同的缓冲区中，这样在光线积分时可以跳过前面和的后面的空区域，提高了光线投射的速度。郑杰等在纹理切片体绘制方法中，采用实时计算梯度的方法[9]，大大节省纹理内存，适合于大规模数据场，是很好的方法。K.Gordon等[1]在CPU中实现了基于B样条一阶导数、二阶导数以及曲率计算，但计算速度较慢。C.Sigg等[10]在GPU中实现基于B样条的一阶导数、二阶导数快速计算，并应用到最大主曲率的计算；并把该方法与等值面绘制结合，绘制速度很快；但未把该方法与光线投射体绘制结合。

2 基于曲率GPU光线投射

本文实现基于曲率的可视化，要计算隐式曲面的曲率，需要计算Hessian矩阵和梯度。

一阶导数，二阶导数计算采用实时计算方法。如果预先计算各种导数，每个网格节点需要保存3个一阶导数，3个二阶导数，和3个二阶偏导数，需要多存储9个数据，若采用单字节表示，另外需要 1个字节保存梯度量，则需要 10个字节，存储量将是本文方法的 11倍。采用这种方法，精度很低，会降低绘制质量。若采用浮点数表示标量和导数，存储量为本文方法的 37倍。对较大的数据，如 Xmas-Tree，不可能装入到纹理内存。因此，不能采用预计算一阶导数，二阶导数的方法。

2.1 基于B样条滤波的按需计算导数的方法

在线性滤波条件，采用近似的导数计算公式，而在B样条滤波条件下，存在精确的导数计算公式。当用B样条滤波重构数据场时，本文采用 C.Sigg方法快速计算标量和导数[10]。这里分析一下C.Sigg的方法的邻点数并进行优化处理。

如图1所示，计算标量需要8个邻点，计算梯度需要24个邻点，计算二阶偏导数需要24个邻点，计算二阶导数需要计算36个邻点。用Tex指令取出邻点上的标量值。

图1 C.Sigg 方法

计算导数和曲率需要大量的计算，本文按需计算导数，曲率和光照。这样可以大大加速计算。在GPU光线投射算法中,用C.Sigg方法计算标量值，需要用8个Tex指令取出当前采样的（8个）邻点上标量值，结合前一采样点的标量值，得到当前积分步的不透明度，如果不透明度为非0，用 C.Sigg方法计算计算导数，需要用 84个Tex指令取出（84个）邻点上标量值，然后计算曲率以及光照效果。这样有效地加速绘制过程。

2.2 基于线性滤波的按需计算导数的方法

目前的 GPU已经实现基于线性滤波的纹理映射，没有实现基于高次滤波的纹理映射。在线性滤波条件下，近似计算各种导数。

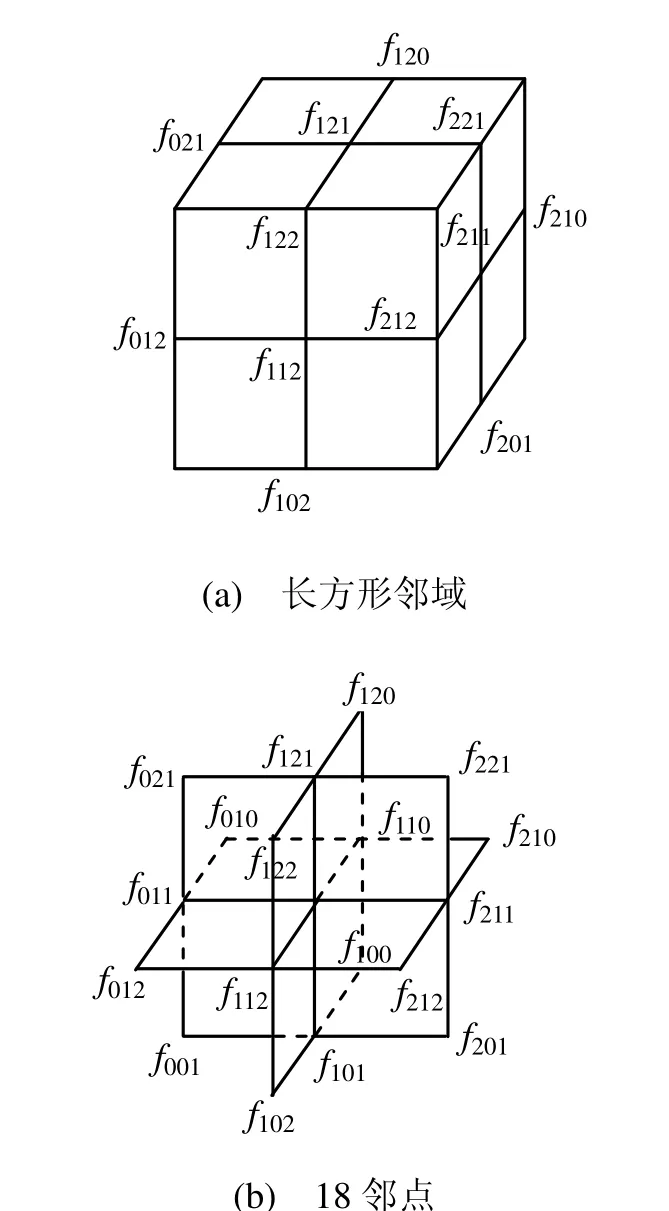
图2 领域和邻点示意图

考虑以采样点为中心的2×2×2轴向长方形网格D，其网格间隔与被处理的网格一致，D被称为采样点的邻域，其节点数为3×3×3，节点上的物理量记为其中f111等于光线段上当前采样点的值。因为光线段上的采样点一般不在网格节点上，所以，D的节点一般情况下，位于原网格单元的内部，而不是在节点上。采用中心差分计算一阶导数和二阶导数需要18个邻点，以光线采样点为中心，取18个邻点,如图2(b)。邻点的物理值通过三线性插值计算，通过纹理映射实现。采用向量指令计算梯度和Hessian矩阵，用一个向量保存对角元素( fxx,fyy,fzz)，另一个向量保存( fxy,fyz,fzx)

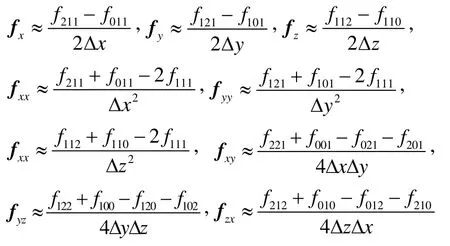
在光线投射算法中，先用1个指令取出当前的标量值，结合前一采样点的标量值，得到当前积分步的不透明度，如果不透明度非0，采用18邻点方法，计算梯度，Hessian矩阵和曲率，是一个实用的方法。

2.3 曲率计算方法

称为总曲率. 将 trace(P HP(P HP )T)直接展开比较麻烦。采用矩阵计算会简捷一些，但仍然需要采用较多步数，因此，不同于文献[1]，本文不直接计算，而是先计算高斯曲率，下面给出高斯曲率公式的简单推导过程

这样，可以用向量乘法和DP3指令实现以上公式[11]。导数、二阶导数和曲率均在物理空间计算，而不是在图像空间计算。在计算出b和c后，就可以计算主曲率。

主曲率可以描述曲面的局部特征，根据主曲率，曲面上的点可以分为椭圆点，双曲点，和抛物点。曲面的几何特征如“沟谷”，“山脊”，“山峰”，“洼坑”，线状特征和粒状特征等与曲率密切相关。根据需要设计关于主曲率的函数F(κ1,κ2)，来突出感兴趣的特征。

2.4 曲率GPU光线投射的实现

实现基于代理面的 GPU光线投射体绘制的基本步骤是：

1）把数据场装入GPU内存；

2）装入写缓冲区和光线积分片元程序；3）连接写缓冲区的片元程序；

4）绘制数据体的后表面到FBO；

5）连接GPU光线投射的片元程序；

6）设置GPU光线投射程序的局部参数；7）绘制数据体的前表面。

开始时，实现基于B样条滤波的曲率GPU光线投射，未考虑按需计算导数，绘制速度较慢。为了加速绘制，采用按需计算导数的方法。

F为关于主曲率的函数，向量v的x,y分量分别保存当前积分步两端的标量值。基于曲率的GPU光线投射算法如下：

算法1 基于曲率的光线投射算法

把当前纹理坐标(即当前光线与前面的交点)保存到tex0;

置光线累积透明度为0;

从FBO中取出背面上的纹理坐标，即当前光线与数据体后表面的交点;

计算光线方向;

修正采样步长;

计算当前光线总的积分步数;

计算单步增量;

LOOP (255,0,1){

LOOP (255,0,1){

将当前采样点的坐标变换到基本纹理空间;

计算当前采样点的标量值scal;

if(当前采样点是第一个采样点)v.x = scal;

否则{

当前积分步终点标量值v.y = scal;

用v查预积分表得到不透明度;

v.x = scal;

如果当前积分步不透明度非0{

用SIMD方法计算标量、法向量、

偏导数和二阶导数;

计算法向量的模;

采用SIMD方法计算高斯曲率和主曲率之和；

计算F;

规格化梯度量；

根据梯度量查调制因子;

将F转换为颜色;

用当前积分步的不透明度预乘颜色；

计算光照；

用当前积分步的不透明度修正镜面光；

用梯度量调制环境光、漫反射光和镜面光；

累积颜色；

调制当前积分步的不透明度；

累积光线段的透明度；

如果累积透明度小于0.02,退出循环；

}

}

前进一步;

如果累积步数等于总步数，退出循环；

}

}

计算光线不透明度；

输出颜色和不透明度；

注：LOOP (255,0,1)表示循环255次。

在GPU光线投射的片元程序中实现算法1，算法采用按需计算导数的方法。根据当前采样点的标量和前一采样点的标量，查预积分表取得当前积分步的不透明度，只有不透明度非0时，才计算梯度、Hessian矩阵、曲率和光照。计算标量时，如果采用线性滤波，用一个Tex指令取出当前采样点的标量值[11]；若采用B样条滤波，用8个Tex指令取出8个邻点。在计算导数时，若采用线性滤波需要18个邻点；若采用B样条滤波，需要 84个邻点。颜色转换函数把关于主曲率的函数F(κ1,κ2)转换成颜色。颜色转换函数和预积分表用纹理实现。用 GPU快速计算预积分[12]，这样可以交互修改转换函数。函数F的值紧缩到[0.02,0.98]，如果它大于 0.98,置为 0.98;如果小于0.02,置为0.02。

本算法充分利用SIMD技术进行计算。采用光线早中止加速绘制过程。在本文中，采用SIMD方法计算高斯曲率和主曲率之和，只需要 17条指令。计算高斯曲率的一些中间结果可以用来计算主曲率之和。temp3保存二阶导数，temp5保存二阶偏导，normal保存法向量。temp2.x为法向量模的平方。下面是相关的程序段。

MUL temp8,normal,normal;

ADD temp9,temp8.yzxw,temp8.zxyw;

DP3 temp9.x,temp9,temp3;

MUL temp7,temp3,temp3.yzxw;

DP3 temp4.x,temp7,temp8.zxyw;

MUL temp7,temp5,temp5;

DP3 temp4.y,temp7,temp8.zxyw;

MUL temp8,normal.yzxw,normal.zxyw;

DP3 temp9.y,temp5,temp8.zxyw;

MUL temp7,temp5,temp5.zxyw;

DP3 temp4.z,temp7,temp8;

MUL temp7,temp3,temp5.yzxw;

DP3 temp4.w,temp7,temp8;

DP4 temp6,temp4,{1,-1,2,-2};

DIV temp6,temp6,temp2.x;// 计算高斯曲率;

DP2 temp10,temp9,{1,-2,0,0};

MUL temp10,temp10,temp1.x;;// 计算主曲率之和;

我们已经基于 VTK[13]实现了一个可视化原型系统，将本文算法集成到原型系统中进行测试。在原型系统中，实现了修改转换函数以及保存、恢复交互参数的功能。

在GPU光线投射中，采用高次B-样条滤波可以起到光顺作用，消除走样现象，绘制质量很好。但是由于采用B样条滤波，计算量较大，绘制速度较慢。本文同时实现了基于线性滤波和B样条滤波的按需计算导数的GPU光线投射方法。在原型系统中，增加了选择曲率函数的交互功能；修改保存和恢复功能，使之包括曲率函数。

在交互过程中，先采用基于线性滤波的绘制方法交互选择必要的相机参数、转换函数和曲率函数，再用基于B样条滤波的方法绘制高质量图像。

3 实验与分析

本文在GPU上实现了基于线性滤波和B样条滤波的按需计算导数、曲率和光照效果的光线投射方法，分别记为LRT和BRT,为了便于比较，还实现了基于B样条滤波的非按需计算导数（曲率和光照效果按需计算）的光线投射方法，记为BRTN。本文在装有NVIDIA NVS 4200M 显卡的intel i5机器（便携式电脑）上测试算法。以下测试中，除非有特殊声明，采样步长为最小网格间隔的1/4光线积分计算中，采用光线早中止技术，不透明度决定了实际的采样步数，颜色转换函数不影响采样步数。在测试绘制速度时，对一种数据，选择一个曲率函数即可。在测试过程中，本文利用基于线性滤波的光线投射方法 LRT交互选择相机设置、各种转换函数和曲率函数，突出感兴趣的特征，然后用基于 B样条滤波的方法BRT绘制高质量的图像。

图3(a)与图3(b)绘制质量相同，图3(b)速度更快。B样条滤波可以更好地突出特征，如图3(b)所示，而线性滤波淡化了特征，如图3(c)所示。从图3可以看出，+0.4可以较好地表现线状特征（绿色）。图4为head数据，采样步长为最小网格间隔的1/16，采用B样条滤波，管状特征很光滑；而采用线性滤波，图像质量可以接受。图5(a)与图5(b)绘制质量相同，图5(b)速度更快。B样条滤波可以更好地突出特征，如图5(b)所示，而线性滤波淡化了特征，如图5(c)所示，适当调整颜色转换函数可以增强特征。从图5可以看出，高斯曲率可以较好地表现粒状特征（红色或绿色）。这些粒状特征是由噪声引起的。高斯曲率可以分析噪声的分布。

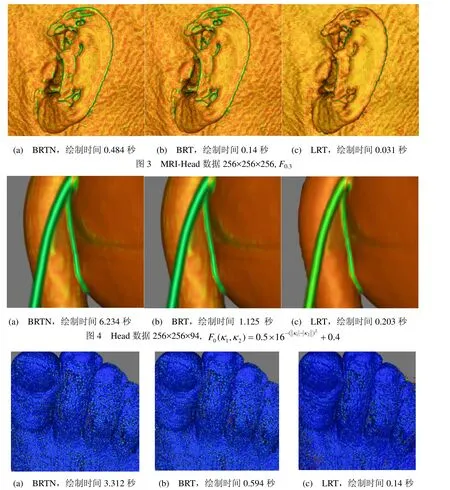
图5 foot 数据256×256×256，高斯曲率Fg

如图6(a)，图6(b)所示，绘制质量相同。基于B样条滤波F0函数可以很好表现松针。如图6(c)所示，基于线性滤波，F0也可以表现松针，但质量较差。F0可以用于提取线状特征。

图6 Xmas-Tree 数据 512×512×999，F0

如图 7(a)所示，平均曲率 Fm既可以表现线状特征，又可以表现粒状特征；图7(b)采用总曲率Ft突出了线状特征。

由表1可以看出，按需计算可以大大加快绘制速度，线性滤波快于B样条滤波。采用线性滤波可以进行交互绘制。

LRT先用1个Tex指令取出当前的标量值，结合前一采样点的标量值，得到当前积分步的不透明度，如果不透明度非0，采用18邻点方法，计算梯度，Hessian矩阵和曲率，是一个实用的方法。BRT用C.Sigg方法计算标量值，需要用8个Tex指令取出当前采样的(8个)邻点上标量值，结合前一采样点的标量值，得到当前积分步的不透明度，如果不透明度为非0，用C.Sigg方法计算计算导数，需要用84个Tex指令取出（84个）邻点上标量值，然后计算曲率以及光照效果，从而有效地加速绘制过程。BRT绘制质量比基于LRT好，LRT速度比BRT快。本文的方法可以交互选择曲率函数，突出感兴趣的特征，从而帮助科学家有效地分析数据。

图7 平均曲率和总曲率的绘制效果(BRT绘制)

表1 绘制时间比较

[1] Kindlmann,G,Whitaker R,Tasdizen T,et al. 2003 Curvature-based transfer functions for direct volume rendering: Methods and applications[C]//Proceedings of IEEE Visualization,2003: 513-520.

[2] Cabral B,Cam N,Foran J. Accelerated volume rendering and tomographic reconstruction using texture mapping hardware [C]//Proceedings of the 1994 Symposium on Volume Visualization,New York,NY,USA,ACM Press,1994: 91-98.

[3] Engel K,Kraus M,Ertl T. High-quality pre-integrated volume rendering using hard-ware-accelerated pixel shading [C]//Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Workshop on Graphics hardware,2001: 9-16.

[4] 童 欣,唐泽圣. 基于空间跳跃的三维纹理硬件体绘制算法[J]. 计算机学报,1998,21(9): 807-812.

[5] Stegmaier S,Strengert M,Klein T,et al. A simple and flexible volume rendering framework for graphics-hardware-based raycasting [C]//Proceedings of the International Workshop on Volume Graphics'05,Stony Brook,New York,USA,2005: 187-195

[6] Klein T,Strengert M,Stegmaier S,et al. Exploiting frame-to-frame coherence for accelerating highquality volume raycasting on graphics hardware [C]//Proceedings of IEEE Visualization,2005: 223-230.

[7] Scharsach H. Advanced GPU raycasting [C]//Proceedings of Central European Seminar on Computer Graphics 2005,Budmerice Castle,2005:69-76.

[8] Segal M,Akeley K. The OpenGL graphics system: a specification [EB/OL]. 2004.http://www.opengl.org/documentation/specs/

[9] 郑 杰,姬红兵. 基于动态纹理载入的大规模数据场体绘制[J]. 中国图象图形学报,2008,13(2):316-321.

[10] Sigg C,Hadwiger M. Fast third-order texture filtering [C]//Book Chapter in GPU Gems II,Matt Pharr(ed.),Addison Wesley,2005: 313-329

[11] NVIDIA. NVIDIA OpenGL extension specifications. 2011. https://developer.nvidia.com/nvidia-opengl-specs

[12] 袁 斌. 改进的均匀数据场 GPU 光线投射[J]. 中国图象图形学报,2011,16(7): 1269-1275.

[13] Martin K,Schroeder W,Lorensen B. The Visualization ToolKit(VTK)[EB/OL]. 2008. http://www.vtk.org/