一种基于CAD的翼类曲面误差检测方法

刘子路， 张 俐， 郑国磊

（北京航空航天大学机械工程及自动化学院，北京 100191）

机翼作为为飞机提供升力的重要部件，其外形准确度关系到飞机是否具有良好的气动升力和阻力特性，以及具有良好的稳定性。因此机翼型面误差检测是翼类部件装配过程中控制其装配质量的关键环节之一。

目前国外航空制造领域在装配过程中已经大量采用非接触式光学测量、定位技术及设备进行飞机部、段件的精准装配[1]。而国内航空制造企业，大尺寸部件型面的装配误差检测基本上仍采用的是传统的样板检测方式，这种检测方法存在着，对机翼曲面型值偏差和波纹度的检测精度较低；只能对某一特定型号部件进行检测，缺乏柔性，成本较高；检测结果为模拟量数据，不便于在装配过程中进行实时精确的装配调整等问题。

有鉴于此，本文针对机翼部件研究了一种基于CAD模型的机翼外形曲面误差检测与计算方法，通过该方法可以较快速地获得机翼零部件的曲面型值偏差，为零部件装配过程中的调整提供依据。

1 原理概述

在现代飞机制造中，飞机设计都是通过数字化设计来完成的，通过设计模型可以获得机翼的理论外形曲面。数字化装配过程中，使用激光跟踪仪和激光扫描仪可以得到机翼曲面的实测点云数据。利用装配基准点对理论曲面和实测点云拟合而成的测量曲面进行配准，进行误差计算获得结果即为装配误差。本文提出了一种计算点云中到理论曲面上指定点的距离最小的点，并将该最小距离到曲面上指定点处法矢方向投影长度作为曲面误差的曲面误差计算方法。

测量数据处理与误差计算流程如图1所示。

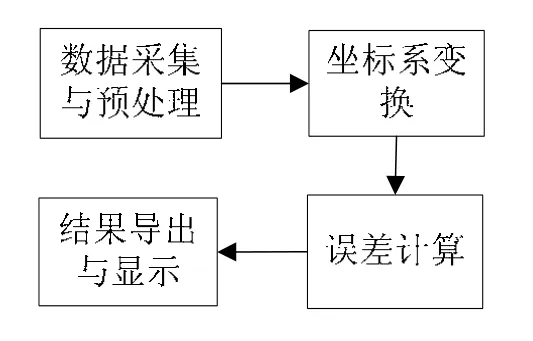
图1 检测方法流程图

2 数据采集与预处理

数据采集是通过特定的测量设备获取产品表面离散点的空间坐标数据。测量设备根据测量时测量探头或传感器是否与实物接触可分为接触式和非接触式两类[2]。目前常用的接触式测量系统有三坐标测量仪（CMM），其测量精度高，但不适合测量外形复杂的型件，也不便于进行装配过程中的在线测量；非接触式测量系统有激光测量系统、照相式快速扫描测量系统等。

本研究采用激光测量系统完成对翼面及装配基准点的三维数据测量。在测量时，在翼面边缘处可能产生噪声，因此需对检测数据做去噪处理；为保证检测精度，通常采用密集的采样方式，而在误差分析时为提高计算效率通常需要分布均匀且数量不多的点。因此在进行计算前需对检测数据进行精简[3]。

为避免产生拟合误差，不对测量曲面进行重构，而采用从测量的数据点集中提取采样特征点直接进行计算的方法。

3 坐标系变换

坐标系转换就是实现测量坐标系与理论坐标系的配准，其配准精度直接影响到后续误差结果的可靠性。目前常用的坐标配准方法有遗传算法、力矩主轴法、三点对齐法和最小二乘法。前两种配准效率较低，三点对齐法原理简单能够较快实现初始配准，但是必须准确的确定出三对基准点的对应关系，并且基准点的测量误差对配准精度的影响非常大[4]。最小二乘法利用多个基准点进行配准，可以在一定程度上消除基准点测量误差，因此在本研究采用最小二乘法实现坐标系的转换。

在理论模型中设计不共线的一系列点TB1、TB2··TBn作为基准点，其在理论坐标系中的坐标值分别为 p1、p2··pn，在实际装配环境中依据设计模型设置基准点，这些点在测量坐标系中的坐标为 q1、q2··qn，则通过如下的矩阵变换可以将测量坐标系中的测量数据转换到理论坐标系下

其中，R为旋转矩阵，T为平移矩阵。

由于加工误差和测量误差的存在，测量获得的基准点间的相对位置不可能与理论值完全一致，因此坐标变换关系可表示为

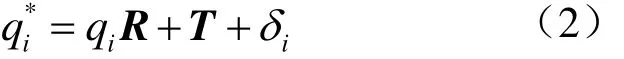
根据参考文献[5]中所提出的矩阵奇异值分解法可求得式(3)的最小二乘解和。

对测量坐标系中的测量获得的点集 Q进行坐标变换，将其变换到理论坐标系下

得到变换后点集P。

4 误差计算与显示

目前常用的曲面型值偏差计算方法是使用检测点云数据拟合曲面，然后计算理论曲面上一点到拟合曲面最短距离的误差计算方法。这种方法在拟合过程中会引入拟合误差，从而影响计算结果的准确性。本文提出了一种利用点云数据直接进行计算的型值偏差计算算法。

4.1 算法概述

机翼曲面曲率较小，且经配准后曲面误差远小于该点处曲率半径。本文针对机翼外形曲面这一特点，提出了一种利用检测点云直接进行误差计算的方法。

设产品理论曲面为S(u,v)，其中u,v为曲面参数，则理论曲面上任意点pt处的法矢可表示为[6]

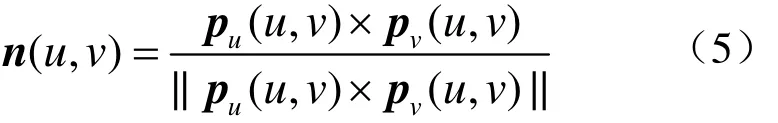
其中, pu(u,v)、pv(u,v)分别为pt处的u向偏导矢和v向偏导矢。

pt到点云 Pc的距离记为Dm

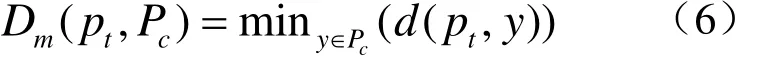
其中， d ( pt,y)为点pt和点y的欧氏距离。

将 Dm( pt,Pc)向n(u,v)投影获得的距离值 D便可近似为pt点处的误差值(如图2所示)。

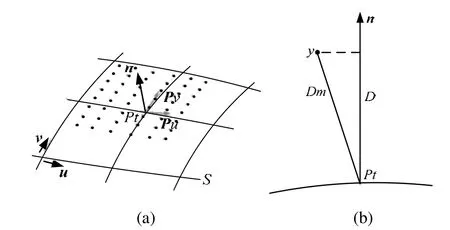
图2 误差计算算法原理图

4.2 曲面曲率、点云密度与计算精度关系分析

设Pt处曲率半径为R，点云间距为d，计算误差为Δ（如图3所示），

则三者之间的关系式为

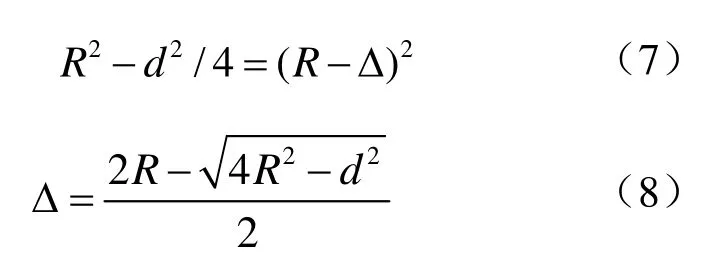
由式(8)可知，Δ随 R增大单调递减、随 d增大单调递增。

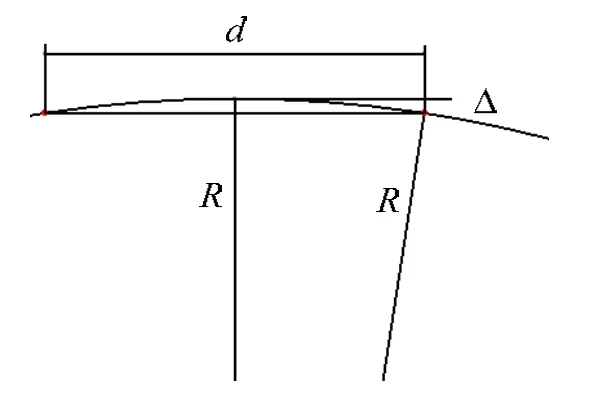
图3 算法误差示意图

在实际测量中点云间距可达到 10微米，而测量曲面上曲率最大处曲率半径约为5mm，由此可算得曲面上最小计算误差0.0025um，该误差在曲面精度要求范围内，完全可以满足检测精度要求。

4.3 计算效率优化

该算法在计算过程中需要遍历点云中所有的点，时间复杂度为O(n)，当点云数量巨大时，会严重影响计算效率。

为提高计算效率，首先可以在在曲率较小的区域对点云进行稀疏，减少总体点云数量，以在不影响计算精度的前提下提高算法效率。

对点云进行遍历，求取最优点pb的一般计算方法有如下两种：

1）方法1

（1）计算点云Pc中任一点p1距pt法矢的距离，将其记为Dm，将p1记为pb；

（2）对 Pc中其他点 pt进行遍历，若 pi与pt法矢之间的距离小于Dm，则将其记为Dm，将pi记为 pb；

（3）遍历结束，所求最优点为pb。

方法1中，对点云中的所有点进行了遍历，并计算点与直线间的距离。为提高计算效率，在遍历前，可先缩小搜索的范围，然后进行计算。计算方法如下：

2）方法2

（1）以pt为中心，允许最大误差Δ的二倍为边长构造立方体，并计算点云中所有位于该立方体内的点的集合，将其记为；

（4）遍历结束，所求点为pb。

对上述两种方法进行比较，采用方法2在点数量较大时、立方体区域足够小时可明显提高计算效率。

4.4 误差显示

为直观显示曲面误差的分布，对计算结果进行色彩显示。规定测量点位于曲面法矢所指方向一侧时，误差值为正，反之为负。使用颜色分布图来直观显示误差分布，将正向最大误差用红色表示、误差为0处用绿色表示、负向最大误差用蓝色表示。

5 实 例

利用文中所述检测方法对机翼部件曲面进行误差检测。图4给出了截取的翼类局部曲面计算实例。

检测原始点云数据如图4(a)所示。对原始点云进行去噪、简化等预处理，并将其导入到检测程序中，显示结果如图4(b)所示，然后对点云进行坐标变换，使其与理论曲面配准，配准结果如图4(c)所示，图4(d)为计算结果显示图：红色表示正向误差最大，蓝色表示负向误差最大，绿色表示误差最小（为0）。

该方法的计算结果精度可达 10-3mm。表1所示按纵向百分线统计的误差表，图5为根据误差数据绘制的曲线图，100%参数线为曲面边缘，误差不符合整体误差规律，将其剔除。该曲面部件纵向长度为260mm，由测量数据可知该曲面绕44%参数线转角约0.2°。

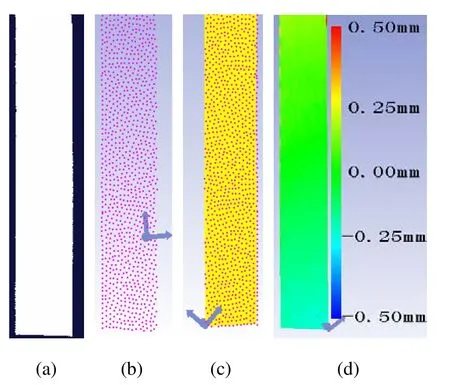
图4 某翼类曲面检测实例图

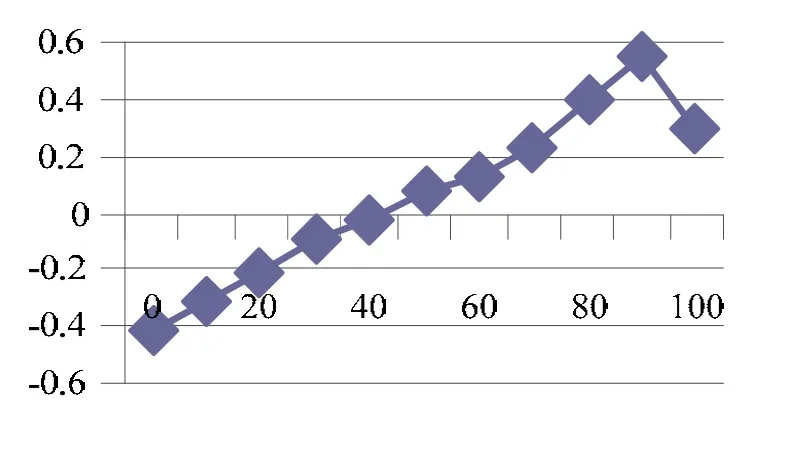
图5 曲面误差曲线图

6 结 论

本文研究了一种基于 CAD的 数字化检测方法，针对翼类曲面的型面误差检测研究了一种误差计算的快速算法，并开发了相应的检测程序。该方法可以快速准确地计算翼面形状误差，并能实现误差分布的直观色彩显示。经实验验证，该算法在保证计算效率的前提下，检测精度完全可以满足机翼部件装配精度要求。

[1] 郭恩明. 国外飞机柔性装配技术[J]. 航空制造技术,2005,(9): 28-32.

[2] 许国康. 大型飞机自动化装配技术[J]. 航空学报,2008,29(3): 734-740.

[3] 罗大兵,高 明,王培俊. 逆向工程中数字化测量与点云数据处理[J]. 机械设计与制造,2005,(9):56-58.

[4] 方 芳,宁 涛. 产品制造误差的数字化检测[J].航空精密制造技术,2004,40(1): 37-40.

[5] Arun K S,Huang T S,Blostein S D. Least square fitting of two 3-D point sets [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1987,9(5):698-700.

[6] 施法中. 计算机辅助几何设计与非均匀有理 B样条[M]. 北京: 高等教育出版社,2001: 443-444.