一种基于点集自适应分组构建Voronoi图的并行算法

王结臣， 蒲英霞， 崔 璨， 陈 刚， 马劲松

（江苏省地理信息技术重点实验室，江苏 南京 210093；南京大学地理信息科学系，江苏 南京 210093）

Voronoi图是计算几何中的一个经典数学问题，它在地理信息系统、气象学、生态学、分子生物学等学科有着较成熟的应用，自动构建Voronoi图也因此得到较多的研究[1-4]。针对点线面体等多维空间实体的Voronoi图生成[5-7]都有着广泛的研究，其中平面点集的Voronoi图应用最为广泛，其生成算法主要有增量算法、扫描线算法、分治算法等几种。

增量算法[8-9]是较早建立的一类Voronoi图生成算法，它通过逐个加入点，并局部修改Voronoi图结构信息来构造新的Voronoi图。增量算法设计思路简单，易于实现，且Voronoi图的动态更新较为容易。但其时间复杂度为 O(n2)，在数据量较大的情况下，难以满足实际应用。

扫描线算法[10]是Fortune于上世纪80年代提出，它给定一条垂直扫描线对平面点集从左至右进行扫描，每扫过一个点就为该点构造一条以扫描线为基线的抛物线（称之为点事件），离扫描线最近的一些抛物线在相交和连接后可构造出一条岸线（Beach Line）。随着扫描线的推进，岸线形状不断改变。当岸线上某交点到扫描线距离与到该交点对应的两平面点距离相等时，获得Voronoi图多边形的顶点（称之为圆事件）。按此思路，将扫描线推进到平面点集最右端，Voronoi图构建完成。

分治算法最早由 Shamos和 Hoey提出[11]，该算法预先将平面点分为若干组，为每个组生成各自的Voronoi图后，再进行合并。具体实施步骤是将所有点按照x值进行排序，使用一条垂线将点分为两组，每组点数大致相等，分别将两组点生成 Voronoi图，最后在垂线处实现 Voronoi图的合并。该算法一般通过递归方式分组，即在子组内构造垂直线完成进一步分组。垂线两侧的图形合并采用构造分割链的方法实现，将分割链两侧的完整边和非完整边剔除，并把分割链补充给新的Voronoi图，实现合并。Oishi等在此基础上将Voronoi图中元素的拓扑方向引入计算，以提升分治算法速度，取得了一定的效果[12]。

一些学者从其他角度入手研究Voronoi图的生成及其重要性质，如凸包距离函数法[13]、递归算法[14]、离散Voronoi图算法等[15-16]，这些研究对Voronoi图生成也取得了较好的效果。

随着计算机数据处理规模的不断增大，现有方法越来越难以满足应用需求，针对海量空间数据的高效计算方法成为新的研究重点。当代计算机在多核、分布式技术等方面的发展，使Voronoi生成算法在并行环境下的实现成为可能。在将并行计算技术引入Voronoi图的生成方面目前也有一些研究成果，如 Cole等在分治算法的基础上进行并行计算[17]，Ulrith等采用凸包距离函数实现了一种随机并行算法[16]。然而，受当时软硬件条件限制，现有的并行算法多着重于理论分析，算法测试数据量较小，一些研究由于受计算环境的限制难以推广应用。此外，已有的并行算法通常以分治法为基础，此时分组形状不易控制，易形成狭长的条带，在进行分组子网合并时会出现大量边界点，导致子网间出现过多未封闭多边形，在一定程度上影响了算法的整体效率。

为此，本文在分析分治算法思想的基础上，考虑将平面点集进行自适应网格划分，使得每个分组中点的数量近似相等，且尽量避免每个矩形分组出现狭长条带。同时，考虑到扫描线算法作为一种较经典的Voronoi图生成算法，其时间复杂度为 O(nlgn)，算法性能和稳定性都比较好。本文采用其作为各点集分组的子网生成算法，并采用并行计算方式完成这一过程。在相邻网格之间，依据扫描线算法中的岸线理论提取边界点，将边界点集生成Voronoi图并更新原图所在的多边形边以完成多边形的合并。

1 平面点集自适应分组

1.1 自适应分组

为加快平面点集Voronoi图生成的效率，较有效的策略是对点集进行空间分组，而后进行分组间Voronoi图的合并。这种“各个击破”的策略在诸多空间分析算法中有应用范例，如分组构建凸包、分组生成TIN等。

图1 基于格网的二维平面点集分组

如图1所示，点集被分配到6行×9列的空间网格中，若将每个分组单独生成Voronoi图，则后续处理只需完成组与组之间的Voronoi子图合并即可。这种分组策略与常见的分治算法有一定的相似之处，它也体现了一种分而治之的思想。

规则格网分组在一定程度上可提高原算法的效率，但当点的空间分布不均匀时，会导致各网格内点数差异太大，影响算法执行的整体效率。尤其是进行算法并行化实现时，这种影响尤为显著，此时由于各组耗时相差太大，导致处理器之间难以均衡而降低计算效能。

图2 平面点集自适应分组

为避免现有分治算法中采用沿扫描线单方向进行分组易形成狭长条带等问题，同时借鉴规则网格分组的思想，本文设计了一种基于二叉树的点集自适应分组方案。如图2所示，假设分组后最小点集中点数不少于20，首先为二叉树设定根结点（图2中I(1)），该结点覆盖原始点集；然后以一条水平分割线将该初始网格单元一分为二，两个子单元中点数近似相等；再后分别针对上述每个子网格单元分别采用一条垂向分割线进行划分，依此类推，直至网格单元中的点数小于预设值2倍时终止分割，得到最终的叶子结点。划分过程中采用水平还是垂直分割线，主要取决于网格单元的长宽。该过程很容易使用递归方式实现，图3为图2的二叉树分裂示意图。

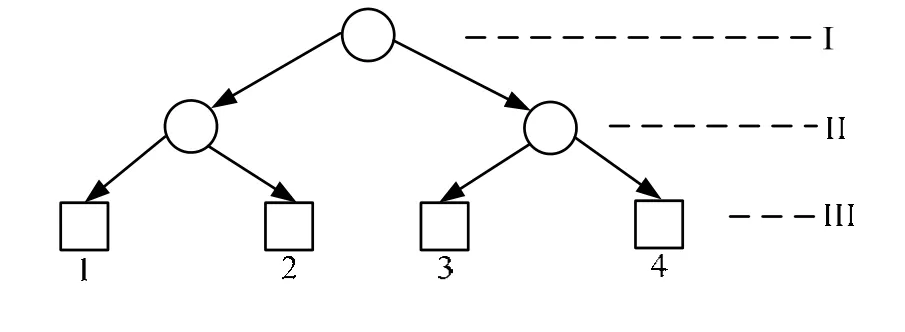
图3 平面点集分组的二叉树表达

1.2 数据结构

笔者称上述方法为“基于二叉树的点集自适应分组”，在数据组织时，按算法中需要表达的空间要素从小到大可分为4个层次：平面点集、Voronoi边、Voronoi多边形和二叉树矩形网格（限于篇幅，本文省略了Fortune扫描线算法中的几个中间过程结构体），其中二叉树网格只有在其叶子结点上才赋值，其他单元赋值为空。这些结构体用C语言可描述为下述形式（见1.2节）。

//平面点结构体

//点的平面坐标

//该点在网格单元中的编号

//该点在整个平面点集中的编号

//Voronoi边结构体

//构成该边的直线方程系数

//Voronoi边构成的线段的两端点坐标

//Voronoi边两侧所对应的两个原始平面点

//标记该边所在的线段是否与矩形网格单元边界线相交

//Voronoi多边形结构体

//构成该Voronoi多边形的边集合

//Voronoi多边形对应的平面点

//网格单元结构体

//网格单元内平面点的个数

//网格单元内平面点集合

//网格单元的边界最下角点和最上角点//网格内Voronoi多边形边个数

//网格内Voronoi边集合

//二叉树存储的网格单元集合

//网格单元

//网格单元的左右(上下)两侧子网格单元

在算法实现时，可以置每个非叶子结点中的BlockSite指针为空，因为实际的Voronoi子图计算都是在叶子结点内进行的，根结点只是为查询检索需要，不必实例化其BlockSite指针。

2 边界点提取与子图合并

2.1 边界点提取

在完成自适应分组后，每个子集均采用扫描线算法生成子Voronoi图，如何合并子图成为该算法的关键环节。在实施子图合并时，位于子图四周的部分点对应的多边形结构会发生局部改变，包括多边形构成边的更新与多边形闭合，姑且将这类点称为边界点，边界点的界定与提取方法将直接影响算法的稳定性。

在生成各组点集的Voronoi图时，无论网格内的点集是按照扫描线从左至右、从右至左、从上至下或从下至上得到，其结果Voronoi图是唯一的。设想将扫描线从无限远处拉回到网格边界线上（此时网格边界线也可看作扫描线），则每个网格对应着4条扫描线，这些扫描线处于向外推进的状态。

如图4所示，图中的铅垂线为两相邻网格的公共边界，若将此边界线看作扫描线，向两侧网格内分别作岸线，左侧岸线由点P1、P2、P3产生的抛物线构成，右侧岸线由点 Q1、Q2、Q3产生的抛物线构成。扫描线两侧的图形欲做合并，若固定左侧，将扫描线向右推进，左侧岸线的左后方不受影响；同样地，若固定右侧，将扫描线向左推进，右侧岸线的右后方也不受影响。因为Voronoi图中每个顶点正是共享此顶点的多边形所在平面点的外接圆的圆心，岸线后方所在多边形顶点及其对应的各边都不会因为Voronoi图的合并发生改变，其原始平面点也不必再提取作为边界点。若上述结论不成立，例如在图中扫描线左侧插入新的一点P'，其不为边界点，但是P3、Q3和P'能够构成空外接圆，而按照扫描线算法理论，满足这一条件的前提是该点P'必须是组成左侧岸线的点，因为岸线一侧的点与扫描线另一侧的点发生圆事件时该点必须为构成岸线的点，故已经排除出构造岸线的平面点不能再次发生圆事件。

图4 网格边界扫描线及其两侧岸线

在图5中，加粗竖线为两网格单元的分界线，加粗折线为两网格单元合并时新加入的 Voronoi多边形边，这些新增加的折线段实现了原网格单元边界处Voronoi多边形的封闭，每条折线段正是边界线两侧某两点之间的垂直平分线。而网格内位于边界附近的一些Voronoi图顶点将因子图合并而舍弃，如图中的顶点O，它是边界点A、B和C的外接圆圆心，在进行子图合并时扫描线右侧的某点与A、B、C构建新的3条垂直平分线，这3条平分线将A、B、C间的原平分线进行了分割，从而顶点O不复存在（它不再是新垂直平分线的交点）。

图5 网格边界Voronoi多边形合并

在算法实现时，针对每条与边界线相交的边，将记录该边是与网格单元4条边界线的哪条边界线相交，根据该信息可以较方便地提取各边界线附近的初始边界点。基于初始边界点，按照岸线理论可建立初始岸线，此岸线并不一定与以边界线为扫描线的最终岸线重合。在网格单元内形成的Voronoi图中，某些平面点生成的多边形虽然闭合，但是该点与边界线构成抛物线可能与初始岸线仍然有相交情形出现，通常出现在与初始边界点共Voronoi边的点中。在检索其他边界点时，可采用以下步骤进行：

1）构造一个队列，将初始边界点逐个加入队列，成为边界点队列，标记每个点已经被判定过；

2）逐个遍历队列中的边界点，提取与该边界点共边的相邻点；

3）遍历这些相邻点，若该相邻点已经判定过，则跳过；否则为该点构造抛物线，计算抛物线与岸线的相交关系，若相交则更新岸线，并将该点加入队列，标记该点已被判定过；

4）当队列中的边界点都被遍历过，则终止判定，队列中的点集就是该条边界线对应的边界点。

上述步骤的关键点在第3步，当某边界点相邻的点都没有能够继续更新岸线，则终止寻找这些相邻点的“二阶”相邻点，即停止对该边界点的外延。因为边界点所在的未闭合多边形组合正好是位于边界点某侧的“第1层”Voronoi多边形，此时需要以这些多边形为基础进行外延，提取后续满足能够更新岸线的新的多边形。

2.2 Voronoi子图合并

子网合并是要找到并插入如图5所示的一条折线，它由两侧边界点的垂直平分线所组成，可通过以下方法实现：在为网格单元生成 Voronoi图的同时，提取每个网格单元的边界点，将边界点作为一组点集并生成Voronoi图；那么，任一网格单元内的边界点将具有两个 Voronoi多边形，一个是网格单元自身生成的，一个则是边界点集生成的。边界点对应的两个多边形的交集即是该点合并后的Voronoi多边形。

尽管边界点在两种子图中的多边形形状不尽相同，但是网格内部边界点与边界点之间的Voronoi边关系基本保持不变。因此，同一边界点对应的两个Voronoi多边形必定有几条边其构成的直线方程相同，或者边的长度位置都未曾发生变化。事实上，合并后的边界点对应的Voronoi多边形正是上述两个多边形区域的交集。如图6所示，图中的水平线为两个点集分组的边界线，两条连续的抛物线链是该边界线对应的两侧岸线。两条岸线之间所夹的一条连续折线正是在进行合并时需要计算得到的。这条折线在为边界点集生成的Voronoi图中可直接得到，如图6中边界点 O在分组内生成的 Voronoi多边形包含FABC，其中FA为射线，AB为线段，BC为射线；而点O在边界点生成的Voronoi图中多边形包含BCDEF。针对这两个未封闭的多边形合并方法较为简单，主要是求取多边形的交集部分并构造新的封闭多边形，对于已经形成的线段可以不用修改，仅仅对射线间进行求交运算即可实现封闭。

图6 分组间Voronoi多边形合并

3 分组并行计算

长期以来，并行计算理论在数值计算及非数值计算领域有了较快的发展，先后提出了多种并行计算模型，如PRAM、BSP、LogP等。基于这些计算模型的常用并行算法主要有两类：一类是SIMD（单指令流多数据流），另一类是MIMD（多指令流多数据流）。前一类并行算法中，各处理机同时处理相同的指令，只是所处理的数据不同，这主要体现在数据处理上的并行性；后一类并行算法中，各处理机处理不同的指令，并可以对不同的数据进行独立操作，处理器之间互不干扰，这是对算法流程自身的一种并行处理。

前人对二维欧式空间平面点集Voronoi图生成的并行算法也进行了相关尝试，如文献[17]为平面上有n个点的点集提供n个处理器，该算法属于一种递归方法：给定一条垂直分界线每次将平面上的点集分为左右两组，各组点个数大约为n/2，并为每个组分配n/2个处理器，然后计算穿越垂直分界线两侧的“等值线”。算法在每执行一次递归时就计算分界线两侧的“等值线”，当递归结束时，合并“等值线”。文献[18]基于对称凸距离函数，提出一种随机并行算法。该方法采用随机采样数据构建Voronoi图，在算法中使用固定数目的处理器。现有基于并行技术的Voronoi图构建算法主要分为两类：一类在构建分组后为每个分组分配一个处理器，另一类为固定处理器个数，分组数量不定。本文采用后一种方式实现并行运算，在现有多核处理器的基础上，为平面点集构建分组。

本文算法中，采用点集自适应分组构建并行计算环境，是一种典型的SIMD算法，每个处理机的工作内容相同，只是各自处理不同的分组数据。由于算法中还涉及到点集分组、边界点提取构建Voronoi图、子Voronoi图合并等环节，这3个环节是前后相继处理的。为此，可以在处理机中确定一台主机，其他处理机作为从机，主机负责点集自适应分组、分组数据向从机分发以及接收处理结果，并在主机上完成子Voronoi图合并，从机只需对接收到的点集构建Voronoi子图并提取组内边界点。具体处理过程如下：

1）主机按照给定的网格参数对平面点集进行自适应分组，假定分为N组；

2）针对M个处理机，主机逐个为每个处理机分配一个分组点集，并即时监听各从机的运行结果；

3）主机监听到某从机运算结束，从机将运算结果发送到主机，若主机上还有点集分组未处理完，则继续为该从机分配一个点集分组；

4）按上述步骤，直到将主机上的点集分组处理完毕；

5）主机根据各个点集分组生成的 Voronoi子图和收集到的边界点，为边界点集生成Voronoi子图；

6）针对上述N+1组Voronoi子图，完成子图合并。

4 测试与分析

本文算法首先对二维平面点集进行自适应分组，然后在各分组内采用扫描线算法构建Voronoi图，最后进行各网格单元子图的合并。算法耗时主要由点集自适应分组、各组点集的Voronoi图构建、边界点提取与Voronoi图构建、子Voronoi图合并4部分构成。为评估各环节的耗时情况，我们进行了一些测试，测试结果如表1所示。

测试结果表明：

1）算法耗时主要集中在Voronoi子图构建环节，与总耗时相比，点集分组、子图合并等所占时间甚少；

2）由于 Fortune扫描线算法的时间复杂度为O(nlogn)，即使不采用并行计算技术，在单处理机环境下采用分组计算策略亦能一定程度上提高算法效率；

3）本文算法针对最耗时的环节（构建Voronoi子图）进行并行化处理，可显著提高算法效率。但需补充说明的是，分组数量并非越多越好，因为它会影响到所提取的边界点数量，最极端的情形下（例如每个点作为 1组），原点集中的点均成为边界点，此时分组策略将失去意义。

表1 算法效率测试结果表

5 结 束 语

基于二维欧式空间平面点集的Voronoi图是Voronoi图研究领域里面最为成熟也是应用最广的一类Voronoi图。前人针对这类Voronoi图的生成给出了数十种算法实现，主要可以归纳为矢量和栅格方法两种，栅格方法由于难以保证其数据精度，限制了Voronoi图的应用场合，而矢量方法在算法时间复杂度上难以突破 nlogn，在遇到数据量较大的情况下，其运算耗时较长，难以满足实际应用。本文借鉴矢量和栅格方法各自的优缺点，提出采用基于二叉树的自适应分组方法，将平面空间点集预先进行点集分组，并采用并行计算技术提升算法效率。本算法以 Fortune的扫描线算法为基础，引入了网格自适应分组方法提升算法运算效率，因为分组间的Voronoi图生成比较独立，它便于在并行计算环境下实现，在数据量较大时，并行环境能有效降低单机环境下算法对内存及磁盘空间的限制。

[1] Ryu J,Park R,Kim D S. Molecular surfaces on proteins via beta shapes [J]. Computer Aided Design,2007,39(12): 1042-1057.

[2] Okabe A,Boots B,Sugihara K,et al. Spatial tessellations: concepts and applications of Voronoi diagrams [M]. Wiley,Chichester,2000: 1-42.

[3] Qian Bo,Zhang Lichao,Shi Yusheng,et al. Voronoi approach to recursive generation of tool path for SLS [J].Computer Aided Drafting,Design and Manufacturing,2008,18(2): 13-20.

[4] Li Yang,Feng Wei,Zhou Huamin. Un-thorough delaunay approach for tetrahedral mesh generation [J].Computer Aided Drafting,Design and Manufacturing,2007,17(2): 82-90.

[5] Li Jin,Donguk K,Lisen M,et al. A sweepline algorithm for Euclidean Voronoi diagrams of circles [J]. Computer Aided Design,2006,38(3):260-272.

[6] Yap C K. An O(n log n) algorithm for the Voronoi diagram of a set of simple curve segments [J]. Discrete& Computational Geometry,1987,(2): 365-393.

[7] Kim D S,Cho Y,Kim D. Euclidean Voronoi diagram of 3D balls and its computation via tracing edges [J].Computer Aided Design,2005,37(13): 1412-1424.

[8] Ohya T. Improvements of the incremental method for the Voronoi diagram with computational comparision of various algorithms [J]. Journal of Operation&Research Sociaty,1984,27(4): 306-336.

[9] Held M,Huber S. Topology-oriented incremental computation of Voronoi diagrams of circular arcs and straight line segmengts [J]. Computer Aided Design,2009,41(5): 327-338.

[10] Fortune S. A sweepline algorithm for Voronoi diagrams [J]. Algorithmica,1987,(2): 153-174.

[11] Shamos M I,Hoey D. Closest-point problems[C]//Proceedings of the 16th Annual Symposium on the Fundations of Computer Science,1975: 151-162.

[12] Oishi Y,Sugihara K. Topology-oriented divideand-conquer algorithm for Voronoi diagrams [J].Graphic Models and Image Procedings,1995,57(4):303-314.

[13] Chew L P,Drysedale R L. Voronoi diagrams based on convex distance functions[C]//Proceedings of the Symposium on Computational Geometry,Baltimore,1985: 235-244.

[14] Mark D M. Recursive algorithm for determination of proximal ( thiessen ) polygons in any metric space [J].Geogr. Anal. 1987,19(3): 264-272.

[15] Schwarzkopf O. Parallel computation of discrete Voronoi diagrams[C]// Tech. Rep. Fachbereich Mathematik,Freie Universitat,Berlin,1988: 193-204.

[16] Schueller A. A nearest neighbor sweep circle algorithm for computing discrect voronoi tessellations [J]. Journal of Mathmetical Anaysis and Applications,2007,336(2): 1018-1025.

[17] Cole R,Goodrich M T,et al. A nearly optimal deterministic paranell Voronoi diagram algorithm [J].Algorithmica,1996,16: 569-617.

[18] Ulrich K. A randomized parallel algorithm for Voronoi diagrams based on symmetric convex distance functions [J]. Discrete Applied Mathematics,2001,109(1-2): 177-196.