有效的混合圆弧扫描转换算法

张胜男， 牛连强， 陈 欣

（1. 沈阳工业大学信息科学与工程学院，辽宁 沈阳 110870；2. 沈阳工业大学理学院，辽宁 沈阳 110870）

图形基元的生成算法对整个图形系统的效率和质量具有重要影响。因此，从20世纪70年代起，这些基元的光栅转换算法的研究就已开始[1]，至今仍受到关注[2-4]。目前，直线的光栅转换算法已得到了充分的研究，并发展了2步算法、多步算法、行程算法以及多级行程算法等[2,5-7]，利用很少的几次基本运算即可绘制多个像素。但由于圆弧等曲线的非线性性，其进行光栅转换算法的设计远比处理直线复杂，进展也非常缓慢。

作为经典圆弧绘制算法，Bresenham算法[8]和中点法[9]分别采用两点的距离平方差和中点误差作为决策参数，确定每次每步时的坐标位置，算法简单，容易实现。文献[10]提出了基于中点法的快速算法，该算法先将中点法的迭代关系除以系数 2，再利用奇、偶次迭代来分别处理关系式中的常数1/2，从而消除了系数2所带来的位移运算。本文作者于文献[11]提出了一种直接利用残差实现的另一种有别于前述两种算法的基本圆弧生成算法。由于这些算法的共同点是每步选择一个像素，故被称为基于像素（pixel-based）的算法。

为了提高圆弧的生成速度，目前的研究工作主要集中在以下两个方面：

1）尽量减少每次步进消耗的运算次数；

2）尽量减少输出(I/O)的次数。

很难从理论上说明，每次步进至少需要多少次运算，但由于单步选择像素法的运算量已经难以减小，改进的目标将是多步法。由于现今的硬件设备输出多点像素时的位模式设置时间与输出一个像素的位模式设置时间接近，因此，减少I/O输出次数可以有效地提高绘制效率，这是行程算法的出发点。不过，当圆的半径确定时，行程法所减少的运算量也是确定的。

文献[12-13]首先提出了一个每次步进可绘制两个像素的2步骤算法，该算法利用对连续两点中点的位置关系的预先估计进行判定，以舍弃中间点的数学运算。文献[4]采取重新定义决策参数的方法实现了一种2点步进算法，使每点的运算量达到3.8左右。

文献[14]提出了一个基于水平行程的圆弧的光栅转换算法（记为HCL算法）。HCL算法的主要思想是将 45° ～90°之间的圆弧视为由水平行程组成，因为同一个行程上的像素的y坐标是相同的，故可以根据y-0.5 ～y+0.5的y坐标变化范围确定行程长度的迭代关系，进而求出行程长度并一次性输出这些像素。根据文献[13]的测试，这种算法的圆弧光栅转换效率比传统的单点算法高 1.36倍（对 1≤radius≤128）。

经过比较，我们认为目前最快的圆弧绘制算法是由Yao and Rokne提出的一种混合算法[15-16]。该算法是在HCL算法的基础上结合2点步进实现的。具体地说，Yao-Rokne算法对45° ～90°之间的圆弧的性质做了更细致的分析，并以“y=2x”为界将其划分为2部分。第1部分采用类似HCL算法的迭代公式计算出水平行程的长度，再一次性输出这些行程，但每次循环的增量为 2。由于第2部分的水平行程长度为1或2，该算法采用中点法迭代并输出每个像素。很明显，YR算法具有行程算法的特征，且水平行程的计算速度快，因此，整体圆弧绘制速度有了明显提高。本文作者在文献[17]中提出了一种利用基本迭代关系构造的简单行程算法。

Bresenham算法和中点法一直被认为是经典的算法，其中的重要原因之一是简单性，包括思想简单、格式推导简单和仅使用的简单运算。不过，虽然改进后的HCL算法和YR算法不同程度地提高了绘制效率，但这些结果的推导和理解困难，且引入了开方、乘法等复杂的运算。

本文提出了一种利用中点法技术重新构造迭代关系而得到的2点步进与行程计算、模式分析相结合的混合算法。新算法对水平行程长度大于2的部分和水平行程长度小于2的部分单独处理，但每次迭代几乎都能产生2个（或3个）像素。新算法仅通过推广中点法实现，理论推导容易，且消除了YR算法中的乘法，仅使用简单运算实现，其效率高于现有的其它算法。

在以下的讨论中，假定圆弧的圆心在坐标原点，圆弧半径r为整数。由于圆的对称性，仅研究 45° ～90°的圆弧绘制，其他 7个 1/8圆弧可由对称性得到。约定在目标像素与圆弧真实值的误差为0.5时，取下方像素。

1 相关的工作分析

1.1 WR算法

Wu和Rokne在文献[9]中提出了一个双步圆生成算法（记为WR算法），如图1所示。设当前点为(x,y)，该算法判断圆弧是在(x+2,y)与(x+2,y-1)之间的中点（记为中点 2）之上还是之下，或是在(x+2,y-1)与(x+2,y-2)之间的中点（记为中点3）之上还是之下。

1）若是在中点 2之上，则画两点(x+1,y)和(x+2,y)；

2）若是在中点 3之下，则画另外两点(x+1,y-1)和(x+2,y-2)，并转到第2个1/16圆弧生成部分；

3）如果圆弧在两个中点之间，则不加区分地画 3 点(x+1,y)、(x+1,y-1)和(x+2,y-1)。

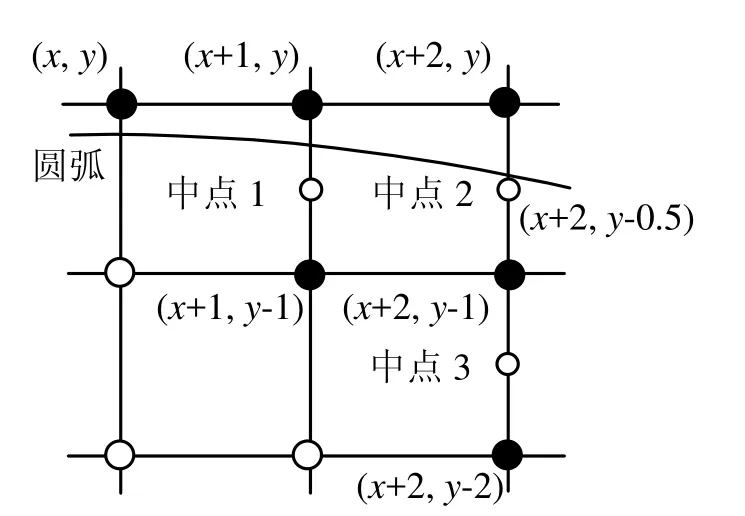
图1 圆弧经过的位置

上述方法可以有效地减少计算量。不过，在绘制3点时，(x+1,y) 和(x+1,y-1)中的一个像素到圆弧的距离必然要大于0.5个像素单位（除非圆弧恰好通过两像素中点的特殊情况），甚至这个误差有可能大到接近一个像素单位1，这与生成曲线的最佳逼近（小于等于0.5个像素单位）的原则不符。

1.2 HCL算法

Hsu、Chow和Liu提出的HCL算法基于这样的观察：光栅转换圆弧可以被视为由y坐标相同的水平线段（称为行程）所组成。当i≥1时，第i段水平行程的y坐标为yi=r-i+0.5。若假设此行程的最大x坐标为Si，则有

(x+1)2=x2+2x+1。

对于水平行程长度较大的情况，HCL算法可以在一定程度上提高绘制效率。

1.3 YR算法

Yao和Rokne在HCL算法的基础上对圆弧的特性进行了更仔细的研究，并建立了如下结论：

定理1设D(x,y)为如图2所示圆弧上满足y=2x的点，该点将图中位于45° ～90°的圆弧分为C1和C2两段，则有

如果水平位移 Li完全包含于 C1，则该水平位移的长度 li≥ 2 ；

如果水平位移Li完全包含于C2，则该水平位移的长度 li≤ 2 。

图2 由点D将八分圆弧划分成两个部分

证明参见文献[15]。

利用上述性质，YR算法只对C1部分计算水平行程，其迭代关系与 HCL算法基本相同，而对C2部分仍采用传统的中点法。对C1部分采用的迭代形式如下

如果采用4作为增量，则x可以每次循环步进2点，使得计算量得到减少。

注意到上述迭代中没有累计误差，在转入C2部分后，YR算法需要按如下公式给出初始的误差

这里引入了2次乘法，增加了算法的复杂性。

2 水平行程的特性

在YR算法中，为了直接计算行程的长度，圆弧被小心地划分为两部分。但是，定理1中满足条件“y=2x”的点D很难简单精确地确定。此外，直接对迭代并计算出 Si的代价也很高，且不能得到C2部分起始点的误差。

事实上，如果直接采用误差来控制每次迭代，则并不需要精确地区分C1和C2。为此，本节建立一个用于描述相邻水平行程之间关系的结果。

定理2在光栅圆弧中，除了第1个水平行程外，若 45° ～90°圆弧的第 i段水平行程长度为li(i≥1)，则第i+1段的水平行程长度li+1≤li+1。

证 明记第 i段水平行程的起点(,yi)处圆弧与上0.5分度线的距离为 δ ()，圆弧在点(,yi)与(,yi+1)之间 y 方向变化量为 Δ ()，参见图3。则有

图3 相邻的两个行程的长度比较

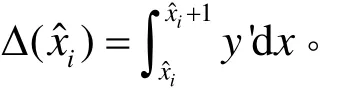
证毕。

定理2对复杂模式分析非常有效，如果已知当前行程长度，且下一个行程长度大于当前行程长度，则无须判断可直接得到该长度。

推 论在定理2的假设下，若第i段水平行程长度为则对所有 j >i，有 lj≤li+1。

3 混合行程算法

根据定理2，不需要关心C1、C2部分的划分点D的准确位置，代之以检测第1条长度为1的水平行程。这是因为如果在绘制过程中遇到一条长度为1的水平行程L，则其后的水平行程的长度只能是1或2，而在L之前的行程长度都大于或等于2。因此，可以对L之前和之后的光栅圆弧分别采用不同的处理方法。显然，只要能够以较快的方式得到行程长度，就可以消除YR算法中的2x运算。

3.1 最简单的行程算法

传统的中点法依据中点与真实曲线的相对位置关系确定被选择的像素，若用D表示决策参数，则有如下结论：

1）初始决策参数满足D0=1-r；

2）假设当前被选择的点是P(xP,yP)，决策参数为DP，则下一步可能的选择为E和SE，分别对应着水平步进和对角步进，如图4所示。

图4 中点法的步进点选择

如果DP<0，则选择E，且有

DP+1=DP+ΔE=DP+2xP+3；

如果DP≥0，则选择SE，且有

DP+1=DP+ΔSE=DP+2(xP-yP)+5。

上述算法可以被容易地改写成行程算法：

在需要分别处理C1和C2部分时，可将最后的步骤修改为：

if(行程长度>1) goto REPEAT;

这种改写不需要任何准备工作。如果采用差分，可以进一步减少运算量。

尽管算法1和算法2非常简单，但他们的效率都不低于HCL算法以及文献[14]提出的算法1的效率，且不需要任何复杂的运算。以下我们继续讨论建立在上述算法之上的多点步进算法。

3.2 2点步进的水平行程处理

观察图 5，仍假设当前被选择的点是 P(xP,yP)，并记

ΔE=2xP+3，

ΔE代表了水平步进2点时的中点（参考点）处应该累加的误差。

1）向前步进2点

如果 DP+ΔE≤0，那么，下一次选择的点为P+2，更新决策参数为

DP+2=DP+2xP+3+2(xP+1)+3=DP+4xP+2，

ΔE=ΔE+4。

图5 水平方向的2点步进

2）向前步进少于2点

如果 DP+ΔE≥0，那么，下一次选择的点应为SE1或SE2。于是，继续判定：

若 DP<0，则水平步进 1点，再对角步进 1点，即选择P+1和SE2，有

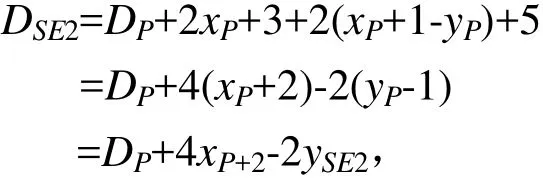
3）行程长度确定

算法中的一项重要工作是判别行程长度，并在遇到长度为1的行程时结束算法。不过，直接对长度进行判别需要附加的运算，因此，本文采取了如下方法：每次的行程计算时，将第1次对条件“DP+ΔE≤0”的判定从循环中独立。如果该条件为true，再判定条件“DP>0”成立，若此条件成立，则算法结束。这样，仅在已知行程长度不超过2时判断其行程长度是否为1。

3.3 沿对角方向2点步进

由中点法的步进规则可知，每次沿对角方向步进消耗的运算量是比较大的。有效地提高 C2部分的绘制效率对整个算法的效率影响很大。

观察图6，对于当前被选择的点P(xP,yP)，记

则ΔSE是沿对角方向步进两点时的中点（参考点）处应累加的误差。

于是，初始时的决策参数为DP=DP-1-ΔSE – 4。

1）沿水平和对角各步进1点

如果DP<0，应选择点P1和P3，有

2）沿对角、水平和对角方向各步进1点如果DP≥0，应首先沿对角方向步进到点P2，并判别：

如果 DP+ΔSE<0，继续选择 P3和 P5点，更新决策参数为

DP5=DP+2(ΔSE+xP5)+5，

ΔSE=ΔSE+10。

如果DP+ΔSE≥0，应选择点P4，有

DP4=DP+2ΔSE+4，

ΔSE=ΔSE+8。

为了避免“DP+ΔE”和“DP+ΔSE”中的加法运算，可以将ΔE和ΔSE取负，并将对D的更新中的ΔE和ΔSE项的符号取反。

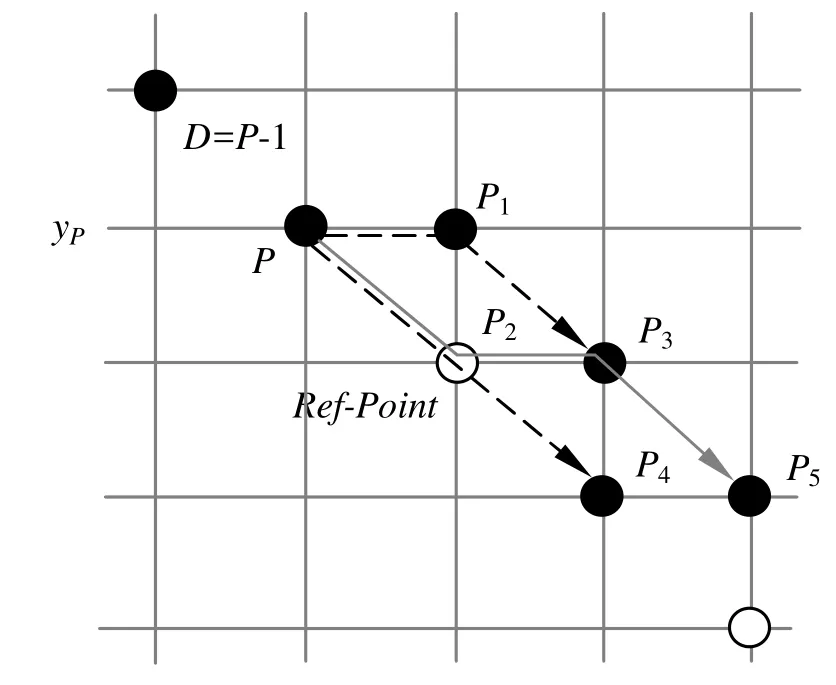
图6 对角方向的2点步进

3.4 算法描述

算法3几乎每次循环都可以步进2点或3点。在C2部分的连续绘制y坐标相同的2点可以采用画线命令一次输出。

4 进一步的改进措施

通常，对圆弧的光栅转换算法的改进在绘制半径较大的圆时更有意义，而对半径较小的圆，基本生成方法是优先的选择。此外，我们认为对算法的改进主要有两个方向：

1）将2点步进改为n点步进；

2）进一步详细分解模式，根据不同模式采取不同的处理方法。

4.1 行程模式的差异

光栅圆弧上不同部分的行程模式差异很大，表1统计了100≤r≤1000时不同行程长度所占有的比例和平均像素数，由此可说明改善哪些部分的绘制算法对整体生成算法的效率影响较大。

根据表1可将1/8圆弧粗略划分为像素个数接近的3个部分，即水平行程长度为5以上的部分、水平行程长度为2 ～4的部分以及行程长度为1 ～2的部分，而行程为2 ～3的部分接近行程长度为3 ～4的部分的2倍。

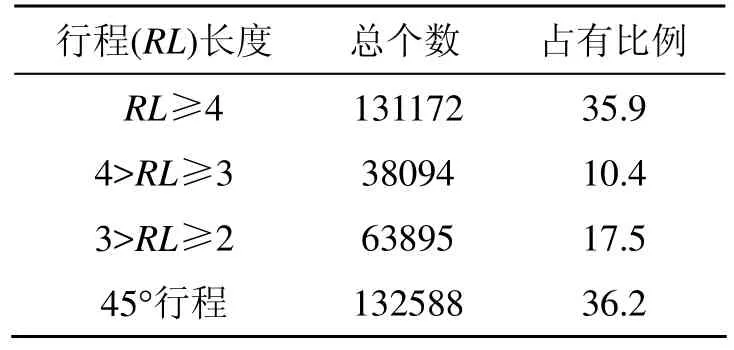
表1 圆弧不同区段的像素个数统计(100≤r≤1000)

4.2 4点步进加速

很明显，如果对整体1/8圆弧每次步进前移4点，算法在水平行程结束时需要较多的判断，行程长度为2 ～4部分的效率会很低，实际测试也说明了这一点。因此，我们考虑仅在算法2之前增加4点步进作为一种加速措施。如果行程长度小于4，则立即转入算法3。

我们实际测试了4点步进算法，其效率提高的幅度并不明显。

4.3 单独处理特殊的模式

根据像素模式的不同分别采用不同的绘制策略是提高绘制速度的另一种途径。例如，由表1可知，行程长度为2 ～3的部分占有较大的比重，提高这部分圆弧的绘制绘制速度对整体算法的效率将会产生一定的影响。

由定理2，在第1次绘制一个长度为2的水平行程后，和直到遇到第一个行程长度为1的行程为止，中间的行程长度只能是2或3。因此，可以按下述方法绘制此区间的圆弧：

利用上述部分算法替换掉算法3中的如下语句就得到了一个完整的加速算法

在特别强调效率时，还可以用同样的方法绘制行程长度为3 ～4的部分。

5 算法分析

虽然可以在理论上对算法所采用的各种运算量进行分析，但需要进行较多的估计和假设。例如，对于图7，容易说明其中的几种长度h1,h2,w1,w2，并由这些长度确定各种步进的点数，进而将它们与运算次数相乘后求和即可得出各种运算的总次数。但是，对行程长度为2起始至分点D之间的长度h3和w3很难准确计算。同时，在采用单步法时，可以比较准确地计算出x方向和y方向步进发生的时刻，但在采取2点步进时，就需要做过多粗略的估计[14]，其结果并不准确。

考虑到实际运行程序所得到的时间受多种因素影响，且不同的算法采用的运算也有差异。因此，我们通过实际跟踪每次运算来得到各种运算的精确次数，并遵循下述原则：

1）统计的运算包括加法、位移、符号判定和逻辑运算，分别记为Na,Ns,Nt和Nc。

2）不包括对x和y的坐标变化的计算。

3）乘2的幂运算被视为位移运算。

4）由于在圆的半径较小时，一般改进后的算法并没有什么优势，故测试只对 32≤r≤1024的圆弧进行（平均值）。

图7 不同区域的长度

实际测试算法3的结果及YR算法（原文的理论分析结果和实际测试结果）和单点算法的理论分析结果见表2。

表2 不同运算的执行次数比较(33≤r≤1024)

表2对YR算法的测试未包括进入C2部分之前的初始化工作（2次乘法和其他运算）。很明显，算法 3比单点算法及 YR算法消耗更少的运算量。测试也说明，由于假设较多，文献[14]的理论分析结果的误差是较大的。

为了对各种算法有更全面的比较，我们视所有基本运算为1个时间单位，一次乘法为12个时间单位，实际测试并得出了几种算法实际消耗的平均运算次数（见表3）以及每点平均消耗的基本运算次数（见表4）。图8显示了YR算法、本文算法3与中点法的运算量之比。

因为绘制像素的时间与实际硬件有关，本文对I/O次数不进行比较（行程法的I/O次数基本相同）。此外，考虑到HCL算法包含开方、乘法等复杂运算，效率明显低于YR算法，故仅提供了与YR算法3以及经典中点法之间的比较。

表3和表4表明，本文提出的4种算法都具有比目前已存在算法更高的效率。其中，算法2仅由中点法做简单改造，其效率略优于YR算法，但该算法极为简单。算法3代码长度与YR算法接近，但其消耗的运算量约为YR算法的80%。步进1点平均消耗的基本运算约为3次，仅比单点直线生成算法的每次步进多消耗1次运算。算法 4和算法 5的代码较长，消耗的运算量约为YR算法的75%。如果将算法4和算法5的加速技术与算法3融合，每点平均运算量可达到2.5左右，其缺点是代码过长。与HSL算法和YR算法相比，本文算法2和算法3无需任何复杂推导，结构简单，没有任何复杂的运算，运算量和程序代码量较小，具有明显的优势。

图8 YR算法及本文算法3与中点法的运算量之比

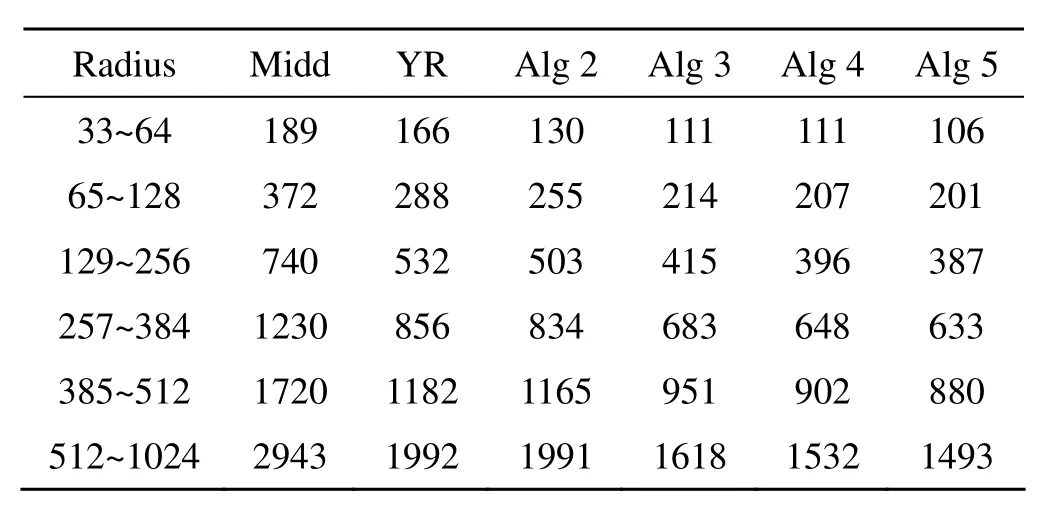
表3 计算量比较

表4 绘制每点平均计算量比较

由于行程法可以有效地减少像素输出的时间消耗，一个很自然的想法就是先计算出组成圆弧的所有行程的长度，再绘制这些行程，这是HSL算法和YR算法的出发点。但是，计算行程长度本身要求解一个非线性方程，求解方法设计、理解困难，只能采取迭代法来避免引入复杂运算，而这种迭代也需要逐点进行，并不会比直接对决策参数的迭代减少运算量。同时，当绘制区域变化时，其初始误差需要特殊计算，不可避免地要引入乘法。类似地，这种方式也难以对不同的区域采取特殊的有效策略。

试验也表明，超过2步的多步法很难得到更大的优势。对于非线性曲线，以较低的代价直接计算出水平行程的长度是困难的，在强调绘制速度时，利用决策参数递推并结合对复杂模式的细致分析是更好的策略。

6 结 束 语

本文利用2点步进重新构造了传统中点算法的决策参数，提出了一种快速生成圆弧的混合行程算法。该算法几乎每次循环都可步进2点，少量循环步进1点或3点，且水平行程可以一次性计算和输出。利用加速措施得到的几种新算法可以分别以平均每点 2.7 ～3.7次基本运算的计算量完成整个圆弧生成，效率明显优于现有的其它算法。由于新算法仅采用中点算法的决策参数进行误差控制，思想、推导简单，需要更少的辅助手段，且有利于用更优的策略替代算法中的任何部分，进而得到更高的效率。此外，新算法没有引入任何复杂运算，如乘法、开方等，有利于硬件实现，且算法的思想可以推广到椭圆、抛物线等典型曲线的绘制。

[1] Bresenham J E. Algorithm for computer control of a digital Plotter [J]. IBM System Journal,1965,4(1):25-30.

[2] Boyer V,Bourdin J J. Auto-adaptive step straight-line algorithm [J]. IEEE Computer Graphics and Applications,2000,20(5): 67-69.

[3] 程 锦,陆国栋,谭建荣. 一种快速圆弧绘制算法[J].软件学报,2002,13(12): 2275-2280.

[4] 刘勇奎,石教英. 圆的像素级生成及反走样算法[J].计算机辅助设计与图形学学报,2005,17(1): 34-41.

[5] Gill G W. N-step incremental straight line algorithms [J].IEEE Computer Graphics and Applications,1994,14(3): 66-72.

[6] Fung K Y,Nicholl T M,Dewdney A K. A run-length slice line drawing algorithm without division operations [J]. EUROGRAPHICS '92,1992,11(3):267-277.

[7] Boyer V,Bourdin J J. Fast lines: a span by span method [J]. Computer Graphics Forum,1999,18(3):377-384.

[8] Bresenham J E. A linear algorithm for incremental digital display of circular arcs [J]. Communications of the Association for Computing Machinery [J]. 1977,20(2): 100-106.

[9] Foley J D,Dam A V,Feiner S K,et al. Computer graphics: principles and practice [M]. Addison-Wesley Publishing Company,Reading Massachusetts,1990:89-172.

[10] Kuzmin Y P. An efficient circle-drawing algorithm [J].Computer Graphics Forum,1990,9(4): 333-336.

[11] 牛连强,冯海文,吴 澎. 利用残差控制的快速圆弧生成与反走样算法[J]. 计算机辅助设计与图形学学报,2011,23(2): 232-239.

[12] Wu X,Rokne J. Double-step incremental generation of lines and circles [J]. Computer Vision Graphics,and Image Processing,1987,37(3): 331-344.

[13] Wu X,Rokne J. Double-step generation of ellipses [J].IEEE Computer Graphics and Applications,1989,9(3): 56-69.

[14] Hsu S Y,Chow L R,Liu C H. A new approach for the generation of circles [J]. Computer Graphics Forum [J]. 1993,12(2): 105-109.

[15] Yao C,Rokne J G. Hybrid scan-conversion of circles [J].IEEE Transactions on Visualization and Computer Graphics,1995,1(4): 311-318.

[16] Yao C,Rokne J G. Run-length slice algorithms for the scan-conversion of ellipses [J]. Computer &Graphics,1998,22(4): 463-477.

[17] 牛连强,薛 瑾,朱天翔. 快速绘制圆弧的行程算法[J]. 沈阳工业大学学报,2010,32(4): 411-416.