正轴测投影反求建模研究

林大钧

（华东理工大学机械与动力工程学院，上海 200237）

设计从三维开始是现代工程设计的一个重要标志。传统多面视图成图形式缺乏立体感和直观性，对人的空间思维有一定的抑制性。随着计算机图形技术的发展，在工程设计中三维建模将起到越来越重要的作用。然而在设计初始阶段，一种有立体感的二维图形非常适合于描述人脑对形体的原始构思，这种图形就是轴测投影图。人处于三维空间，看到的以及触摸到的都是三维的物体，头脑中存储的也是立体图像，为了使人在初始设计和交流产品形状时无障碍，最好的方法是将头脑中进行的三维思考用有立体感的正轴测投影图加以表达。但是，由于正轴测投影图绘制不便，并且受一个正投影图不能唯一地确定物体的空间形状和大小这一基本概念的约束，正轴测投影图一直以来都被当作参考图形而处于从属地位。通过对正轴测投影理论的深入研究，并结合计算机图形技术，认为可以通过一个正轴测投影图反求物体的形状和大小[1]。这一发现，使我们认识到一个改变传统设计表达方法的契机已经来临。

1 应用投影变换方法获得正轴测投影图

任何一种投影体系都必须具有投影光线、投影面和物体3个基本要素。轴测投影体系也不例外，当投影光线与投影面垂直时，所建立起来的投影体系称为正轴测投影体系。根据这一定义，可利用投影变换的方法获得正轴测投影图。由图1(a)可知物体在 V、H投影面上的投影没有直观性，当改变投影方向，如图 1(b)所示，观察者沿投影方向S看物体时，在P投影面上（S⊥P）的投影就有直观性，可以帮助我们理解该物体的立体形状。为了在投影面上画出这个有立体感的图形，只须将投射线S变换成投影面的垂直线，物体也跟着一起变换，在新投影面上就可得到有立体感的图形了，如图2所示。图3是转正后的图形，在此图形中可量取轴间角，根据轴间角可以计算轴向伸缩系数和投影方向。

图1 物体的投影图

图2 由投影变换获得物体的正轴测投影

图3 转正后的正轴测投影

2 轴向伸缩系数与轴间角的数学关系[2]

根据投影变换的方法可以分析轴向伸缩系数与轴间角之间的关系，把物体上的坐标系OIJK的原点置于x轴并取为单位长），使投影方向过原点O，设S在空间坐标系中的位置由φ，β角确定，如图4所示。

第 1次投影变换将 S变为正平线（应有x1//S ）。为简单起见使 x1轴与 S的水平投影 s重合，并过原点O，物体上坐标系OIJK也随之变换为 O1I1J1K1。第2次变换将投影方向变换为铅垂线，此时新投影轴x2必垂直于 O1' S1'，其与x1轴交于O2，设x1轴与x2轴的夹角为θ，由图4可知θ、φ、β之间有关系

图4 投射方向、轴间角、轴向伸缩系数的关系

物体上坐标系 O1I1J1K1也随之变换为O2I2J2K2。注意，x2轴的方向与 O1'S1'垂直，但x2轴的位置不是唯一的，图中位置是为图形清晰起见而设，而为使寻求投影方向，伸缩系数，轴间角之间的关系容易起见，可将 x2轴平移，使O1与O2重合。这时由图4可得I、J、K 3点在X2O2Y2坐标面中的坐标。

由于 x2O2y2即为正轴测投影面，而O2i2、O2j2、O2k2即为轴测轴，因此可得伸缩系数为

由式（4）即可得

式（5）表明正轴测投影 3个轴向伸缩系数平方和恒等于2。而由图4可知，轴间角为

由于θ为β，φ的函数，故伸缩系数，轴间角与投影方向之间的关系即为式（4），式（5），式（6）。根据这组公式就能根据轴间角计算出投射线的方向和各轴向伸缩系数，这是反求的重要步骤，因为在已知的正轴测图上，轴间角可从图上量取，是已知信息，根据轴间角反求轴向伸缩系数和投射线方向，再结合将一般位置直线变换为投影面垂直线的步骤，建立正轴测投影的数学模型。

3 正轴测投影数学模型的建立

如上所述，要由计算机获得有立体感的投影图，关键要建立将一般位置直线变换为投影面垂直线的数学模型[3]。设α0、β0为确定直线空间方位的已知参数，如图5所示。

图5 一般位置直线的投影变换

根据投影变换的作图顺序，在相应的投影体系中建立一个坐标系与之对应。如图 5中与oxyz对应；对应；与 o2x2y2z2对应。且使oxyz与 o1x1y1z1共原点，即o、o1两点重合在x轴上，而坐标系 o2x2y2z2的原点建立在x1轴上，o2、o1相距为L。由投影变换的方法可知L的长度可以任意选取而对解题结果并无影响。将直线AB进行第2次变换时，投影体系与新投影体系的相对位置取决于 H2面和V1面的交线x2轴的位置，也即由β角确定。由此知直线AB经2次投影变换后的投影取决于β0和β角。在将一般位置直线变换为投影面的垂直线的系统中，如有一点 I ( xi,yi,zi)随直线AB一起变换，则I点经一次投影变换后其在 o1x1y1z1坐标系中的坐标为

经第 2次投影变换后其在 o2x2y2z2坐标系中的坐标为

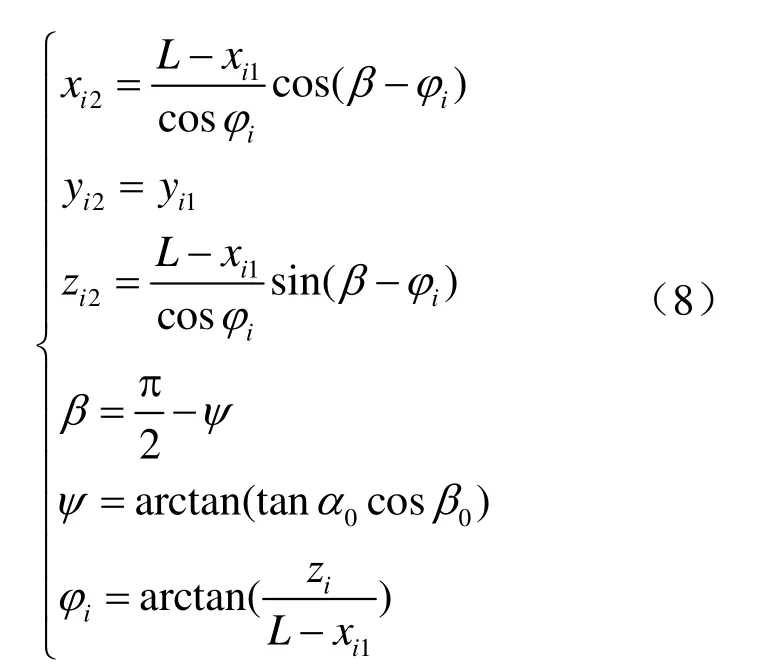
式（7）、式（8）即为一般位置直线变换为投影面垂直线的数学表达式，也是正轴测投影的数学模型。

4 正轴测投影反求建模的研究

4.1 反求数学模型的基本框架

由图2可知，在选定观察方向下经过投影变换得到有立体感的投影实际上就是物体的正轴测投影图，所建立的数学式（7）、式（8）也就是画物体正轴测投影的数学模型[4]。

由式（7）、式（8）并参考图 5可得物体上任意一点 I ( xi,yi,zi)的反求数学模型用式（9）、式（10）、式（11）反求I点的原始坐标时还需要确定zi2或φi。

4.2 一般伸缩系数

由图4可知，在立方体正轴测投影上，各边的投影长为已知，当反求出轴向伸缩系数后即可得各边实长，对于轴上的线，或者与轴平行的线都可以反求实长，但对于与轴倾斜的线，比如图4中的其实长就不能直接反求得到。假设与其实长之比为s称为一般伸缩系数，图4中，按定义一般伸缩系数s为

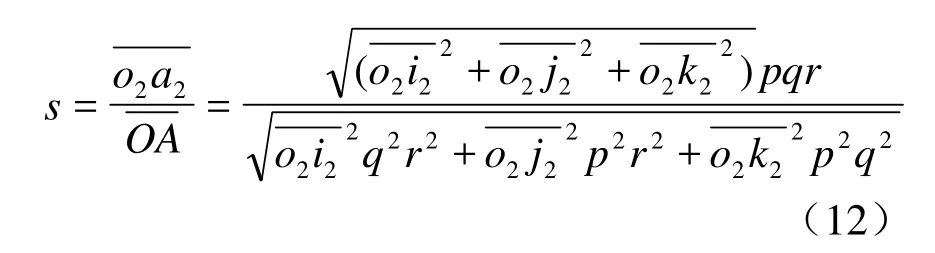
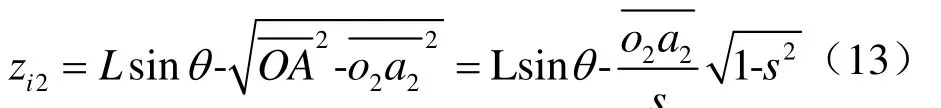
结合式（9）、式（10）、式（11）、式（12）、式（13）即可反求建模。

4.3 实 例

为根据任意观察方向下的正轴测投影图反求物体大小，以图1所示物体为例，先画出所设方向下的正轴测投影，如图3所示，再根据正轴测投影图形反求物体的三维实形[5]。利用式(7)、式(8)编制绘图程序，并运行得到物体正轴测投影图形的各点坐标及轴测投影图，如图 6(a)、(b)所示。利用式(1) ～式(6)编程，计算观察方向为时的轴向伸缩系数和轴间角，结果如图6(c)所示。

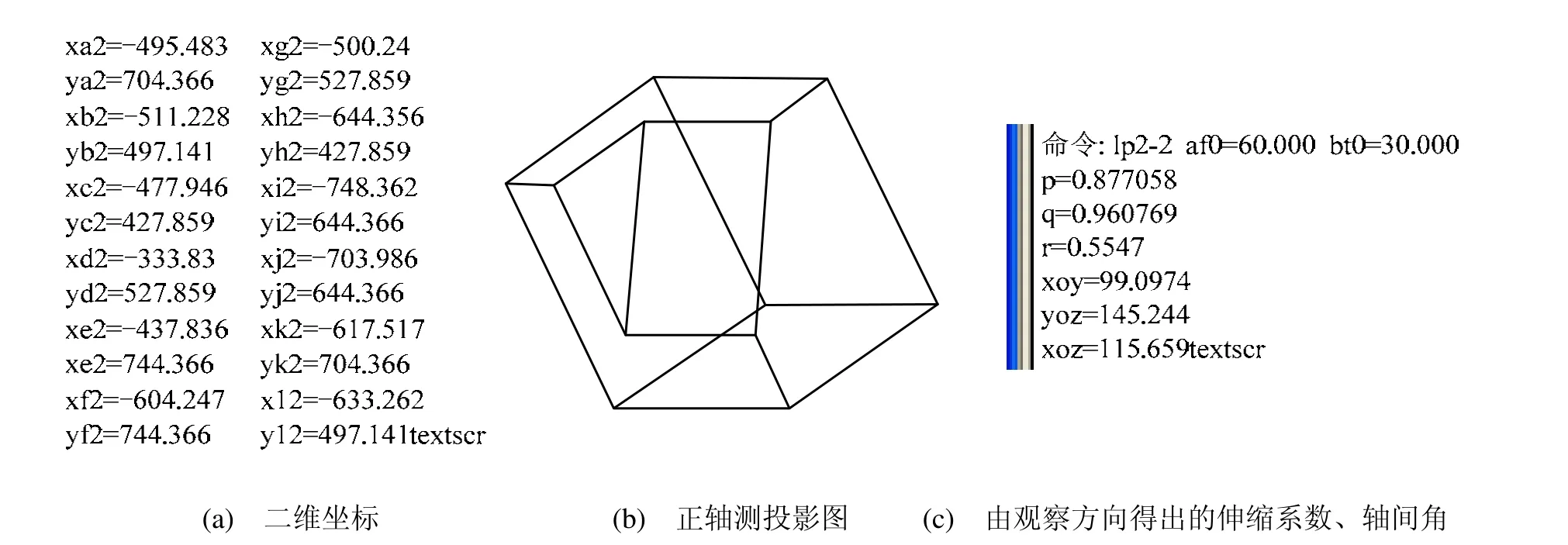
图6 正轴测投影图二维坐标与由观察方向得出的伸缩系数、轴间角

根据正轴测投影反求物体真实形状的数学式(9) ～式(11)，编程计算并打印出投影角与轴向伸缩系数，如图7所示。应用图6(a)中的二维坐标，根据式(9)～式(13)编程反求三维点坐标，并绘制物体的三维图形如图8所示。

图7 反求得出的投影角与轴向伸缩系数

图8 物体的三维图形

由图6(c)可知，反求所得的轴间角、轴向伸缩系数、投影方向与原始条件是一致的。由图8(a)中的各点坐标可计算图1(a)所示尺寸[6]。

如忽略不计计算误差，可见反求结果与原尺寸相同。图8(b)所示是物体的三维线框图，可以通过旋转、移动获得各个方向的图形。本例是为了说明反求的正确性，给出了物体的主俯视图和尺寸。如果一开始就用轴测投影图进行设计，就须先根据轴间角反求出β、θ，再反求出φ角，然后才能按照上面的反求步骤求得实际尺寸，造型后生成二维工程图。

5 结 论

到目前为止，尚未见有将正轴测投影反求建模的过程进行系统的研究，论文通过投影变换与一般伸缩系数的研究建立了根据正轴测投影反求实际尺寸的方法，为初始设计着力于产品形状的构思，而不是拘泥于软件的应用提供了途径。

[1] [苏]包太兹,米列斯库. 轴测投影理论与应用[M].周积义译. 北京: 机械工业出版社,1988: 1-6.

[2] 徐宏文. 轴测投影[M]. 天津: 天津大学出版社,2006: 4-12.

[3] 杨 戈. 关于AutoCAD中的轴测投影[J]. 河北工业大学成人教育学院学报,2007,(4): 46-50.

[4] 朱育万,钱承鉴. 阴影与透视[M]. 北京: 高等教育出版社,1993: 102-113.

[5] 吴永进,林美樱. AutoCAD程序设计魔法书[M]. 北京: 中国铁道出版社,2004: 4-7.

[6] Zhan Yibin,Lin Dajun,Aa Qi. Slicing method for reverse engineering based on image mosaic [J].CADDM,2008,18(2): 33-38.