格网划分的双策略跟踪多边形裁剪算法

汪荣峰， 廖学军

（装备学院航天指挥系，北京 101416）

1 相关研究

不要求裁剪多边形为矩形或凸多边形的裁剪算法主要有3类：第1类是建立在比较完备的数学形式之上的算法，如Rivero等[1]和Peng等[2]提出的算法，其优点是理论基础完备，无需考虑特殊情况、鲁棒性好，缺点是算法较为复杂且效率提升困难；第2类算法将交点分割后边分类跟踪形成子区域，通过子区域运算实现多边形布尔运算，如Schutte[3]、Leonov-Nikitin[4]、朱雅音[5]等算法；第3类在Weiler算法[6]基础上得到，将交点分类为进点和出点，进行跟踪得到输出多边形，如 Vatti[7]、Greiner-Hormann[8]、刘勇奎[9]等算法，其原理简单、易于实现，效率较高，本文提出算法也属于此类。

第3类算法的研究集中在3个方面：

1）数据结构设计。Weiler 算法使用树形数据结构，Vatti 算法和 Greiner-Hormann 算法使用双线性链表数据结构，刘勇奎算法采用单链表数据结构。

2）特殊情况处理。需处理的特殊情况是交于顶点和边重合等情况。文献[7]和文献[9]采用对顶点进行微小移动的方法，这对于屏幕绘制等有效，但需精确结果时不适用；鲍虎军[10]根据多边形边界内法向来对交点进行完备分类；刘勇奎[11]将特殊情况分解成各种子情况分别进行处理，通过在链表上增加或减少交点来保持进点出点交替出现。

3）求交效率优化。裁剪算法中最为耗时的是求交点，在不进行任何优化的情况下其时间复杂度为 O(nm)。文献[11]提出了斜率法来优化两边之间的求交运算，对每个点需要执行一次除法；文献[10]提出了应用错切变换处理边求交问题，进一步减少了求交所需运算量；在针对两条边的求交运算上，这两种方法基本已经达到最优，但是就多边形裁剪而言，并没有减少总的求交次数。文献[8]在边求交中应用了线段包围盒等技术快速排除不需求交的情况，但是其求交时间仍占全部耗时的 80%以上。文献[3]提出了应用空间剖分技术以使得每条边不必与所有其它边求交的设想，但并未就该技术展开深入研究。姚辉学等[12]提出将两个多边形的公共包围盒范围划分为格网，然后将边归属于相应网格中，在边求交时只计算与所处理边位于同一网格内的边；但是该文献在处理边与网格关系时采用办法是判断边与所有网格的关系，同时该方法会导致一组边重复计算交点的问题，得出的结论是一个网格内边数在 80 ～100之间时效率最佳，这种程度的优化非常有限。

2 新算法的原理

以往算法一般将交点划分为进点和出点两类，对于交于顶点和边重合的情况，将其归类为进点或出点。与上述思路不同的是，本文将交点划分为普通交点与顶交点两类，普通交点和顶交点的定义如图1所示，多边形S和C相交，普通交点为I1、I2和I3，顶交点为C3、C4、S4；在进行跟踪获得输出多边形的时候，针对这两类交点的特点，构造了不同的跟踪策略，以此来确保输出结果的正确。跟踪策略及过程将在第5节讨论。

在效率优化上，边与边求交本身已经基本没有优化空间，更重要的是如何让边只与可能有交的边求交。本文的方法是：将顶点数目多的多边形的边划分到空间网格中，而在边划分到网格的过程中，采用了类似于直线段扫描转换Bresenham算法的技术，使得划分过程的效率达到最优；而求交点时则以另一个多边形的边来与网格中多边形的边求交，并通过简单的赋值和比较避免了重复求交问题。第4节将讨论边求交过程。

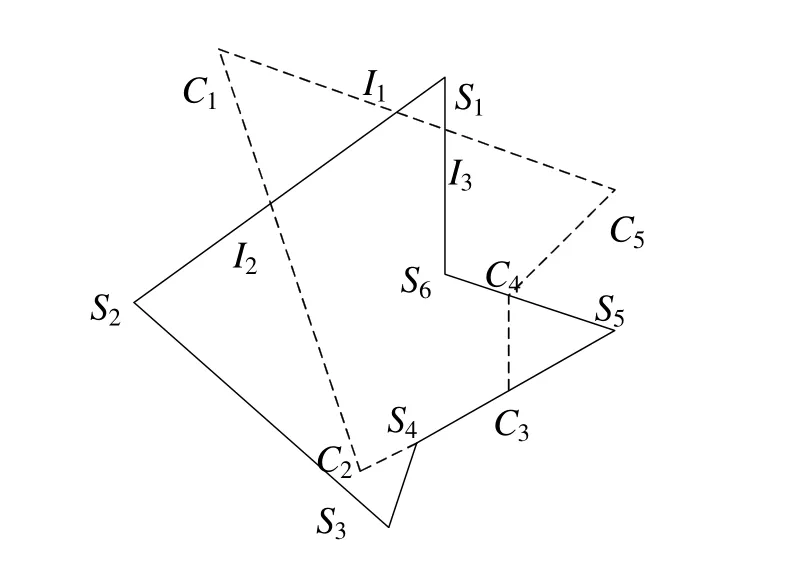
图1 普通交点和顶交点的定义

3 算法采用的数据结构

刘勇奎算法针对顶点和交点定义了不同的数据结构，虽然顶点的定义节省了1个指针，但是在遍历链表的时候将不得不额外区分顶点和交点；Greiner-Hormann算法中采用相同的数据结构表示顶点和交点，用1个boolean数据作为交点标志，在遍历节点时只需判断标志即可。本文以相同的数据结构表示顶点、普通交点和顶交点，链表结点定义为（其中 coordinates 表示坐标类型；vertexPtr表示指针）：

vertex={x,y: coordinates;

其中tag域表示节点的类型，值为0表示顶点，值1表示普通交点，值2表示顶交点；alpha域表示以参数形式表示的交点坐标，范围在0到1之间，当同一边上有多个交点时，利用该参数进行排序；cnt域用于避免重复求交；next域表示指向下一结点的指针；对于交点，other域指向另一链表对应交点。图2给出了对图1的两个多边形进行裁剪时形成的链表（结点内标出其 tag域的值）。

图2 对图1的多边形进行裁剪时算法产生的链表数据结构

4 交点判断与计算

网格划分的目的是减少参与求交的边数，如果网格划分的效率足够高且不同网格中的同一组边不发生重复求交，则划分越细则实际参与求交边数越少。统计表明，本文算法中每个网格平均边数在3 ～5个之间效率最优。根据多边形包围盒宽度、高度和多边形顶点数，划分为 Gx×Gy的网格，然后计算每个网格边长Δ及其倒数δ。

图3 边的网格划分算法

文献[12]采用对于每条边逐个判断网格是否与其相交，效率极低。构造了可以消除浮点除法运算的算法：边沿起点网格前进到终点网格，每次在主方向前进一个网格，而构造误差确定在另一个方向是否前进。定义误差ε为线段与副方向网格线的交点与网格线的差，如图3所示，对于垂直网格线1，其ε小于网格边长Δ，在副方向不前进，边经过网格(0,2)；对于垂直网格线 4，累计计算的ε大于Δ，副方向前进，边经过网格(3,2)和(3,3)。问题归结为如何计算ε初值以及递推公式，设起点所在网格为(i,j)，边起点到终点的差值为dx、dy，网格水平方向最小值为xmin，起点坐标为(x0,y0)，则初值和递推公式为

由于上式的作用是通过比较进行判断，因此将初值、步进值和比较参考值同时乘以dx，消除浮点除法运算。以x方向为主方向，向右上方前进时的网格化算法见算法1。

算法 1边v0v1的网格划分

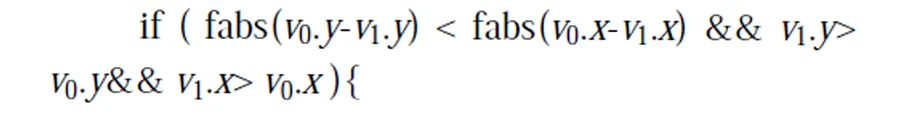
计算v0所在的网格并设置为当前网格;

算法1中，循环次数基本等于边所经过的网格数，最大不会超过max{Gx,Gy}，大部分情况仅需处理很少的网格，既不需判断多余网格，每个网格内运算量也非常小。

将边数较多的多边形进行网格划分后，以另一个多边形的边与该边所经过的每个网格内的边求交，采用与算法1基本一致的方法确定边经过的网格，然后求交，算法略。在数据结构中定义了cnt域，该值随着求交的边变化而增长，当网格内另一多边形边的cnt域值已经和求交边的值相同，则表示两者已经进行过求交，避免重复求交。

5 双策略跟踪得到输出多边形

针对交点和顶交点构造不同跟踪策略，交替使用2个跟踪策略，得到输出多边形。

遇到交点的跟踪策略是直接由一个链表切换到另一个链表，见算法2，其中PS和PE是参数，分别表示跟踪当前指针和跟踪起点指针。

顶交点的下一结点有3种可能：顶点、交点和顶交点。如下一结点为顶点和交点，通过判断该点与另一多边形位置关系来决定是否进行链表切换；如下一结点为顶交点，则当前结点与下一结点所形成线段可在另一多边形之内、边界上或之外。根据当前结点与下一结点中点与另一多边形位置关系来决定是否进行链表切换：如果中点在另一多边形之内或边界上，不切换链表，否则切换链表；根据下一结点类型选择继续采用哪个跟踪策略。

以上算法根据交点类型交替、递归地调用2种跟踪策略函数，跟踪过程非常简洁、直接，算法易于实现，但会带来一定函数调用开销。

6 算法效率分析与比较

算法包括3个主要部分：多边形网格划分、边求交、跟踪，设多边形边数分别为 m、n，下面分析平均情况下的时间复杂度。

多边形网格划分，每个多边形边所经过网格数不确定，与多边形边数、形态等都有关，测试中平均经过 2 ～5个网格，时间复杂度为O(max(m,n))；边求交，由于网格划分很细，边只与其所经过网格的边求交，平均情况下时间复杂度为O(min(m,n))；跟踪，遍历链表的时间复杂度为O(m+n+k×2)，其中k为交点个数。

选取了一些不同顶点数（N为2多边形顶点数之和）的多边形，测试了算法各个步骤的执行时间。新算法与参照算法都在VC6.0实现，时间测试使用高精度时间函数QueryPerformanceFrequency()，运行在主频 3.0G的普通微机，测试结果如表1所示。

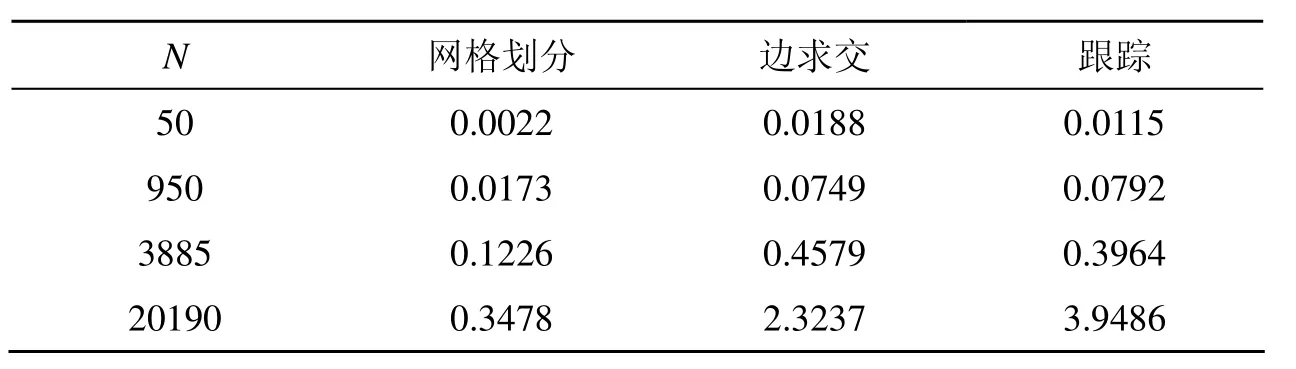
表1 算法3个主要步骤所需时间的比较(ms)

从表1中可以看出：① 网格划分的效率非常高，在整个算法中所占的时间比例很小；② 求交所用时间与跟踪所用时间在一个量级，这较之于一些传统算法有了较大的改进。

将本文算法与 Vatti算法、Leonov算法和Schutte算法进行对比，比较结果如表2所示。新算法比Vatti算法、Leonov算法的效率高出1 ～2个数量级，Schutte算法效率很低，不具可比性。文献[9]对刘勇奎算法、Vatti算法和Greiner-Hormann算法进行了比较，其中Greiner-Hormann算法耗时约为 Vatti算法的一半，刘勇奎算法耗时约为Vatti算法的三分之一。结合该比较结论可以看出，本文算法的效率也远优于Greiner-Hormann算法和刘勇奎算法。在表2中，当多边形点数较多时，Schutte算法无法正确执行，用“*”表示。

表2 新算法与Vatti算法、Schutte算法和Leonov算法运行时间的比较(ms)

7 结 束 语

网格划分是计算机图形学中的一项常用技术，文献[12]实际也采用了类似技术，本文创新在于划分过程中边的处理方法以及避免重复求交的方法，显著提升求交效率；同时本文提出了双策略跟踪的方法，在跟踪环节解决算法的鲁棒性，对于交点落在边上、边重合等各种情况都确保结果正确，这也有别于传统算法。

在适用性方面，本文算法存在如下局限：算法主要适用于多边形边数较多的场合，当边数少于 15条时，可以不进行网格划分；对于多边形的边分布比较极端的情况，如过多的边集中在一个网格内，算法的效率优势并不明显。

[1] Rivero M L ,Feito F R. Boolean operations on general planar polygons [J]. Computers and Graphics,2000,24(6): 881-898.

[2] Peng Y,Yong J H,Dong W M,et al. A new algorithm for boolean operations on general polygons [J].Computers and Graphics,2005,29(1): 57-70.

[3] Schutte K. An edge labeling approach to concave polygon clipping [EB/OL]. (2007-11-7) [2010-7-12]http://citeseerx.ist.psu.edu/viewdoc/summary? doi=10.1.1.23.6997

[4] Leonov M V,Nikitin A G. A closed set of algorithms for performing set operations on polygonal regions in the plane [EB/OL]. (2002-11-24)[2010-7-12] http://www.complex-a5.ru/polyboolean/downloads/polybool_eng.pdf

[5] 朱雅音,王化文,万 丰,等. 确定两个任意简单多边形交、并、差的算法[J]. 计算机研究与发展,2003,40(4): 576-583.

[6] Weiler K,Atherton P. Hidden surface removal using polygon area sorting [C]//Proceedings of the SIGGRAPH’77. New York: ACM Press,1977:214-222.

[7] Vatti B R. A generic solution to polygon clipping [J].Communications of the ACM,1992,35(1): 56-63.

[8] Greiner G,Hormann K. Efficient clipping of arbitrary polygons [J]. ACM Transactions on Graphics,1998,17(2): 71-83.

[9] 刘勇奎,高 云,黄有群. 一个有效的多边形裁剪算法[J]. 软件学报,2003,14(4): 845-856.

[10] 鲍虎军,彭群生. 一个有效的多边形裁剪算法[J].自动化学报,1995,22(6): 741-744.

[11] 刘勇奎,颜 叶,石教英. 一个有效的多边形窗口的线裁剪算法[J]. 计算机学报,1999,22(11):1209-1214.

[12] 姚辉学,卢章平. 一种任意复杂程度二维多边形的求交算法[J]. 工程图学学报,2006,27(2): 127-131.