基于鲁棒滑模观测器的高超声速飞行器双环滑模控制①

宋 超，赵国荣，陈 洁

(海军航空工程学院控制工程系，烟台 264001)

基于鲁棒滑模观测器的高超声速飞行器双环滑模控制①

宋 超，赵国荣，陈 洁

(海军航空工程学院控制工程系，烟台 264001)

针对高超声速飞行器非线性动力学系统中存在的高度非线性、多变量耦合及参数不确定等问题，设计了一种基于鲁棒滑模观测器的双环滑模控制方法。该方法首先利用设计的鲁棒滑模观测器在线估计系统的不确定性及未知干扰，在此基础上，通过设计滑模变结构控制器来实现对不确定性的抑制控制，从而实现对制导指令的鲁棒输出跟踪。仿真结果验证了该方法能较理想地估计干扰，保证系统良好的鲁棒性。

高超声速飞行器;不确定性;滑模观测器;滑模控制

0 引言

近年来，高超声速飞行器作为导弹突防及实现远程精确打击的新途径成为研究热点［1］。高超声速飞行器由于飞行环境大范围变化，机身的弹性变形、气动参数变化和外界干扰都不可避免，致使所建立的飞行器动力学模型存在高度非线性、强耦合及不确定性，且表现为非匹配的不确定性［2］。而且机体/发动机一体化技术使得高超声速飞行器弹性机体、推进系统以及结构动态之间的耦合更强，模型的非线性度也更高，而飞行器飞行过程中各种复杂的力学过程不可能完全精确考虑在用于控制设计的飞行器控制模型中，且飞行过程往往又会受到各种事先无法完全预知的扰动［3-4］。因此，如何在系统存在不确定性及未知干扰条件下，保证系统实现稳定跟踪控制尤为重要。

鲁棒滑模观测器通过滑模和相应的控制策略实现对系统状态及不确定项的估计，在很多领域得到应用［5-6］。文献［7］设计的滑模观测器对外部的干扰在线估计，进行前馈控制，提高了控制系统的鲁棒性。文献［8-9］研究了利用非线性干扰观测器消除系统不确定性和外界未知干扰，增强了系统的鲁棒性，并成功地用于机器人、导弹的控制中。文献［10］由滑模观测器产生控制力矩，用来稳定和削弱再入过程干扰项，增加了系统鲁棒性。滑模变结构控制本质是一类非线性鲁棒控制，只要系统状态达到滑动模态区，匹配的不确定性就对系统完全无影响，非常适于解决不确定系统的跟踪问题［11-12］。

本文针对飞行器飞行过程中存在的系统不确定性及各种未知干扰情况，利用鲁棒滑模观测器观测系统状态及不确定性。对引入观测器的系统采用滑模变结构控制方法，实现高超声速飞行器的跟踪控制。

1 模型描述

假设1:不考虑飞行器的挠性，即视为刚体。

选取状态变量x1=［αβγV］T，x2=［ωxωyωz］T，控制输入u=［δxδyδz］T，系统输出y=x1=［αβγV］T。其中，α、β、γV为飞行器的攻角、侧滑角和速度滚转角;ωx、ωy、ωz为飞行器绕弹体坐标系转动角速度。建立飞行器运动学和动力学方程如下:·

简化式(1)和式(2)，则系统模型可写成:

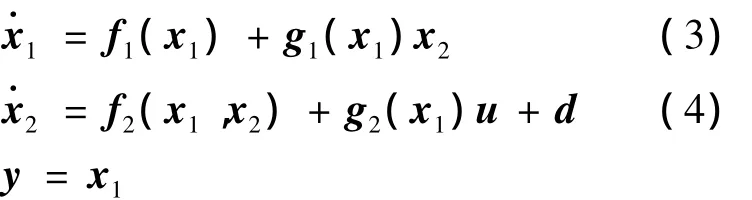
式中f1(x1)、f2(x1，x2)、g1(x1)、g2(x1)为对应的矩阵;d为模型耦合项、组合干扰等不确定项。

令x=［x1x2］T，则上述模型可写成:

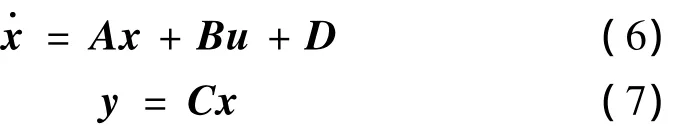
式中A、B、C定义为系统的状态矩阵、输入矩阵和输出矩阵;D为非线性不确定项。

飞行器控制系统的任务是在不超过控制执行机构所能提供的控制量限制的前提下，实现对制导系统给出的气流角指令yd的跟踪［15］。

2 鲁棒滑模观测器设计

假设2:跟踪指令yd及其一阶导数存在且有界。

假设3:不确定项d是有界的，即满足‖d‖≤δ，其中δ为未知上界正常数。

针对非线性系统(6)，鲁棒滑模观测器［16］设计为

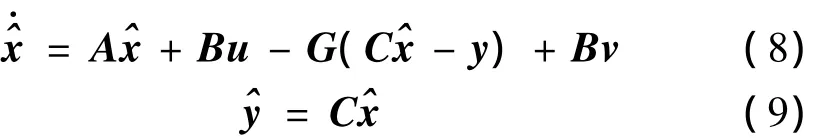
定义非线性不确定系统的状态与观测器状态偏差为e=。

假设4:状态偏差始终有界的，即满足‖e‖≤ε，其中ε为未知上界正常数。实际情况中，该条件通常是满足的。

由式(6)和式(8)得出偏差系统方程为

定义A0=A-GC，则式(10)写成:

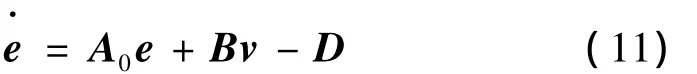
若偏差系统的状态变量渐进或有限时间收敛到原点，则实现了系统的状态估计。

为设计鲁棒滑模观测器，先将滑模面设计为线性滑模形式:

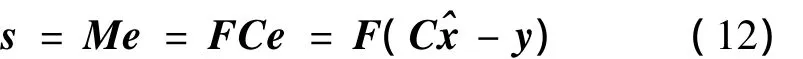
式中F为待设计矩阵，M=FC。

因此，滑模设计问题归结为参数矩阵F的设计问题。考虑到由观测器输入不连续可导致的系统抖振，设计如下滑模策略用于消除抖振［17］:

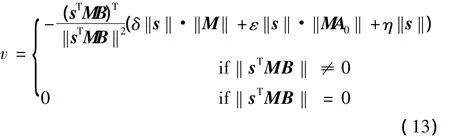
式中 0＜η＜1为待设计参数。

令e=［e1e2］，将偏差系统(11)写成分块形式:

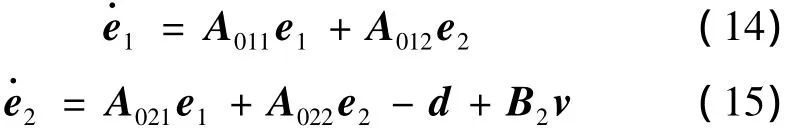
式中 ［A011，A012，A021，A022］=A;［0，B2］=B。

将滑模(12)写成分块的形式:

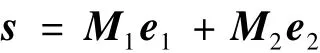
式中 ［M1，M2］=M。

定义如下矩阵:

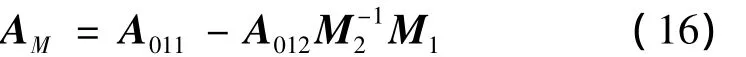
定理:对不确定系统(6)的鲁棒滑模观测器(8)，采用滑模(12)和策略(13)，设计参数矩阵F，使得式(16)中的AM为Hurwitz矩阵，则鲁棒滑模观测器(8)对系统(6)的不确定部分具有鲁棒性，可渐进估计出系统状态。

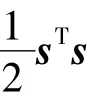
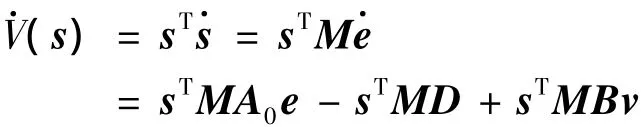
将滑模策略式(13)代入上式，有

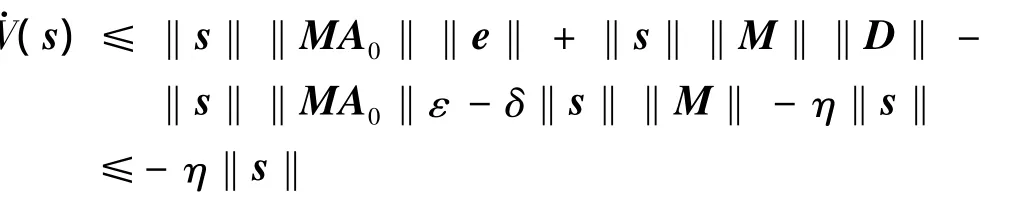
由Lyapunov全局稳定定理，偏差系统(10)在有限时间内到达滑模面。此时有s=0，即

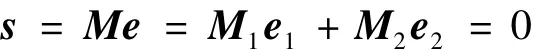
由上式可得e2=-1e1，代入式(15)有

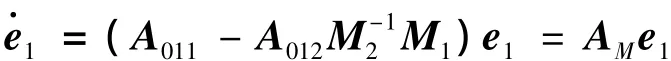
设计参数矩阵F，使AM为Hurwitz矩阵，则上述系统渐进稳定，即偏差系统(10)到达滑模态后，将渐进收敛到平衡点e=0，其收敛速度由AM的特征值确定。

3 滑模控制器设计

根据时间尺度分离假设，设计双环飞行控制系统，内外环均采用滑模控制。控制结构如图1所示。

3.1 未知干扰的估计

由图1可知，为消除不确定性和未知干扰对系统性能的影响，采用鲁棒滑模观测器对系统的干扰进行估计。利用系统估计信息和输出信息，可实现未知干扰的在线估计。

由式(6)定义未知干扰的估计为

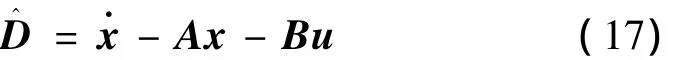
因系统的状态不完全可测，故用滑模观测器估计出的系统状态替换式(17)中的系统状态信息:

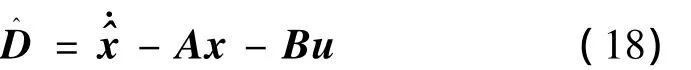
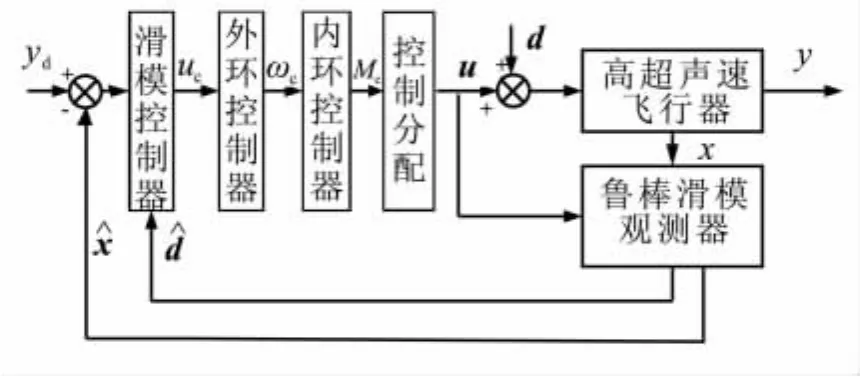
图1 基于滑模观测器的控制结构图Fig.1 Control structure figure based on SMO

3.2 滑模控制

外环滑模控制器将飞行器角速度向量ω当成虚拟的命令ωc(即认为内环的控制效率为1)。内环滑模控制器产生必需的向量力矩Mc来跟踪给定的角速度命令ωc。

令uc为需设计的外环滑模控制器的输入，使跟踪误差沿滑模面趋近原点。

选择积分型切换函数，滑模面上的气流角跟踪误差ec=yd-=xd-的各分量渐进收敛于0。

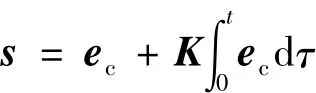
式中K=diag［k1k2k3］＞0。

滑模变结构控制律为

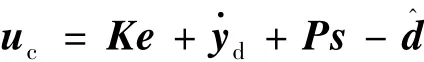
式中为由式(11)得出的不确定项的估计值;P=diag［p1p2p3］＞0。

4 仿真验证

为简化控制器设计，忽略惯性积项。飞行器主惯量Jx、Jy、Jz分别取 1000、7600、7700 kg·m2。取K=diag［0.2 0.1 0.1］;p1=p2=p3=5;γd=10;初始条件x1(0)=［0.2° 0.3° 0.1°］T，x2(0)=［0 0 0］T;=［0.3 0.1 0.2］T;期望跟踪信号yd=［0°0° 0°］。

为验证非线性观测器的性能，系统干扰分别取为正弦时变干扰、余弦时变干扰和正态分布随机干扰。即d=［d1d2d3］T，其中d1=0.25sin(4πt);d2=0.05cos(4πt);d3=0.06 ×rand，单位为(°)/s2。仿真结果如图2～图5所示。图中，下标“r”表示真实值;下标“e”表示估计值。

由仿真图2可看出，本文设计的滑模观测器能很好地对系统的状态量进行观测，且跟踪指令上升时间较短。图3表明，姿态角跟踪误差渐进收敛于零，整个系统具有良好的跟踪性能。图5给出设计的观测器观测干扰的情况。可看出，设计的滑模观测器能很快观测出外加干扰。整个仿真表明，本文设计的控制器具有更好的鲁棒性，能够更好地克服系统中参数不确定性和外来干扰。

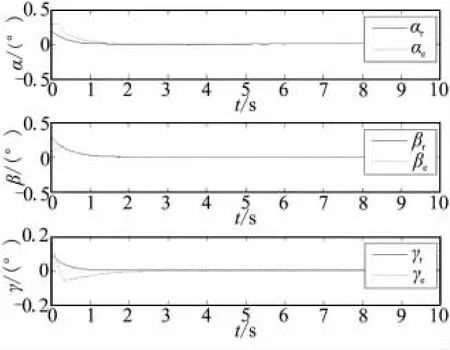
图2 观测器对姿态角的观测曲线Fig.2 Attitude angle observe curves

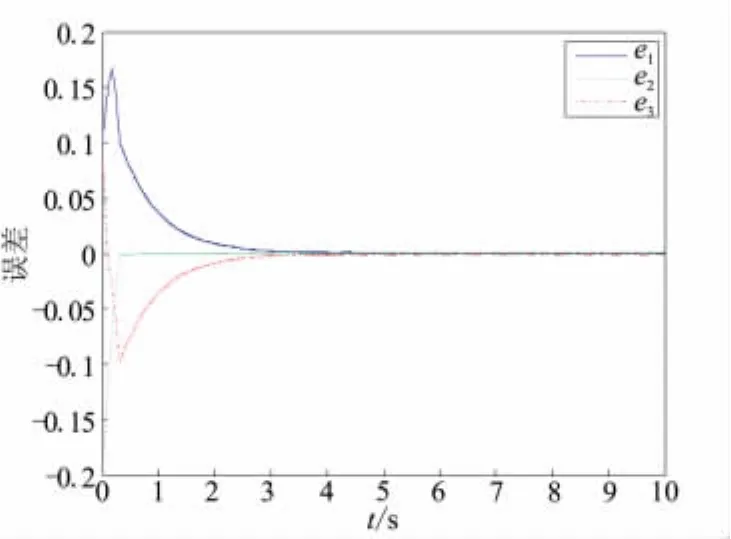
图3 观测器姿态角跟踪误差曲线Fig.3 Attitude angle tracking error curves

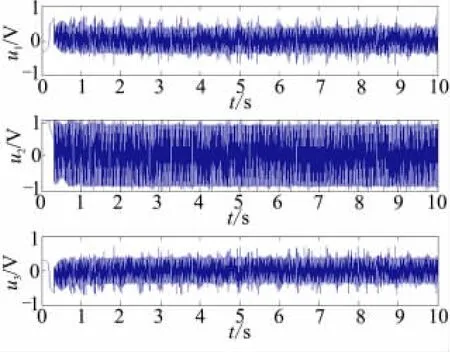
图4 滑模控制器的输出曲线Fig.4 Controller output curves

图5 实际干扰及观测值Fig.5 Real disturbance and estimate value

5 结论

在对高超声速飞行器数学模型充分分析的基础上，设计了鲁棒滑模观测器对系统不确定性及各种干扰进行观测，然后采用滑模变结构控制策略，实现对制导指令的跟踪控制。研究表明，采用滑模观测器后，能对系统各种未知干扰和气动参数的不确定性进行观测，系统性能得到明显改善。由仿真结果可看出，该控制器具有良好的跟踪性能，对不确定性及外界干扰具有鲁棒性。

［1］Jorris T R.Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no-fly zone constraints［D］.Alabama:Air University，2007.

［2］Maj Mirmirani，Chivey Wu，et al.Modeling for control of a generic airbreathing hypersonic vehicle［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.San Francisco，California:AIAA ，2005:1-19.

［3］Shahriar keshmiri，Richard Colgren，Maj Mirmirani.Six-DOF modeling and simulation of a generic hypersonic vehicle for control and navigation purposes［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Keystone，Colorado:AIAA，2006:1-10.

［4］尉建利，于云峰，闫杰.高超声速飞行器鲁棒控制方法研究［J］.宇航学报，2008，29(5):1526-1530.

［5］张袅娜，冯勇，邱东.非线性不确定系统的鲁棒滑模观测器设计［J］.控制理论与应用，2007，24(5):715-718.

［6］鲍晟，冯勇，孙黎霞.非线性不确定系统的鲁棒滑模观测器设计［J］.哈尔滨工业大学学报，2004，36(5):613-616.

［7］Charles E H，Yuri B S.Sliding mode disturbance observer based control for a reusable launch vehicle［J］.Journal of Guidance，Control，and Dynamics，2006，29(6):1315-1328.

［8］Chen Wen-hua，Ballance D J，Gawthrop P J.A nonlinear disturbance observer for robotic manipulators［J］.IEEE Transactions on Industrial Electronics，2000，47(4):932-938.

［9］Chen Wen-hua.Nonlinear disturbance observer-enhanced dynamic inversion control of missiles［J］.Journal of Guidance，Control and Dynamics，2003，26(1):161-166.

［10］张阳.滑模观测器在临近空间高动态UAV中的应用［J］.航空学报，2008，29(增刊):123-126.

［11］Capisani L M，Ferrara A，Maqnani L.Design and experimental validation of a second-order sliding-mode motion controller for robot manipulators［J］.International Journal of Control，2009，82(2):365-377.

［12］方勇纯，卢桂章.非线性系统理论［M］.北京:清华大学出版社，2009:21-81.

［13］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2008:28-48.

［14］赵汉元.飞行器再入动力学和制导［M］.长沙:国防科技大学出版社，1997:23-86.

［15］陈洁，周绍磊，宋召青.基于不确定性的高超声速飞行器动态面自适应反演控制系统设计［J］.宇航学报，2010，31(11):2550-2556.

［16］程月华，姜斌，孙俊，等.基于滑模观测器的卫星姿态控制系统滑模容错控制［J］.上海交通大学学报，2011，45(2):190-194.

［17］李炜，程应峰，许德智.多变量未知非线性系统容错逆控制方法［J］.华中科技大学学报(自然科学版)，2011，39(8):114-118.

Dual-loop sliding mode control for hypersonic aircraft with robust sliding mode observer

SONG Chao ，ZHAO Guo-rong ，CHEN Jie
(Department of Control Engineering，Naval Aeronautical and Astronautical University，Yantai264001，China)

To solve the problem that hypersonic aircraft＇s nonlinear dynamics system is highly nonlinear，multivariable coupling and includes uncertain parameters，a sliding mode control method based on robust sliding mode observer(SMO)was designed.At first，robust sliding mode observer was used to estimate the uncertainty and disturbance of the system on line.Then，sliding mode controller was adopted to achieve unknown disturbance rejection.The approach can realize robust output tracking to guidance order.Simulation results show this method can estimate the disturbance well and enhance the robust performance of the system.

hypersonic aircraft;uncertainty;sliding mode observer;sliding mode control

V448

A

1006-2793(2012)04-0438-04

2011-12-16;

2012-01-13。

国家自然科学基金项目(61004002);航空科学基金项目(20110184001)。

宋超(1983—)，男，博士生，主要研究方向为飞行器制导与控制。E-mail:schhh_1983@126.com

(编辑:吕耀辉)