基于面元法的栅格翼翼身组合体高超声速气动特性研究①

周 张，胡 凡，于 勇

(1.北京理工大学 宇航学院，北京 100081;2.国防科技大学航天与材料工程学院，长沙 410073)

基于面元法的栅格翼翼身组合体高超声速气动特性研究①

周 张1，胡 凡2，于 勇1

(1.北京理工大学 宇航学院，北京 100081;2.国防科技大学航天与材料工程学院，长沙 410073)

栅格翼是由外部框架和内部栅格布置形成的空间多升力面系统，其在高超声速状态具有突出优点。文中结合高超声速流动特点，考虑头部激波及弹身上洗干扰，基于面元法建立栅格翼翼身组合体高超声速气动特性计算模型，根据研究对象特点自动划分面元，进而完成典型栅格翼翼身组合体高超声速气动特性计算，并与数值计算结果进行对比分析。结果表明，在研究范围内，栅格翼翼身组合体高超声速气动特性面元法计算结果与数值计算结果吻合较好，前者较后者相对误差绝对值随攻角增加而增大。

栅格翼;高超声速;气动特性;面元法

0 引言

栅格翼是由外部框架和内部栅格布置形成的空间多升力面系统，其主要优点有［1］:(1)升力特性好;(2)压心漂移小，用作气动控制铰链力矩小，降低了对舵机的要求;(3)强度质量比大;(4)栅格翼展向尺寸小，可以紧贴弹体折叠安装，减小尺寸。栅格翼气动特性主要受其内部流态影响。其中，亚声速状态栅格翼阻力特性和控制效率与平板翼类似;跨声速状态流动阻塞，阻力显著升高;低超声速状态激波角较大，激波与格壁相交并经格壁反射后离开栅格面，反射激波带来较大阻力;随着马赫数增加，高超声速状态激波角减小，激波不再与栅格面相交，其阻力特性、升力特性明显提高，具有良好应用品质。

国内外栅格翼工程应用主要集中于亚、跨、超声速(如俄罗斯R-77空-空导弹、Club潜射巡航导弹、OTR-21短程弹道导弹，美国MOAB炸弹、MALD干扰弹、SPAD空基反潜武器，印度SLCM潜射巡航导弹，中国CZ-2F飞船逃逸救生系统)，从公开发表的文献分析，其高超声速领域应用较少，相关研究以计算为主，实验研究较少。随着航空航天技术的不断发展，人们对飞行器飞行速度、控制精度的需求不断提高，在加工工艺、防热材料技术不断进步的基础上，栅格翼较平板翼的显著优势及其优良高超声速性能必将带来其高超声速领域应用的不断拓展，研究栅格翼高超声速气动特性具有重要理论与实践意义。

国内外关于栅格翼高超声速气动性能研究主要有数值计算与工程计算，前者计算稳定性与精度较高，但计算效率较低，后者反之。本文致力于研究栅格翼翼身组合体高超声速气动特性工程计算问题。目前，国内外该领域研究多沿用超声速状态所取方法，即基于激波-膨胀波理论建立模型进行计算［2］，较为复杂，且对头部激波影响未加以修正。为简化计算，提高精度，本文充分结合高超声速流动特点，考虑头部激波及弹身上洗干扰，基于面元法建立栅格翼翼身组合体高超声速气动特性计算模型，完成其高超声速气动特性计算，并与数值计算结果进行对比分析。

1 数学模型

面元法利用平面四边形或三角形面元来代替实际飞行器表面微元，通过计算各平面面元压强，考虑摩阻与底阻，叠加即可得到飞行器整体气动特性。本文根据栅格翼翼身组合体不同部件特点选取其表面面元压强系数计算方法，修正头部激波及弹身上洗干扰，并考虑摩阻与底阻对整体气动力贡献。

1.1 压强系数计算方法

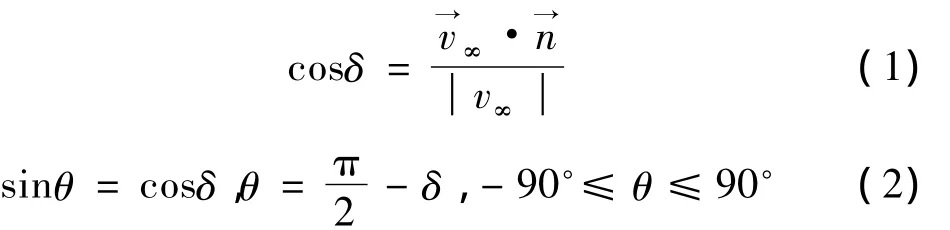
当0°≤θ≤90°时，气流作用的物面处于迎风区;当-90°≤θ≤90°时，气流作用的物面处于背风区。

高超声速条件下，迎风区压强系数计算方法主要有修正牛顿方法、Dahlem-Buck方法、切楔法、切锥法。背风区压强系数计算方法主要有牛顿方法、Acm经验方法、Prandtl-Meyer方法。本文针对栅格翼翼身组合体特点，弹体与栅格翼压强系数采用不同方法计算。弹体迎风区采用 Dahlem-Buck方法，背风区采用Prandtl-Meyer方法;栅格翼格间流动呈二维特征［3］，其迎风区采用切楔法计算，背风区仍采用Prandtl-Meyer方法。

1.2 干扰修正

(1)头部激波干扰修正

高超声速条件下，受头部激波影响，激波后面元当地气流参数不同于来流参数，本文采用爆炸波理论求解零攻角状态头部激波后气流参数。非零攻角情况采用等效体理论转换为零攻角问题计算，提高精度。

(2)弹身上洗修正

当攻角α≠0°时，栅格翼处于弹身上洗流场中，栅格翼面元当地气流参数由修正后来流参数与弹身上洗参数共同决定，栅格翼面元气流参数:

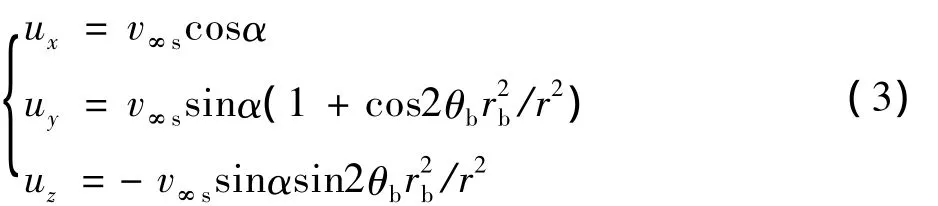
式中v∞s为干扰修正来流参数;rb为弹身半径;r为面元中心距弹轴距离;θb为面元中心周向角。

1.3 摩擦阻力计算

本文研究范围内，平板摩擦阻力系数:

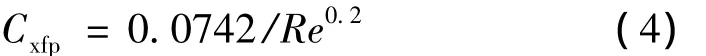
分别计算弹身与栅格翼各格片摩擦阻力系数，考虑形状影响后的摩擦阻力系数:

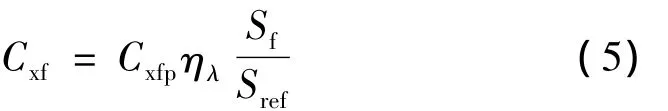
式中Cxfp为平板摩擦阻力系数;ηλ为形状修正系数，弹身取值由其长细比确定，栅格翼格片取值为1;Sf为沾湿面积，对于弹体部分取弹体侧表面积，栅格翼格片取2倍格片平面面积;Sref为参考面积。

1.4 底部阻力计算

底部阻力系数采用经验公式计算:

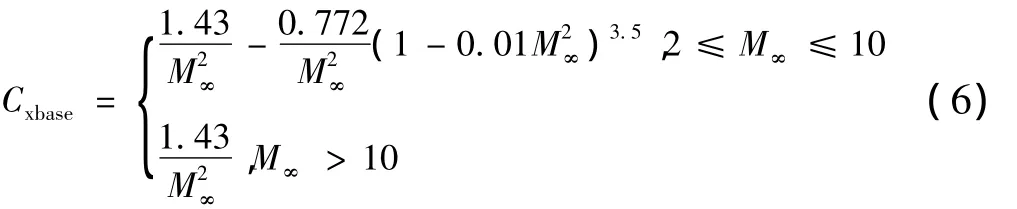
2 算例分析

栅格翼高超声速领域应用与实验研究较少，本文取图1所示为典型栅格翼翼身组合体外形为研究对象，用本文方法计算其气动特性，计算马赫数范围为8～12，攻角范围为0°～10°，并将计算结果与数值计算结果进行比较分析。图1中，尺寸单位mm。

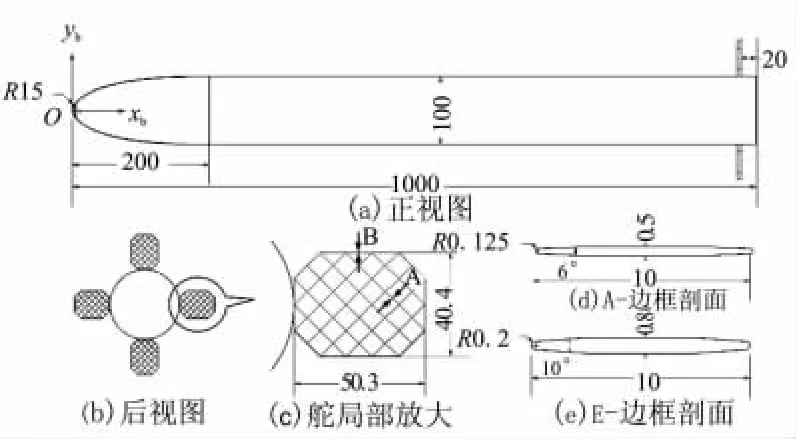
图1 栅格翼翼身组合体气动外形Fig.1 Grid fin-body configurations

2.1 面元法计算

面元离散采用参数化方法自动完成。弹身网格划分沿轴向与周向同时进行，划分结果如图2所示。弹体系中弹身各面元法向矢量、中心坐标、面积可解析得到。栅格翼面元离散以各格片为单位进行，划分结果如图3所示。建立格片直角坐标系，该坐标系中各面元法向矢量、中心坐标、面积可直接得到，经坐标转换后，即可得到弹体坐标系中相应栅格翼面元相应数值。

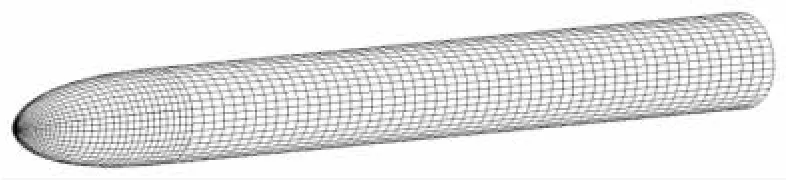
图2 弹体面元离散Fig.2 Surface element modeling of body

图3 栅格翼格片面元离散Fig.3 Surface element modeling of grid fin panel

根据面元划分结果，采用面元法即可得到栅格翼翼身组合体表面压强分布，叠加后即可得到其整体气动特性。

2.2 数值计算

采用数值方法计算图所示外形气动特性，计算马赫数为 8、10、12;计算攻角为 0°、2°、4°、6°、8°、10°。网格划分［4］如图4所示，对称面马赫数分布如图5所示。可见，栅格翼当地气流参数与自由来流差异较大，其气动特性计算必须考虑头部激波影响;该状态栅格翼前缘所致激波与格片不相交。

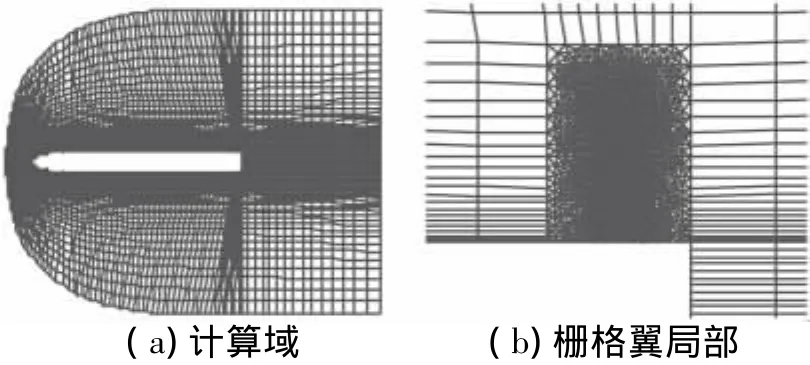
图4 对称面网格Fig.4 Mesh of symmetry plane

图5 对称面马赫数分布Fig.5 Mach number distribution of symmetry plane

2.3 计算结果与对比分析

本文所用面元法与数值方法气动特性计算结果如图6所示，前者较后者相对误差如图7所示。分析可得，研究范围内，面元法与数值方法所得结果趋势一致;轴向力系数计算结果前者小于后者，误差绝对值约保持在12%以内;法向力、俯仰力矩系数误差特性基本一致，面元法计算结果大于数值计算结果，误差绝对值保持在约15%以内;面元法气动特性计算结果相对误差绝对值随攻角增加而增大。

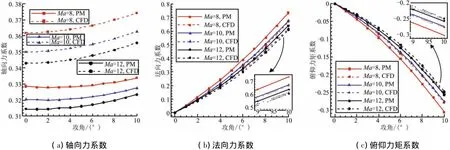
图6 栅格翼翼身组合体高超声速气动力特性Fig.6 Hypersonic aerodynamic characteristics of grid fin-body configuration

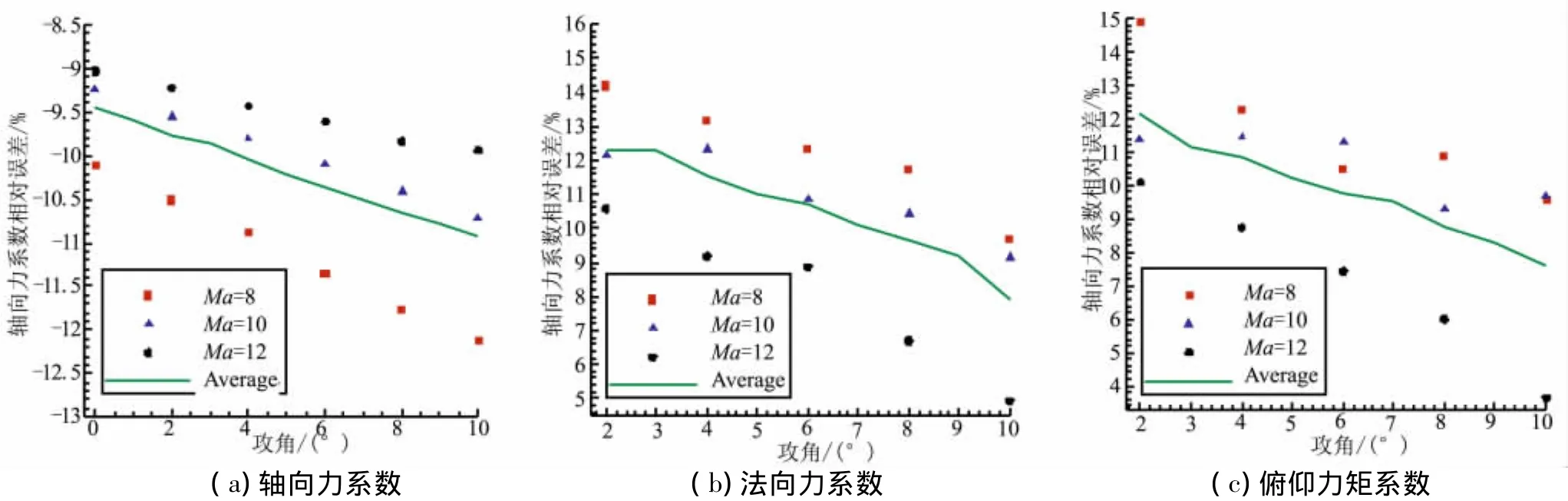
图7 面元法计算结果误差分布Fig.7 Deviation results obtained by surface element method

3 结论

(1)在研究范围内，栅格翼翼身组合体高超声速气动特性面元法计算结果与数值计算结果趋势一致，吻合较好。

(2)轴向力系数计算结果前者小于后者，法向力、俯仰力矩系数反之。

(3)面元法气动特性计算结果相对误差绝对值随攻角增加而增大。

［1］Simpson G M，Sadler A J.Controls:a comparison with conventional，planar fins［C］.Sorrento，Italy:RTO AVT Symposium.1998.

［2］Theerthamalai P，Nagarathinam M.Aerodynamic analysis of grid-fin configurations at supersonic speeds［J］.Journal of Spacecraft and Rockets，2006，43(4):750-756.

［3］Lu Zhong-rong，Su Wen-han.Hairpin vortices in the wake of grid fin［J］.Chinese Journal of Aeronautics，2001，14(4):200-204.

［4］Deng You-qi，Ma Ming-sheng，Zheng Ming.Navier-Stokes computation of grid fin missile using hybrid structured-unstructured grids［J］.Chinese Journal of Aeronautics，2006，19(4):304-308.

Hypersonic aerodynamics research of grid fin-body configurations base on surface element modeling

ZHOU Zhang1，HU Fan2，YU Yong1
(1.School of Aerospace，Beijing Institute of Technology，Beijing 100081，China;2.College of Aerospace and Material Engineering，National University of Defense Technology，Changsha 410073，China)

Grid fin is a space lifting surface formed by the external frame and internal web，which is of outstanding advantages in hypersonic state.Hypersonic aerodynamic characteristics analysis model of grid fin-body configuration is established based on surface element method considering the characteristics of hypersonic flow，the head shock wave and body upwash interference were taken into account as well.Surface element was built automatically according to grid fin-body configuration geometry feature.Grid fin-body configuration hypersonic aerodynamic characteristics were obtained and agreed well with numerical results.The deviation increases with angle of attack.

grid fin;hypersonic;aerodynamics character;surface element modeling

V411

A

1006-2793(2012)04-0442-04

2012-02-16;

2012-04-04。

周张(1986—)，男，博士生，研究方向为飞行器气动外形设计优化。E-mail:zhouzhang_bit@gmail.com

(编辑:吕耀辉)