火箭入轨的大偏航非线性鲁棒自适应控制方法①
刘新建,叶成敏,张立佳,卢亮亮,张利宾
(1.国防科技大学 航天与材料工程学院,长沙 410073;2.北京宇航系统与工程研究所,北京 100076)
火箭入轨的大偏航非线性鲁棒自适应控制方法①
刘新建1,叶成敏2,张立佳2,卢亮亮2,张利宾2
(1.国防科技大学 航天与材料工程学院,长沙 410073;2.北京宇航系统与工程研究所,北京 100076)
火箭入轨通常是沿标准轨道面的飞行控制,常规发射任务只需侧向小偏航角校正,但当今一些特殊的入轨任务要求火箭制导控制能侧向大偏航角飞行,以克服较大初始侧向偏差对末级火箭入轨的影响。文中提出了一种末级火箭的侧向大偏航非线性自适应组合制导控制方法,结合土星-5火箭IMG方法和航天飞机LTG方法各自的优点,进行了大偏航角的非线性耦合补偿修正,并对动力飞行过程的迭代算法进行了鲁棒稳定性改造。基于姿态喷嘴开关控制的六自由度数值仿真表明,提出的控制策略和算法简单可靠、稳定性好、精度高,在火箭入轨控制和空间飞行器变轨控制中具有参考和应用价值。
火箭入轨;制导与控制;自适应控制;大偏航非线性控制;空间快速响应
0 引言
未来空间运输和空间应急救援等快速响应任务,对火箭大偏航控制方法提出了特殊需求,如空间飞行器末级火箭如果具有一次性直接入轨控制能力,可大大缩短入轨时间,几小时内可实现从200 km低轨到上万公里高轨的直接快轨运输,但200 km基础级火箭分离的初始偏差,经过几个小时的滑行,速度误差对位置具有累计放大效应,尤其是侧向偏差需大偏航角的控制才能校正轨道平面。某些特殊飞行任务希望一次性实现异面机动变轨,比多次轨道面旋转调整,再进行其他轨道根数控制的方法要快得多,同样离不开大偏航角的变轨控制。经典火箭入轨控制方法通常有:(1)火箭基于标准轨道的摄动制导,利用小偏差理论对轨道进行误差校正,显然不能适应大偏差干扰的控制;(2)不依赖标准轨道,只与边界条件相关的显式迭代制导或自适应制导方法,在适应纵向初始大偏差的控制精度方面较摄动制导方法有了较大改进,这其中的典型代表是美国土星-5号运载火箭IMG显式迭代制导方法[1-3]和航天飞机 LTG线性正切制导律方法[4-5],这些方法应用时,通常约束侧向通道的偏航角小于10°,近似实现纵向和侧向通道的解耦控制,因为IMG给出的控制律是按小偏航角进行了线性化假设推导的。
国外 Lu Ping[6]、Calise A J[7]、Gath[8]对大气层内的显式迭代控制进行了研究,但其也利用了线性化假设如小侧滑角。Muratore J F[3]指出空间应急救援在控制方法上需解决火箭一次性直接入轨的大偏航非线性控制与定点入轨控制2个关键问题。Strandmoe S[9]在关于低轨ATV的变轨控制中也没涉及大偏航非线性控制。国内最近关于火箭自适应控制的研究(茹家欣、陈新民、吴楠等[10-13])均未涉及大偏航角非线性飞行控制的情况。可见,国内外对一次性直接入轨可能存在的大偏航非线性控制问题研究较少。
本文根据火箭飞行动力学耦合特点,吸收IMG和LTG方法的各自的优点,经过改造提出了一种火箭大偏航非线性鲁棒自适应控制方法。
1 大偏航非线性鲁棒自适应控制策略和方法
火箭在发惯系真空段的运动微分方程如下:

式中φ、ψ是箭体在发射惯性系中的俯仰、偏航姿态角;P是发动机的轴向推力;gx、gy、gz是地球引力加速度;m0、˙m是火箭的初始指令和燃料秒流量。
从方程(1)可看出,纵向运动的俯仰角φ不影响侧向Z分量的运动,即侧向运动只受偏航角的控制;但侧向运动影响纵平面内的运动控制,偏航角越大,耦合影响越强烈。
如果利用变分与最优控制原理,不作小偏航角简化假设,重新进行理论推导,那么这种方法得到关于俯仰角和偏航角的非线性最优控制将是隐式的包含边界条件的多变量耦合非线性方程组,而不是显式的解耦方程,计算量大不适合闭路控制。
观察方程(1),动力学耦合是一种单向耦合,只有侧向偏航角影响纵平面的运动。为此,分别利用IMG的侧向控制律和LTG的纵向控制律,构造一种大偏航非线性鲁棒自适应组合迭代制导方法和算法,可简化大偏航非线性控制问题,步骤如下:
(1)利用IMG侧向通道的显式公式,根据初始偏差和侧向终端边界条件计算偏航角指令,并对偏航角限幅(根据侧向偏差事先优化计算偏航角幅值如最大40°,幅值与初始偏差有关,因为过大浪费燃料,过小不能有效校正轨道平面);
(2)利用动力学单向耦合的特点,根据大偏航角对俯仰通道的耦合,补偿修正其耦合影响;
(3)在LTG预测公式的基础上,根据改造的纵向迭代边界条件进行非线性快速迭代,求得满足纵向边界的俯仰角指令;
(4)再判断前后制导周期,例如每隔0.2 s的俯仰角指令值之差如果大于设定阈值(如0.5°),就结束纵向迭代按常值俯仰角飞行;否则,随着制导周期的更新,重复上述显式计算过程,循环往复迭代,直到按长半轴关机。
构造的这种控制方法关于偏航角变化的特点是开始以最大偏航角对初始侧向位置和速度偏差进行校正,随着飞行时间的推移,最后阶段逐步向零偏航角靠近,这样偏航通道对纵向通道的耦合影响就非常小了,纵向通道的迭代控制就会很快收敛。制导控制过程如图1所示。

图1 大偏航自适应迭代控制流程图Fig.1 Large yaw self-adaptive combined iterative guidance
2 控制算法
2.1 纵向边界条件的选取
一方面,为方便火箭在发射惯性系中进行制导计算;另一方面,因为大偏航角的耦合造成了纵向平面迭代的强非线性,为保证鲁棒性和确保控制精度,如图2所示,假设入轨时刻k点的地心位置矢量为、速度矢量,当地速度倾角Θk,这里提出采用其标量rk、Vk、Θk,而非土星运载火箭IMG方法采用的直角坐标边界条件,这样不严格限制火箭必须在标准轨道点入轨,而是可准许滑动,这可保证长半轴和偏心率,因为长半轴a和偏心率e与入轨时刻的rk、Vk、Θk直接相关。

图2 纵向边界条件选择Fig.2 Selection of longitudinal boundary conditions

根据式(2)、式(3)可知,如果入轨点的直角坐标参数Xk、Yk与标准关机点的参数不同,但各自的r、V、Θ相同,那么长半轴和偏心率一定相同。所以,在纵平面内运动控制的边界条件是满足标准入轨点对应的地心矢径、速度大小和当地速度倾角

2.2 偏航通道计算公式
偏航通道利用Saturn-5的IMG显式算法:

其中:


式中是标准关机时刻的侧向位置和侧向速度分量;其他参数详见参考文献[2,10]。
2.3 纵向通道公式与耦合补偿修正
纵平面内的迭代控制部分采用LTG方法,先预测纵平面内关机时刻发惯系内的直角坐标参数Xp、p、,然后进一步预测关机时刻的位置矢径rp、速度Vp和当地速度倾角Θp:
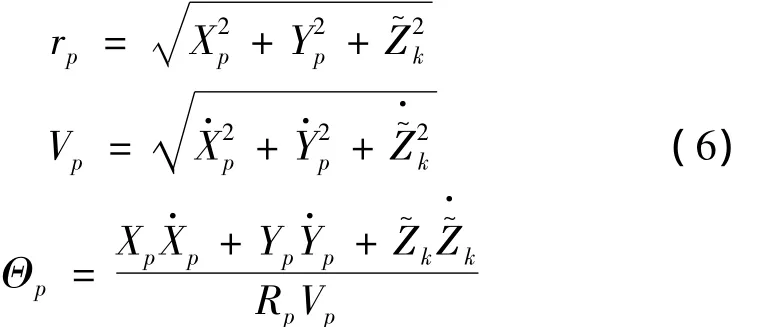
其他纵向通道预测公式参见文献[4-5],不同的是预测式(6)有了修改,而且预测公式中与轴向视加速度aw信号相关的τ,必须考虑大偏航角耦合的影响,如式(7)所示:

式中Ue为有效排气速度;ψ为测量的偏航角。
由LTG方法,发惯系中纵平面内最省燃料推力方向控制律如下:

式中K=Tgo/2;Tgo是剩余飞行时间。
这里提出以变量α、β构造新的二维乘子向量:

其满足LTG控制律的必要条件:两向量正交和¯u是单位向量[4-5],于是只要根据标准轨道初值,按式(10)牛顿迭代公式求出满足边界条件的参数α、β、Tgo,就可求乘子向量,那么推力方向单位向量如式(8)所示 ,记 ¯u=[u(1),u(2)]T,故当前时刻火箭的俯仰姿态角指令如式(11)所示。

这样,式(5)和式(11)分别给出了火箭飞行程序角指令。
2.4 结尾收敛性处理与关机条件
以上算法按给定的制导周期先偏航、后俯仰进行循环往复闭路迭代,若俯仰通道前后2个制导周期的俯仰角之差大于设定阈值(如0.5°),俯仰通道停止迭代,转入常值俯仰角飞行,直到长半轴满足要求关机。
3 仿真验证与比较
以美国“半人马座”火箭的动力参数为例,假设200 km轨道高度分离的初始偏差参数和变轨段推力偏差如表1所示。经过大椭圆滑行,在到达20 000 km高度时刻,要求进行一次性直接入轨控制送入圆轨道,六自由度精度仿真结果如表2所示(这里不涉及导航工具误差,三轴姿态为喷气开关控制)。
2个正负初始偏差组合算例表明,纵向和侧向的初始偏差均较大,特别是经过几个小时的滑行,要实现一次性直接入轨,为抑制初始侧向偏差干扰,正偏差组合算例需要的偏航角幅值为35°,最大负偏差算例需要40°才能完成。从表2看出,大偏航非线性自适应控制方法即算法具有较高的收敛精度,而没有改造的IMG和LTG是发散的。这里给出变轨段正偏差算例的六自由度俯仰偏航姿态曲线如图3、图4所示,可看出正偏差组合算例在偏航角幅值达到35°,入轨控制过程是稳定的。

表1 初始偏差和推力偏差干扰Table 1 Disturbances of initial state and thrust biases

表2 制导控制方法的仿真结果比较Table 2 Comparison of simulation results between guidance methods
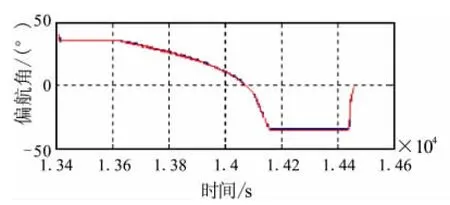
图3 偏航角指令与控制响应曲线Fig.3 Yaw command and control curve

图4 俯仰角指令与控制曲线Fig.4 Pitch command and control curve
4 结论
(1)组合继承了IMG侧向控制律和LTG纵向控制律的优点,纵向通道迭代算法对大偏航角的耦合影响进行了补偿修正,改造了纵向边界条件、迭代算法和结尾自动停止迭代方法。
(2)提高了运载火箭一次性直接入轨的大偏航非线性鲁棒稳定性,使之对侧向大初始偏差和纵向大初始偏差均具有自适应能力,当然对动态干扰如推力偏差和姿控偏差一样具有适应能力。
(3)直接在发惯系中计算,算法方便、简单可靠,可替代IMG和LTG成为一种一般的火箭自适应控制方法,也可适应一次性大异面机动变轨。
[1]Hanson J M,Cruzen M W.Ascent guidance comparisons[R].AIAA 94-3568.
[2]Deniel T Martin,Russell F Sievers,Saturn V guidace.Navigation and targeting[J].J.of Spacecraft,1977,14(7):720-730.
[3]Muratore J F,et al.Space rescue[R].NASA Johnson Space Centre,N20070025530.
[4]Jaggers R F.Multi-stage linear tangent ascent guidance as baselined for the space shuttle[R].NASA-7239,1972.
[5]Daniel Rovner.GN & C for pegasus air-launched space booster:design and first flight results[R].NASA-911105.
[6]Lu Ping.Closed-loop endo-atmospheric ascent guidance[R].AIAA 2002-4558.
[7]Calise A J Lee s.Design and evaluation of a three-dimensional optimal ascent guidance algorithm[J].Journal of Guidance,Control and Dynamics.1998,21(6):867-875.
[8]Gath P F,Calise A J.Optimization of launch vehicle ascent trajectoies with path constraints and coast arcs[J].Journal of Guidance,Control and Dynamics,2001,21(6):296-306.
[9]Strandmoe S,Depasquale E.European ATV flight control achievements[R].AIAA 2008-1214.
[10]韩祝斋.用于大型运载火箭的迭代制导方法[J].宇航学报,1983,4(1):10-16.
[11]茹家欣,等.液体运载火箭的一种迭代制导方法[J].中国科学 E 辑:技术科学,2009,17(4):696-706.
[12]陈新民,余梦伦.迭代制导在运载火箭上的应用研究[J].宇航学报,2003,24(1):10-16.
[13]吴 楠,程文科.运载火箭迭代制导方法的改进[J].动力学与控制学报,2009,7(3):45-51
A robust nonlinear self-adaptive control method with large yaw for rocket orbital insertion
LIU Xin-jian1,YE Cheng-min2,ZHANG Li-jia2,LU Liang-liang2,ZHANG Li-bin2
(1.College of Aerospace and Material Engineering,National University of Defense Technology,Changsha 410073,China;2.Institute of Astronautic System and Engineering,Beijing 100076,China)
Rocket orbital insertion is usually to control flight along standard orbital plane.Common launching mission only requires small yaw correction,but currently some special tasks require rocket be able to fly in power with large lateral yaw guidance to eliminate large initial lateral disturbances to the end-stage rocket orbital insertion.A kind of self-adaptive nonlinear combined guidance method with large yaw was researched and presented for the end-stage rocket orbital insertion,which synthesized the advantages of IMG method of Saturn-V and LTG method of Space Shuttle.The large yaw non-linear coupled compensation was performed and its iterative algorithm of powered flight was modified to improve robust stability.The numerical simulation of six DOF based on attitude nozzle control has demonstrated that the guidance strategy and algorithm are simple,stable and precise,which will be referential and applicable in the rocket orbital insertion and orbital maneuver.
rocket orbital insertion;guidance and control;self-adaptive control;large yaw nonlinear control;space rapid response
V448.1
A
1006-2793(2012)04-0434-04
2012-03-05;
2012-05-11。
航天基金项目(UCS20110518)。
刘新建(1966—),男,博士,研究方向为飞行器设计与控制。E-mail:lxjxyy@126.com
book=4,ebook=242
(编辑:吕耀辉)

