助推－滑翔导弹再入弹道快速优化①

赵 欣，闫循良，张金生，王仕成，何安荣

(1.第二炮兵工程大学，西安 710025;2.第二炮兵驻211厂军代室，北京 100084)

助推－滑翔导弹再入弹道快速优化①

赵 欣1，闫循良1，张金生1，王仕成1，何安荣2

(1.第二炮兵工程大学，西安 710025;2.第二炮兵驻211厂军代室，北京 100084)

基于LGL(Legendre-Gauss-Lobatto)伪谱法，研究了临近空间助推-滑翔导弹再入段弹道快速优化问题。首先，基于改进的气动力模型建立了较为精确的再入数学模型;其次，针对该优化问题在气动数据处理和优化求解上存在的困难，基于LGL伪谱法系统地建立了再入最优飞行弹道的求解步骤，为解决直接利用LGL伪谱法存在的困难，设计了一种基于LGL伪谱法的串行优化求解策略;最后，分别采用积分推进法和协状态映射原理对优化结果进行了可行性和最优性验证。仿真结果表明，本文的弹道优化方法优化1条再入弹道所用时间为3～4 s，计算效率较高，路径约束和端点约束均得到很好满足，算法求解精度较高，有效地实现了多约束多变量大型稀疏的再入弹道导弹快速优化。

临近空间;助推-滑翔导弹;再入弹道优化;伪谱方法;优化控制

0 引言

当前，由于导弹防御系统弹道预测性不断增强，弹道导弹所面临的生存环境越来越恶劣。近些年，为提高导弹的战场生存能力，各军事强国竞相关注并研究中段突防变轨技术［1］，而助推-滑翔导弹正是在这一技术发展中应运而生的新概念武器［2］。助推-滑翔导弹采用升力体形，依靠气动力控制，可在临近空间区域长时间高超声速滑翔飞行，从而实现远程快速攻击，其地位具有深远战略意义。

在临近空间助推-滑翔导弹的研究中，再入弹道优化是系统总体优化中的关键技术之一，它直接影响武器的整体突防性能。然而，由于这类导弹的再入弹道对控制变量高度敏感，且再入过程的非线性约束较强，致使弹道的可行域范围较窄，这决定其再入弹道数值优化存在一定困难［3］。目前，求解弹道优化问题的主流方法有:基于极大值原理的间接法和基于非线性规划理论的直接法［4］。间接法将最优控制问题最终转换为一个两点边值问题［5］，可以获得精确的最优解，但其要求求解状态方程和协态方程，这对于复杂的非线性动力学方程来说较为麻烦，计算量较大;同时，求解过程对共轭变量的初值高度敏感且难以估计，很难收敛，且算法鲁棒性较差。直接法采用参数化方法将连续空间的最优控制问题求解转化为一个非线性规划(Non Linear Programming，NLP)问题，通过数值求解非线性规划问题来获得最优轨迹。与间接法相比，直接法具有以下优点:(1)算法简单、易于理解;(2)对初始值要求不严格，收敛半径大，鲁棒性好;(3)易于处理包含路径约束的最优控制问题［6］。因此，直接法在解决实际问题的适应性上更具有优势。

直接法又可分为2种基本类型:一是离散控制变量(又称直接打靶法)［7］;二是同时离散控制变量和状态变量(又称直接配点法)［8］。前一种方法的主要不足点是节点数目不易确定，取得过少会导致所得到的最优控制解不准确，过多则会增大非线性规划问题的规模，出现“维数灾难”;后一种方法中，一般的直接配点法由于采用分段多项式来近似状态和控制变量时间历程，使得设计变量数目庞大，且初值不易给定，控制曲线不光滑。

近些年发展起来的伪谱法(PSM)开始应用于轨迹优化问题，它也是配点法的一种，它采用全局插值多项式有限基在一系列离散点上近似状态变量和控制变量，相对于一般的配点法，PSM能以较少的节点获得较高的精度［9-10］。同时，采用PSM转化得到的NLP问题的KKT(Karush-Kuhn-Tucker)条件与原最优控制问题一阶最优必要条件的离散形式具有一致性［11］，弥补了一般直接法的不足。上述特点使得PSM成为目前求解复杂最优控制问题最为有效的方法之一。

本文研究Legendre-Gauss-Lobatto(LGL)PSM在临近空间助推-滑翔导弹再入弹道优化中的应用。首先，从工程应用角度出发建立了与真实飞行环境比较相符的临近空间助推-滑翔导弹以再入时间最短为目标的多约束弹道优化模型;在此基础上，采用基于LGL PSM和序列二次规划(SQP)算法的串行优化求解策略处理问题;最后，采用解析法对优化结果进行了可行性和最优性验证。通过仿真对上述方法进行了数值验证。

1 再入弹道优化问题数学模型

所研究问题的数学模型包括再入动力学模型、气动力模型和大气模型。

1.1 再入动力学模型

基于相关假设，考虑地球自转效应，升力式再入飞行器三自由度无量纲动力学方程为

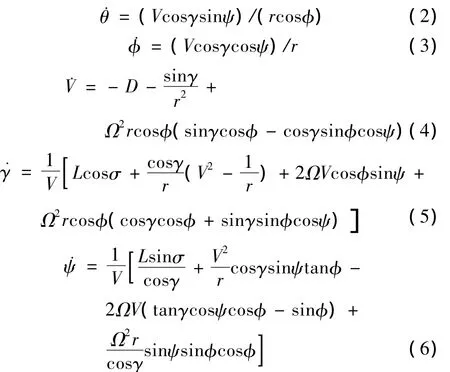
式中r为再入飞行器质心到地球球心的无量纲地心距;θ和φ分别为再入飞行器质心位置的经度和纬度;V为相对地球的无量纲速度;γ为弹道倾角;ψ为速度方位角;Ω为无量纲地球旋转角速度;σ为倾侧角;D和L分别为无量纲的阻力加速度和升力加速度。

1.2 改进的气动力模型

目前，再入轨迹优化中的气动力模型一般采用传统简化形式，即只将气动系数视为攻角函数［3］。然而，实际上气动系数受多种因素的影响，其中攻角α和飞行速度Vm是主要的2个因素，为进一步减小因模型不精确引入的误差，需给出更为精确的气动力模型。文献［12］研究指出，升力系数与攻角近似呈线性关系，与马赫数近似呈负指数变化关系;阻力系数与攻角近似呈二次函数关系，与马赫数也近似呈负指数变化关系。基于此，给出如下的改进的气动力系数模型:

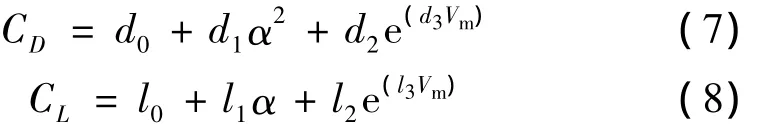
其中，d0、d1、d2、d3、l0、l1、l2、l3均为模型的待辨识参数，本文采用非线性最小二乘法进行辨识。

1.3 大气模型

大气密度模型一般采用1976标准大气模型，该模型为一分段函数，给出了大气密度和声速随高度变化的函数。具体模型见文献［13］。

2 再入弹道优化模型

2.1 再入状态变量和控制变量选择

再入优化问题状态变量为

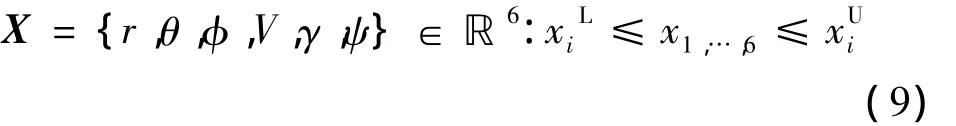
不考虑指令延迟，控制变量可以选择为攻角α和倾侧角σ，因此得到控制空间为

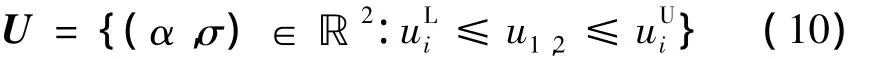
根据以上分析，得到优化变量为(r，θ，φ，V，γ，ψ，α，σ)共8个参数。若设计攻角剖面为马赫数的分段线性函数，则优化控制量只有σ。因此，新的优化变量为(r，θ，φ，V，γ，ψ，σ)，共 7 个参数。

2.2 再入弹道约束

再入飞行过程是一个高动态的过程，需满足一系列苛刻约束条件的限制，如过载限制、动压限制、热流限制和初终端条件限制等。

(1)热流约束

再入热流约束一般是指对飞行器表面驻点处的热流限制，其数学表达式为

驻点热流计算式为

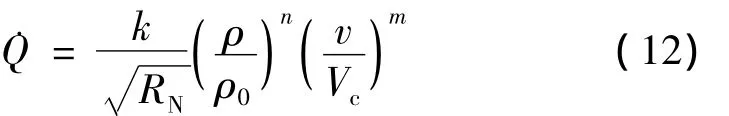
式中 ρ分别为无量纲大气密度;RN为驻点曲率半径;k、ρ0、Vc为常数;v为飞行速度;n由边界层的特性决定，一般情况下把驻点附近的边界层按照层流处理，此时n=1/2;m则需根据气体的粘性等因素来确定，本文取3.25;再入飞行热流限制取=7 000 kW/m2。

(2)过载约束

最大总过载限制主要取决于再入飞行器结构强度和机载设备的可承受过载范围。再入飞行器总过载表达式满足:

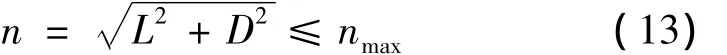
式中nmax为额定最大值，文中取20gn。

(3)动压约束

再入飞行过程中的动压约束一方面取决于随动压增大而增大的气动控制铰链力矩;另一方面取决于飞行器表面防热材料的强度。动压约束为

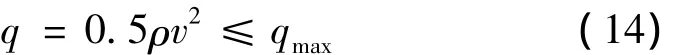
其中qmax为最大动压，文中取qmax=3×105N/m2。

(4)端点条件

再入点初始时刻需满足一定的条件，同时考虑到与末制导段交班的要求，再入终端状态也应满足一定的条件，端点约束条件为

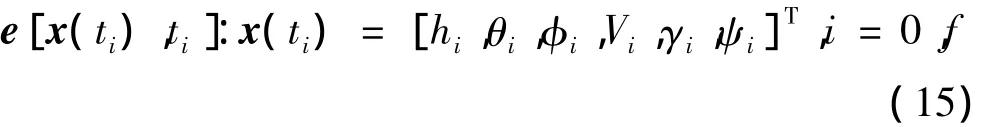
2.3 优化目标函数

对于导弹武器系统而言，再入点和目标点确定后，飞行时间是一个重要指标，即要在尽量短的时间内攻击目标，提高武器的快速打击性能。所以，选取到达目标点飞行时间最短作优化性能指标:

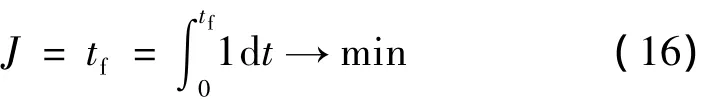
3 基于LGL伪谱法的再入段弹道优化问题求解

3.1 弹道优化问题描述

上述再入弹道优化问题可归纳为以Bolza型为优化目标的非线性最优控制问题:

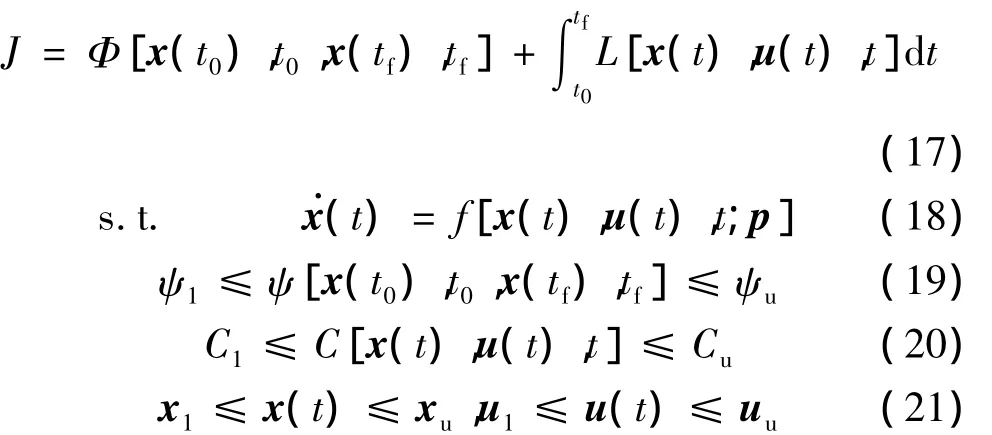
式(17)～式(21)分别对应弹道优化问题的目标函数、动力学方程、边界条件、路径约束、状态量和控制量自身范围约束。

3.2 基于LGL伪谱法弹道优化问题的转化

(1)区间变换处理

轨迹优化问题的时间区间为［t0，tf］，而LGL伪谱法通过τ∈［-1，1］上的拉格朗日多项式拟合控制量和状态量。因此，需将时间区间转换至［-1，1］，最终得到上述最优控制问题的新形式为

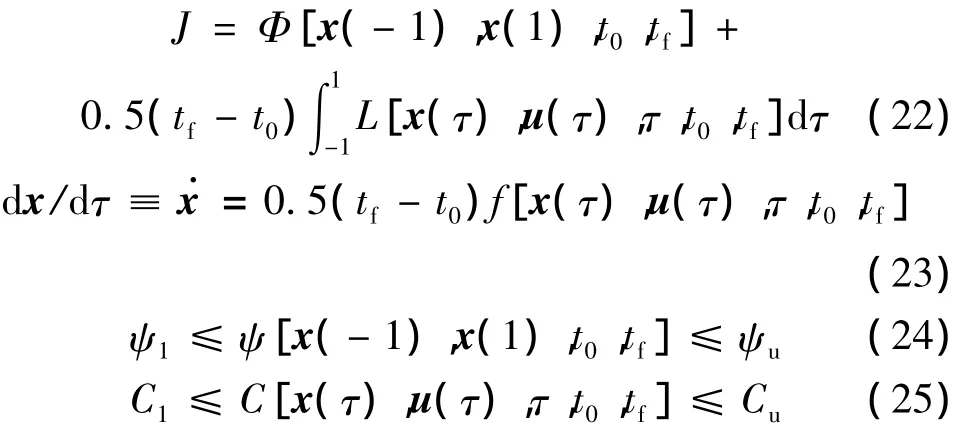
(2)时间区间划分及LGL点

设将时间历程划分为N个子区间，则有N+1个LGL 点 τi(i=0，1，…，N)，其中 τ0=-1，τN= τf=1;中间节点 τi(i=1，2，…，N-1)为N阶 Legendre多项式的导数˙LN的零点。其中，LN为N阶Legendre正交多项式。这些点在［-1，1］上并不是均匀分布的，而是两端密集，中间稀疏，有利于提高拟合精度。

(3)控制变量和状态变量近似

对状态变量和控制变量基于LGL点进行拉格朗日插值近似

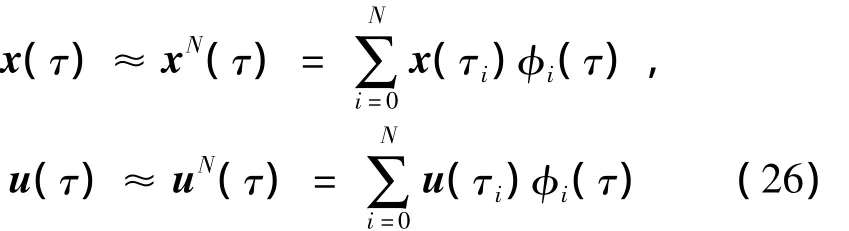
式中 φi(·)为N阶拉格朗日多项式。

在LGL点可得到以下关系式:

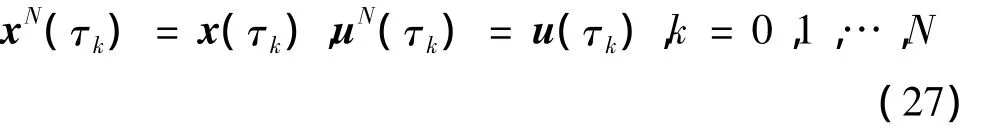
(4)动力学微分方程约束处理

对连续微分约束用插值多项式的微分来代替，对状态近似方程进行微分，在LGL点进行拟合得:

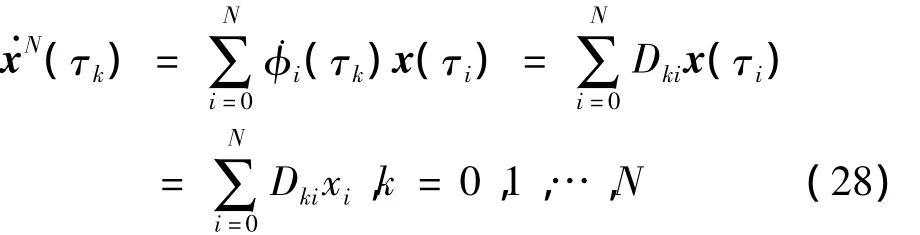
式中Dki为(N+1)×(N+1)阶微分矩阵D的元素。

动力学微分方程约束可近似转换为代数约束，在LGL点拟合得到:

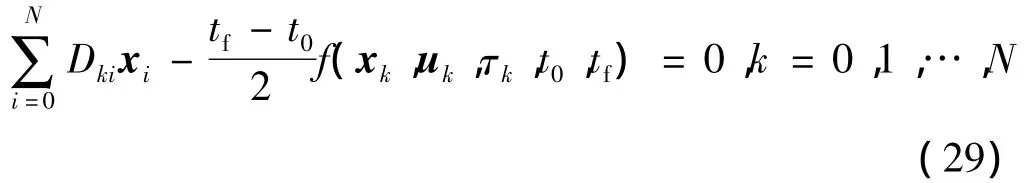
(5)性能指标近似

采用Gauss-Lobatto积分准则对性能指标中的积分项进行数值积分，得到离散的性能指标函数:

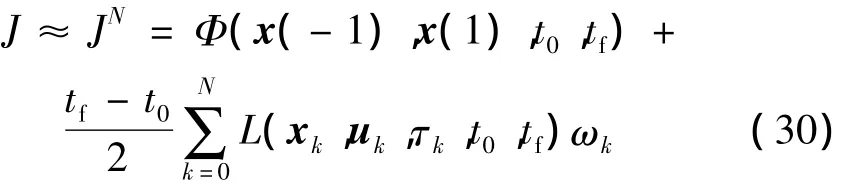
其中，LGL权:

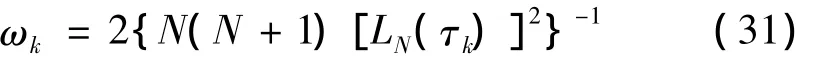
通过以上对最优控制问题在LGL点近似，得到了以下离散化的非线性规划问题，即寻找最优参数X=(x0，x1，…，xN)，U=(u0，u1，…，uN)，t0，tf，使得性能指标JN(X，U)最小化，同时满足代数方程约束、端点约束、路径等约束。其中，优化变量数目为(n+m)(N+1)+2，约束数目为(n+c+m)(N+1)+q。可见，上述离散得到的问题为一大型稀疏NLP问题，对于这类问题的求解，本文采用序列二次规划(SQP)算法，它被认为是目前求NLP问题最有效的方法之一［14］。

3.3 基于LGL伪谱法的串行快速优化策略

理论上，上述LGL伪谱法可直接求解本文研究的问题，然而实际应用中存在以下因难:再入轨迹优化由于状态量和控制量数目较多，如果选取节点数目较多时，优化设计变量的数目将会十分庞大，同时得到的约束方程数目也是非常巨大的，这会大大增加计算负担。另外，对于大范围再入问题，设计变量的初始猜测较为复杂，不恰当的初值会带来计算代价的增加，甚至可能导致问题不收敛或收敛到不可行解。针对再入弹道优化存在的问题，为了提高算法的计算速度及收敛性，本文采用基于LGL伪谱法的串行快速优化策略来进行最优弹道的求解。

(1)设计初值生成器

利用LGL伪谱法能以较少节点获得高精度的优势，先采用较少的节点，计算最优轨迹和最优控制，并以此为下一步精确计算的初值。

(2)采用从可行解到最优解的串行优化策略

串行优化策略是指，不直接找寻满足所有等式约束和不等式约束的解，而是先将等式约束转换为目标函数，将得到的最优解x0作为初值，求解原非线性问题的解。

具体流程:首先，基于从可行解到最优解的策略，由初值生成器获得初值;再选取较多的节点，以求得高精度的最优轨迹和最优控制。

3.4 可行性和最优性验证

为了证明极值解的合理性，研究中进一步完成了优化解的可行性和最优性验证工作。

(1)基于积分推进法的可行性验证

采用积分推进法进行极值解的可行性验证，具体方法:在保证所有约束满足的前提下，利用所得到的控制量，积分推进运动方程得到状态量轨迹，通过比较优化获得的状态量和积分推进得到的状态量轨迹，进行解的可行性验证。如果二者匹配程度在可接受的误差范围内，证明解是可行的。

(2)最优性验证

采用Covector Mapping Principle(CMP)进行一阶最优性验证，即根据庞特里亚金极小值原理，增广哈米尔顿函数 ¯H满足 ∂¯H/∂u=0，将其重新改写，得到控制律的显示表达，将解析得到的控制量与优化得到的控制量进行比较，如果二者是一致的，则一阶最优性是满足的;同时，根据KKT定理可得到相应的补充条件，判断补充条件是否成立，最终实现结果的最优性验证。

4 仿真算例

4.1 再入仿真条件

再入端点条件为

其中，考虑上述初值设定，对应的状态边界条件为

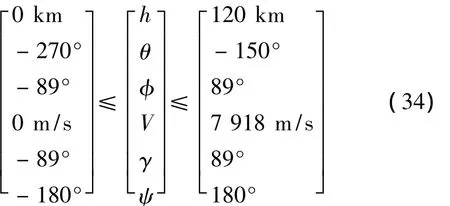
对应的各控制量边界为

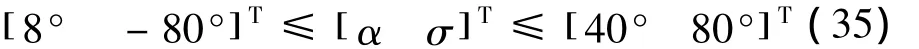
路径约束已经在前文中给出。若设计攻角剖面为马赫数的分段线性函数，即

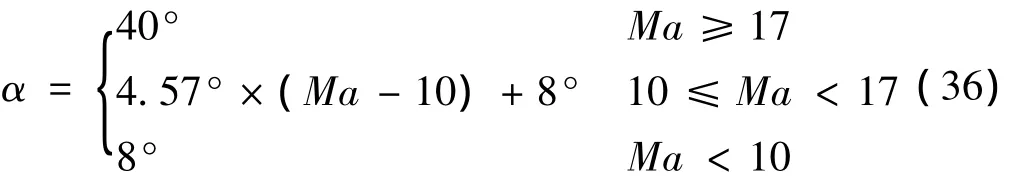
则优化控制量只有σ，因此新的优化变量为(r，θ，φ，γ，ψ，σ)，共7 个参数。

4.2 仿真结果及分析

采用初值生成技术和从可行解到最优解的串行优化技术进行求解。初值生成器中取LGL节点数目为5，则离散化之后得到最终优化变量数目为36，综合考虑各种约束的总约束数目为60。将优化结果作为初值进行多节点优化，选取多节点数目为30，则最终优化变量数目为211，总约束数目为310。

优化需要的目标函数及约束的梯度函数(即雅可比阵)采用解析方法提供。最终，优化指标达到全局最小值为972.93 s，状态量及控制量优化结果如图1～图3所示，各路径约束的约束变量曲线如图4所示。

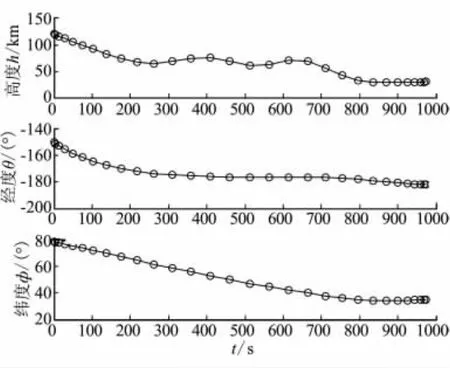
图1 位置变化曲线Fig.1 Curves of position vs time

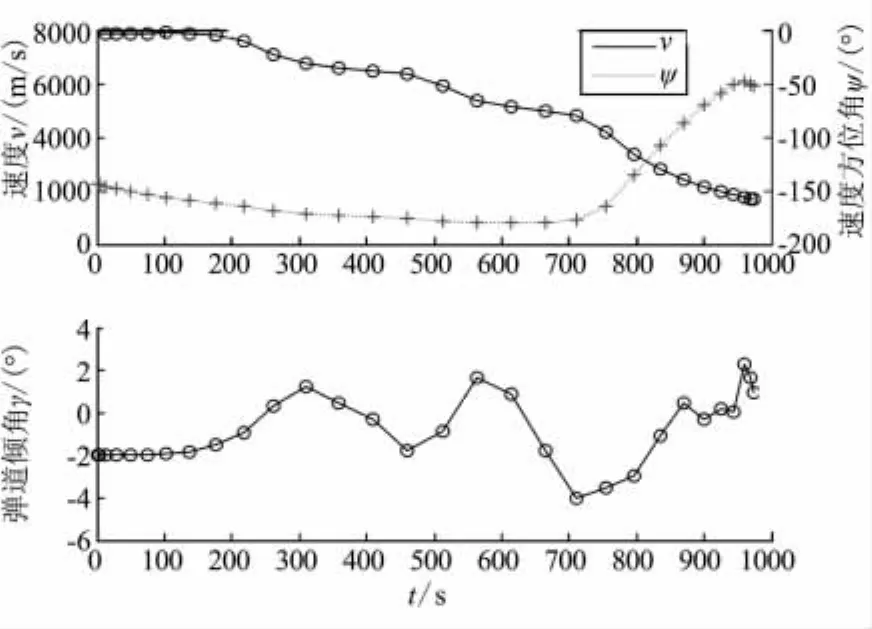
图2 速度相关状态量变化曲线Fig.2 Curves of state variables correlated with velocity vs time

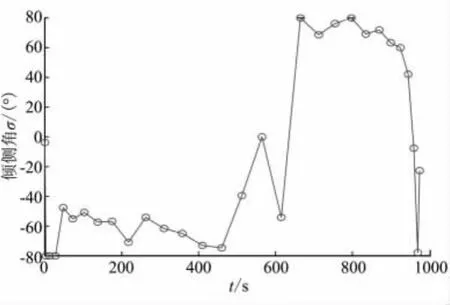
图3 最优控制倾侧角变化曲线Fig.3 Curves of optimal bank angle vs time

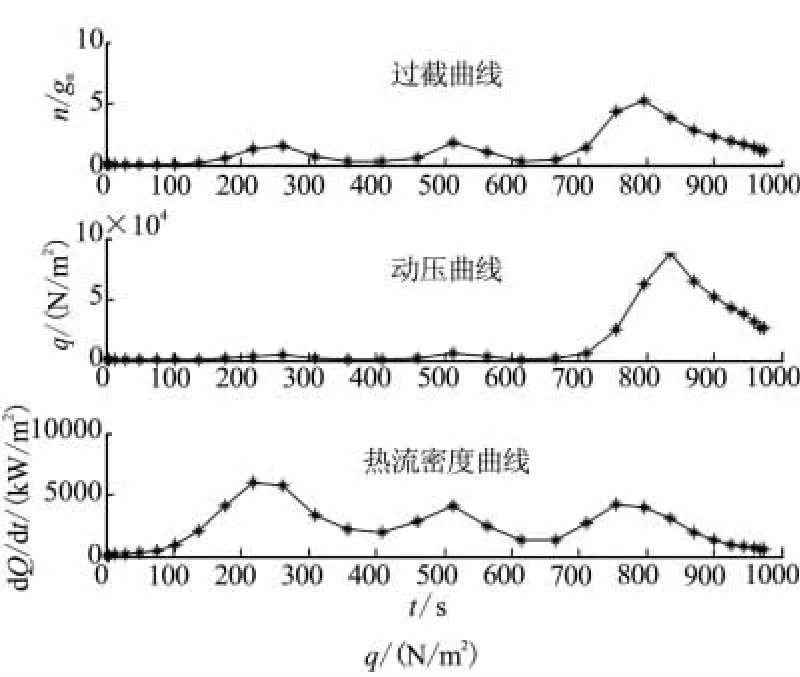
图4 内点路径约束曲线Fig.4 Curves of interior point constraints

优化计算在CPU为E7500/2.93 GHz，2G内存的台式计算机上实现，操作系统为Windows XP。采用MATLAB7.7.0(R2008b)语言进行代码编写，MATLAB环境下进行仿真，SQP算法实现参数优化计算。算例中再入弹道优化的时间包括初值生成时间和精确计算时间两部分，总耗时为3.72 s;直接采用3.2节中的LGL伪谱法，优化计算初值根据再入初始条件和终端条件线性插值简单给出，LGL点个数取30，优化计算所需时间为58.64 s，说明设计的快速优化策略大大提高了优化计算速度。另外，相对于传统优化算法，由于LGL伪谱法不包含积分计算，且离散得到的NLP问题具有典型的稀疏结构。所以，从这两点也可说明这种方法具有较高的计算效率。

另外，相关文献研究指出，若在LINUX环境下，采用C或Fortran语言编写代码，并将代码进一步优化，可使得计算速度提高至少100倍［15］。可见，在计算速度上，利用LGL伪谱法求解助推-滑翔导弹再入弹道优化问题，计算效率较高。

由图1～图4的仿真结果可看出，所得结果满足所有端点约束条件，同时满足各种路径约束，本文建立的优化方法能以较少的节点和计算时间获得状态量的优化解和优化的控制量。

进一步进行可行性验证。将得到的最优控制量σ*(t)进行插值，得到整个时间区间上的σinterp1(t)，采用MATLAB的ode45龙哥库塔积分器，积分推进运动方程可得到状态量推进轨迹，将此结果与本文得到的优化状态量进行对比，得到图5～图7所示结果。

由图5～图7的对比结果可看出，优化结果与推进结果吻合较好，虽然也存在一定的误差，但对于本文所研究的大范围的变轨问题而言，其相对误差(定义为绝对误差/变量值)是较小的，数量级在10-4～10-5左右，说明计算精度较高。即在理想的飞行条件下，临近空间助推-滑翔导弹按照LGL伪谱法获得的最优制导指令进行飞行，可从预定初始点到目标点并实现交接班，从而验证了极值解的可行性。

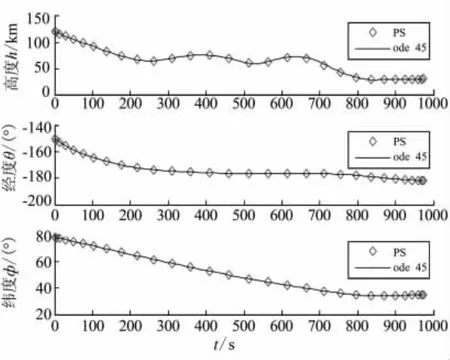
图5 位置比较Fig.5 Comparison of positions

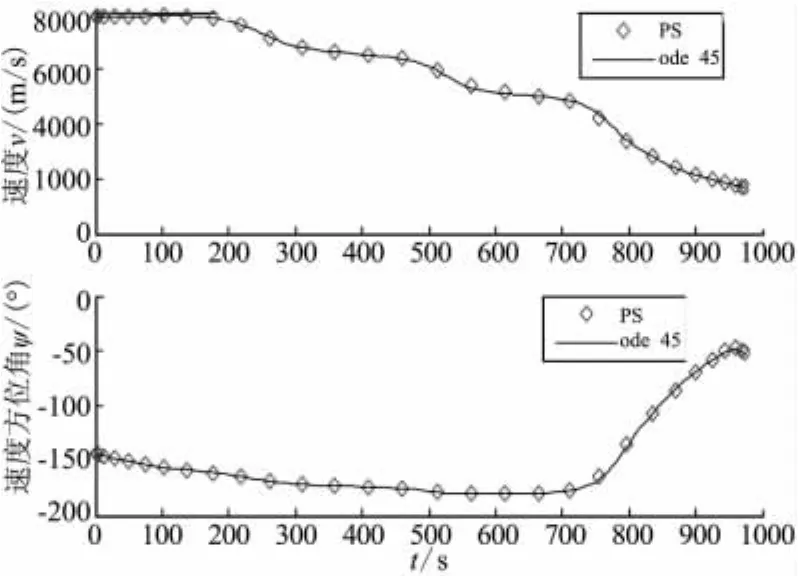
图6 速度及速度方位角比较Fig.6 Comparison of velocity and velocity azimuth

进一步分析偏差存在的原因主要有:

(1)伪谱法离散所选取的LGL节点数目为30，这个点的数目是较少的，要进一步提高精度，必须增加节点数;

(2)由于本文选择倾侧角而不是倾侧角速率作为控制量，这导致无法对倾侧角变化率进行限制，致使倾侧角的变化较为剧烈，而本文采用样条曲线对控制量进行拟合(见图8)，插值所得控制量并不能与优化结果很好地吻合，致使状态量推进结果并不能完全真正地反映最优控制量的作用。

接下来进行最优性验证。本文利用解析法验证问题的一阶最优性，验证原则:Hamiltonian函数沿最优轨线保持为零。采用CMP对协状态进行估计，最终得到该问题的Hamiltonian，如图9所示。可见，通过CMP及解析验证法得到的Hamiltonian在零附近震荡，满足一阶最优性必要条件。

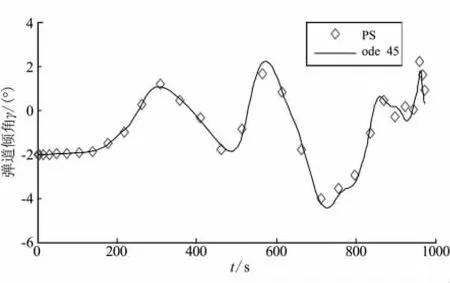
图7 弹道倾角比较Fig.7 Comparison of trajectory obliquity

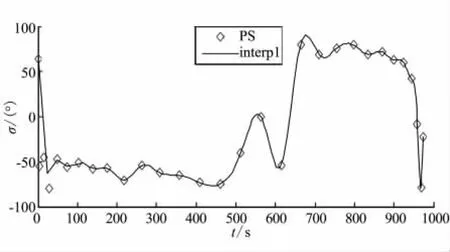
图8 控制量优化结果与插值结果的比较Fig.8 Comparison of optimal result and interpolation result of the controller

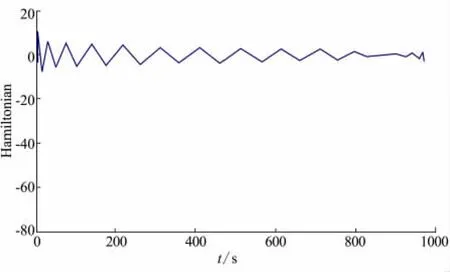
图9 最优控制的HamiltonianFig.9 Hamiltonian of optimal control

同时，给出控制量倾侧角对应的拉格朗日乘子变化曲线，如图10所示。可知，乘子μσ满足KKT定理。因此，极值解的最优性得到了验证。

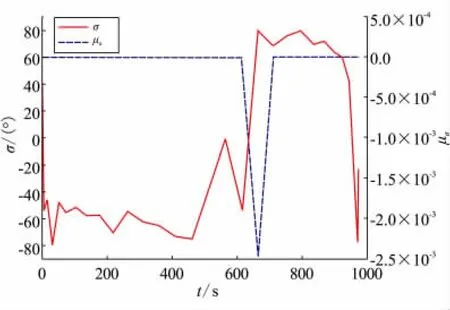
图10 倾侧角与对应的KKT乘子曲线Fig.10 Curves of bank angle and KKT multiplier

5 结论

(1)针对临近空间助推-滑翔导弹再入弹道快速优化问题，建立了多参数、多约束的再入弹道优化模型。

(2)利用LGL伪谱法和SQP相结合的方法详细建立了再入最优飞行弹道的求解步骤，针对直接利用该方法的困难，设计了含初值生成器串行优化求解策略，有效解决了助推-滑翔导弹再入段弹道快速优化问题。仿真结果表明，对于再入弹道的优化求解，LGL伪谱法具有较高的计算效率和计算精度，能够实现多约束、多变量、大型稀疏的再入轨迹快速优化。

(3)完成了极值解的有效性检验，计算分析表明，优化结果满足极小值原理对应的最优性必要条件。

(4)本文的研究成果能提供实时或近实时、开环最优解，可为在线制导、反馈控制的设计提供基本保证。

［1］徐玮，孙丕忠，夏智勋.助推-滑翔导弹总体一体化优化设计［J］.固体火箭技术，2008，31(4):317-320.

［2］李瑜，杨志红，崔乃刚.洲际助推-滑翔导弹全程突防弹道优化［J］.固体火箭技术，2010，33(2):125-130.

［3］陈小庆，侯中喜，刘建霞.高超声速滑翔式飞行器再入轨迹多目标多约束优化［J］.国防科技大学学报，2009，31(6):77-83.

［4］Betts J T.Survey of numerical methods for trajectory optimization［J］.Journal of Guidance，Control，and Dynamics，1998，21(2):193-207.

［5］Gergaud J，Haberkorn T.Orbital transfer:some links between the low thrust and the impulse cases［J］.Acta Astronautica，2007，60:649-657.

［6］Hui T L，Ping Y J，Qun F，et al.Reentry skipping trajectory optimization usingdirectparameteroptimization method［C］//14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference，2006.

［7］Gao Y，Li W Q.Systematic direct approach for optimizing continuous-thrust earth-orbit transfers［J］.Journal of Aeronautics，2009，22:56-69.

［8］Desai P N，Conway B A.Six-degree-of-freedom trajectory optimization using a two-timescale collocation architecture［J］.Journal of Guidance，Control，and Dynamics，2008，31(5):1308-1315.

［9］Geoffrey T Huntington，David Benson，Anil V Rao.A comparison of accuracy and computational efficiency of three pseudospectral methods［R］.AIAA 2007-6405.

［10］Bemon A，Thorvaldsen T，Rao V.Direct tmjectory optimization and costae estimation via an orthogonal collocation method［J］.Journal of Guidance，Control，and Dynamics，2006，29(6):1435-1440.

［11］杨希祥，张为华.基于Gauss伪谱法的固体运载火箭上升段轨迹快速优化研究［J］.宇航学报，2011，32(1):15-21.

［12］孙勇，段广仁，张卯瑞，等.高超声速飞行器再入过程改进气动系统模型［J］.系统工程与电子技术，2011，33(1):134-137.

［13］Etkin B，Reid L D.Dynamics of flight-stability and control［M］.New York:John Wiley and Sons lnc，1995.

［14］Philip E G.SNOPT:an SQP algorithm for large-scale constrained optimization［J］.SIAM Review，2005，47(1):99-131.

［15］闫循良.基于空间发射的组合机动路径规划研究［D］.西安:西北工业大学，2011.

Rapid re-entry trajectory optimization for boost-glide missile

ZHAO Xin1，YAN Xun-liang1，ZHANG Jin-sheng1，WANG Shi-cheng1，HE An-rong2
(1.The Second Artillery Engineering University，Xi＇an 710025，China;2.The Military Deputy office of the Second Artillery in 211 Factory，Beijing 100084，China)

Rapid re-entry trajectory optimization of near space boost-glide missile was studied via the Legendre-Gauss-Lobatto(LGL)pseudospectral method.Firstly，an accurate mathematics model in re-entry phase was established based on an improved aerodynamic model.Aiming at the difficulties of the optimization problem in processing of aerodynamic data as well as optimization solving，the steps based on LGL pseudospectral method were listed systemically for solving the optimal re-entry flight trajectory.Then a serial strategy based on LGL pseudospectral method was presented to deal with the difficulties in optimization using the LGL pseudospectral method directly.Finally，the feasibility and the optimality of optimal result were validated by integral propagation method and covector mapping principle，respectively.Simulation results show that computational time required for optimizing one reentry trajectory is 3 ～4 s，and thus the computational efficiency is high.Path constrains and boundary constrains are well satisfied，and the precision of this trajectory optimization method is high.The rapid re-entry trajectory optimization with characteristics of multiple constraints，multiple variables and large sparsity is achieved.

near space;boost-glide missile;re-entry trajectory optimization;pseudospectral method;optimal control

V448.2

A

1006-2793(2012)04-0427-07

2012-04-09;

2012-07-09。

国家自然科学基金项目(60874093);863项目(2011AA7053016)。

赵欣(1984—)，男，博士，研究方向为飞行动力学及控制。E-mail:zhaoxin20062111@163.com

(编辑:崔贤彬)