复杂防雷条件下保护范围及三维模型研究
王枫红, 陈炽坤
(华南理工大学设计学院,广东 广州 510640)
在实际防雷工作中,有很多建筑物采用了多种防雷设施结合的手段。这种复杂条件下的防雷设计给防雷保护范围及其三维模型的研究带来了一定的困难[1]。目前,关于复杂防雷模型的研究还比较少见,本文将以复杂防雷条件下的保护范围及其三维模型为研究对象,探讨其生成方法。
1 复杂防雷现状
如果建筑物高度高于滚球半径时,单靠避雷针几乎起不到什么效果,还可能发生雷电绕击现象。并且单支避雷针的保护范围并不是同针高的增减成正比例,只有在接近地面的情况下,保护范围的半径才处于最大值,随着高度的增加,保护范围的半径缩小速度反而增快;另外,在同等高度处,不同高度的避雷针的保护范围半径相差并不大[2]。因此,在选择防雷设计方案时,并不是避雷针高度越高越好。合理配置的两支20m的避雷针在某高度的保护范围要比 40m避雷针的保护范围大。
一般情况下,如果屋顶安装有避雷带、避雷线、接地金属等相对经济的接闪器,则这些设施可以起到地平面或基准面的作用,则只需安置高度较低的避雷针,就可获得较大的保护范围。另外,还有其他因素影响防雷保护范围。防雷设计中建筑物附近突出的其它建筑物、树木、山等也可在不同程度上充当避雷针或基准面(地面)的角色[3]。这些因素将会对防雷效果产生较大影响,因此,在防雷设计中必须予以认真考虑。
综上所述,本文所要研究的复杂模型是在多种防雷设施结合应用下,综合考虑建筑物所处环境的防雷保护范围模型。在多种因素作用下,我们不可能简单的利用单针、多针防雷范围的方法确定保护范围,必须另辟蹊径。
2 保护范围平面二维轮廓线的求取
2.1 由轮廓线重建模型的思路
尽管复杂条件下的防雷模型需另辟蹊径,但仍然适用滚球法。滚球在装有接闪器的建筑物上滚过时,滚球体在受到建筑物上安装之接闪器的阻挡时,无法触及某些区域,这个区域范围就是接闪器的保护范围。根据这一原则就可以得出滚球球心的运动轨迹,如图1所示。复杂防雷条件下的保护范围模型相对要复杂得多。以图2为例,避雷针旁的建筑物顶安装有接闪器,滚球球心轨迹为曲线 C1、C2、C3,其中曲线 C1、C2与曲线C3分布在不同的高度平面上。
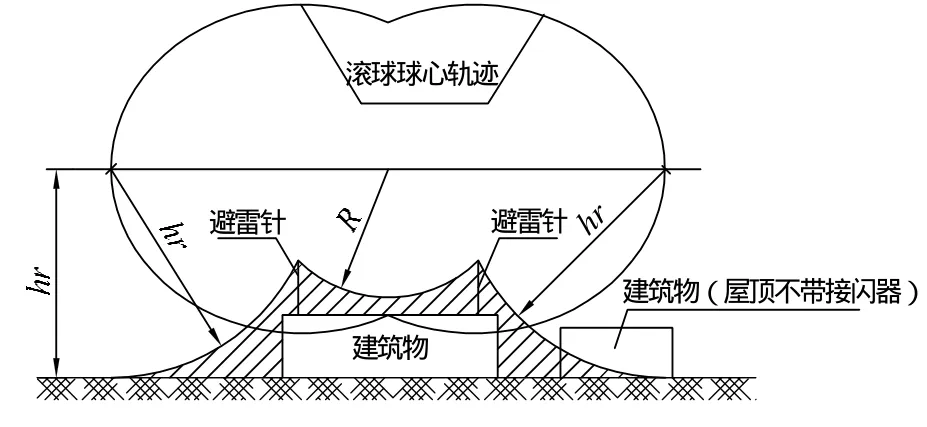
图1 简单防雷模型滚球球心运动轨迹
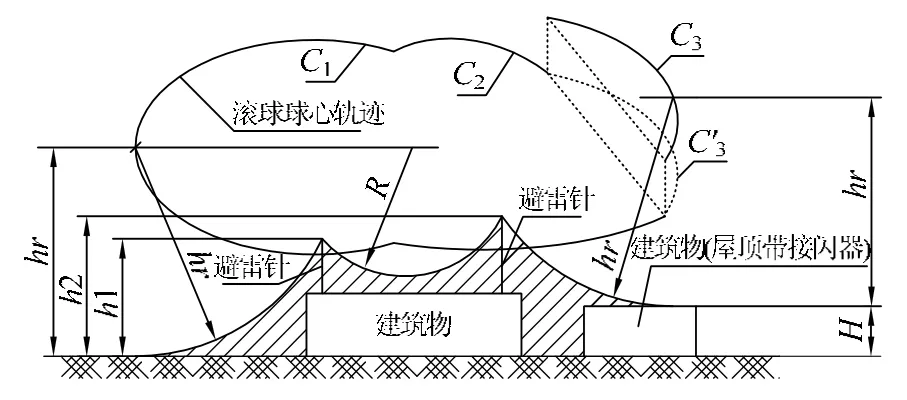
图2 复杂防雷模型滚球球心运动轨迹
显然复杂防雷条件下的模型可以从滚球法的原理中找到研究的思路。当一定半径的圆在某高度平面上沿着滚球球心运动轨迹运动时,所形成之图形将形成内包络线,该包络线就是在这一高度平面上保护范围的截面图形和轮廓线。以此类推,可得到不同高度平面上的轮廓线或等高线。可以利用这些不同高度上的轮廓线或等高线进行三角剖分,建立防雷保护范围的三维模型。
2.2 保护范围轮廓线的产生及实现
2.2.1 复杂防雷条件下的滚球轨迹
如图2所示,有双支不等高避雷针旁的建筑物顶有接闪器为例,在该图中曲线 C1、C2、C3为球心轨迹曲线,其中对曲线C2和曲线C3连接处做了简化处理(主要是因为C2与C3不是处于同一高度,两曲线之间的连接曲线很复杂,而防雷又是个对精确没有过严要求的设计),曲线C'3为曲线C3在曲线C1、C2所在平面的投影图。根据图2所描述的球心运动轨迹可以看出,球心的运动轨迹比较简单、规则,是由多条圆弧或直线连接所组成。圆弧 C1、C2、C3可由如下方程来描述
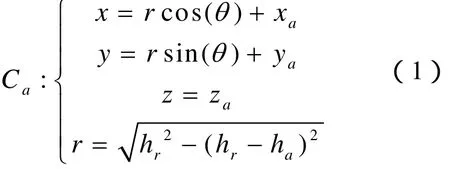
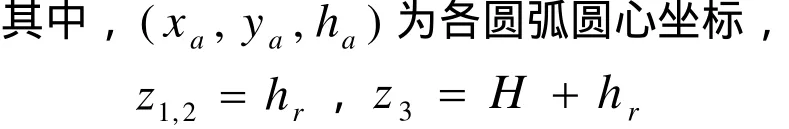
ha为避雷针的针顶与地面或屋顶的接闪器等基准面间的距离,h1、h2分别取避雷针1和2的针高,h3= h2- H。
2.2.2 截面轮廓线的数学模型及实现研究
当滚球在轨迹上运动时,其在某高度平面上的截面就是无数的圆在运动,由这些圆形成的内包络线就是防雷保护范围的平面轮廓线。
1)包络原理
根据滚球球心轨迹方程式1知,由于各圆弧圆心坐标已知,该方程为参数θ的函数,同时该方程也是各曲线簇(在本文中为圆簇)的运动轨迹函数,即为单参数的曲线簇。
对于单参数平面曲线簇,其方程为{Ca}: F(x,y, z)=0,当a取某个实数值时,就得到一条确定的簇中曲线Ca。如果存在一条平面曲线L,它的每一点至少和簇中一条曲线相切,并且L与簇中每一条曲线至少切于一点,则称L为曲线簇{Ca}的包络线[4]。
如图3所示,和曲线簇中每一根曲线同时都相切的一根曲线叫做包络线L。对包络线上的每一点,必然能找到与包络线在此点相切的簇中的一根曲线。即曲线簇中的一根曲线上至少有一点落在包络线上并与包络线相切,包络线就是由这无数的切点所组成。这无数的切点既在曲线簇上、又在包络线上。所以曲线簇的方程式C适合于包络线L的方程式。

图3 包络原理图

代入第1式,即可获得包络线L的表达式 F(x, y,a(x, y))=0。
2)保护范围平面轮廓线的获取
图4为复杂防雷条件下滚球球心运动轨迹图(以双支不等高避雷针为例),为获得不同高度平面上的防雷保护范围的轮廓线,需将球心轨迹投影到该平面上。
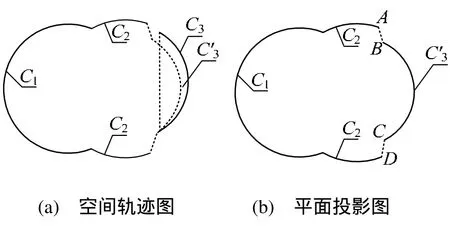
图4 球心轨迹图
图4(b)为球心轨迹在某高度平面上的投影。由于空间曲线 C2、C3间的连接曲线较复杂,而防雷保护范围设计的精度要求不是太高,因此笔者对空间曲线 C2、C3在某高度平面上的投影曲线 C2、C'3之间的连接曲线做了简化处理。以直线AB和CD连接,得出球心轨迹投影后的曲线C1、C2、C'3。在获取滚球球心轨迹在某高度平面上的投影曲线后,将按一定规律、一定半径的曲线簇(本文取为圆簇)沿轨迹曲线运动,所形成的内包络曲线就是该高度平面上的保护范围轮廓线。图4(b)中的曲线由两部分组成:曲线C1与C2圆簇半径相同,设圆簇半径为r'1;曲线C'3为不同半径的另一圆簇,设圆簇半径为r'2。
图5为各圆簇半径的计算方法。其中:
曲线C1与C2处的圆簇半径为

在不同高度平面上,按上文规定的圆簇半径方法,若干圆在球心轨迹上运动,所形成图形的内包络线即为在这些高度上的防雷范围的轮廓线,在曲线 C2、C'3的连接处应用包络原理获得的图形按图6所示的方法处理。
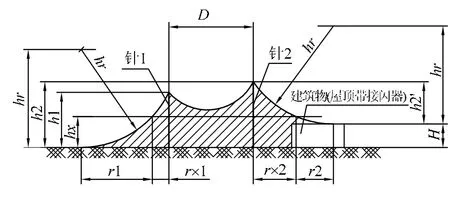
图5 不同高度平面上的rx
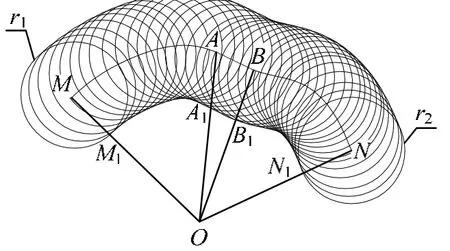
图6 内包络线的处理方法
图6中由滚球轨迹曲线AOM产生的内包络线为弧A1OM1,由滚球轨迹曲线BON产生的内包络线为弧B1ON1,连接直线A1B1,即为内包络线A1OM1和B1ON1的连接线。之所以如此简化处理,是因为直线A1B1相比附近圆簇更靠近内侧,也就是说使该部分保护范围轮廓线向内缩了,因此导致保护范围也略微变小,这就使得保护设计更严格了,不会影响防雷设计的安全性。
根据以上方法获得的轮廓线可用以下方程表示
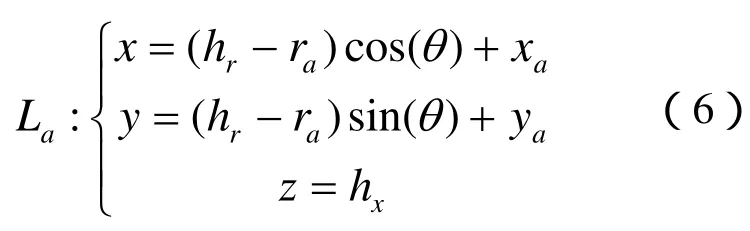
其中ra按式(4)和式(5)确定。通过这3个方程就可以建立轮廓线的数学模型。
3)轮廓线的对应问题
为使各相邻断层上的轮廓线具有几何形状上的相似性,我们可以用一种简单的轮廓线相对位置的约束方法,即判断两相邻断层上的轮廓线中心点距离是否充分小。令j 和 j+1层上的两条轮廓线分别为和,它们之间的距离定义为

其中dj是两层轮廓线之间的垂直距离,是轮廓线区域内的面积,是轮廓线区域内的面积,函数 g计算x∈到轮廓线中所有内点的最短欧氏距离。
在轮廓线的对应问题上,除了单轮廓线对单轮廓线外,还有单轮廓线对多轮廓线、多轮廓线对多轮廓线的问题。而多轮廓不仅涉及到层间轮廓线的对应问题,还涉及到该平面多轮廓线间的三角剖分问题[5]。本文研究的防雷保护模型的轮廓线均为简单对应的曲线,不存在复杂轮廓的对应问题,因此轮廓对应问题对本章研究的影响不大。
4)轮廓线的实现
根据前面介绍的包络线的数学模型,获取轮廓线如图7所示,图中的外围粗线条为滚球球心轨迹在轮廓线平面上的投影线,内侧的粗线条为保护范围的轮廓线。

图7 应用包络原理求取轮廓线
3 二维轮廓线重构三维模型的实现
3.1 重构方法
断层间三角面片表面几何重建技术的研究已相当成熟,其中最短对角线法是一种计算量小、计算速度较快的优化方法。本研究采用最短对角线法作为三角面片生成的优化方法[5]。该方法就是在四边形P1P2QlQ2中的两条对角线P1Q2和P2Q1中,选择较短的一条对角线作为下一个三角面片的边,生成三角面片,如图8所示。通过一系列相互连接的三角面片将上、下两条轮廓线连接起来,以此完成三维形体表面重构。
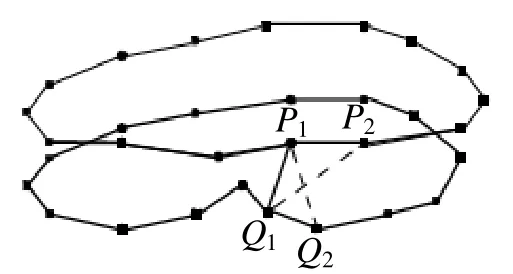
图8 最短对角线法示意图
按以上断层模型生成的方法,对N个断层按顺序做层间四面体连接,得到N-1层四面体,叠加所有四面体层就可以形成三维实体的四面体网格。
3.2 仿真实验
本文以两支相距10m、高度为10m的等高避雷针保护范围的设计为例,完成了该保护范围模型的表面形体重建,如图9所示。

图9 仿真应用实例
图9(a)为通过三角划分形成的避雷针保护范围的表面网格图示,图9(b)是由三角面片形成的保护范围的表面。由于时间有限,本文只以较为粗糙的精度实现了简单双支等高避雷针的表面重建工作,高精度的三角划分和体重构工作还有待进一步研究和实现。
4 结 论
复杂防雷条件下的防雷保护范围的求取对于三维模型的创建至关重要。本文提出采用滚球法,并基于包络线法的不同高度的防雷轮廓线求解方法,研究了通过二维轮廓线重建三维模型的方法。由二维轮廓线重建保护范围模型的方案不仅适合于复杂条件的防雷范围设计,同样也适合简单模型条件下的防雷范围模型,为防雷保护范围设计提供了一条新的思路。
[1]夏文光, 陈堂勇. 建筑物及电子信息系统防雷设计探讨[J]. 电气应用, 2008, 27(3): 30-32.
[2]GIVT21431一2008, 建筑物防雷装置检测技术规范[S].
[3]廖科成. 建筑物幕墙防雷施工技术探讨[J]. 低压电器, 2008, 22: 43-47.
[4]Zhang Hui, Huang Yongqiang. Envelope filtering algorithm and its application in image denoising [D].Guangzou:Sun Yat-Sen University, 2008.
[5]姚民仓, 秦新强, 胡 钢. 基于包络线法的不同树种叶片高光谱特征分析[J]. 微计算机信息, 2009, 25:214-216.

