基于Hough变换的三次方Bezier曲线检测算法研究

孙文赟， 韩 斌

（江苏科技大学电气与信息工程学院，江苏 张家港 215600）

经典Hough变换[1]常用于直线（段）、圆（弧）、椭圆和抛物线的检测，Ballard[2]提出的广义Hough变换(Generalized Hough Transform，简称GHT)可用于检测任意形状，随后出现了大量对GHT的改进，文献[3-4]使用对偶点方法降低GHT的复杂度，文献[5]使用模糊推论系统提高GHT的精确度。在应用方面，文献[6]提出一种改进型广义 Hough变换并用于茄子果实位姿识别。

Bezier曲线于1962年由Pierre Bezier发现并用于汽车设计，是目前计算机图形学中相当重要的参数曲线，也应用于工程图纸和测量曲线的矢量化等领域[7-8]。

在GHT的基础上，本文针对Bezier曲线的特点，提出了一种使用 Hough变换的三次方Bezier曲线检测算法。只需给出待检测三次方Bezier曲线的大致绘制图案，算法根据所给出的待检图形的数字图像建立曲线模型，然后在复杂图像中检测该形状曲线出现的位置、大小和方向。算法由待检图形建模和曲线检测两个部分组成。

1 待检曲线建模

1.1 点阵图像的矢量化

所需检测曲线图像是像素点阵图，需将其矢量化以便用于检测，目前已经有一些关于点阵图矢量化的研究成果[9]，并投入应用领域。这些算法大多使用最小二乘法拟合曲线，其中，文献[9]提出的算法具有代表性。该算法首先提取模板图像的骨架并使用八方向链码的方法追踪曲线，得到规格点序列 {Qi|i= 0,1,2…n-1}。使用最小二乘 法 对{Qi}拟合使Qi=(Xi,Yi)的 均 方 误 差 最 小 ， 求 出d0,d1,d2,d3。最终三次方Bezier曲线的4个控制点由公式计算得到。

1.2 待检曲线的规格化

本文将待检Bezier曲线规格化，以使得其具有平移、缩放和旋转不变特征。

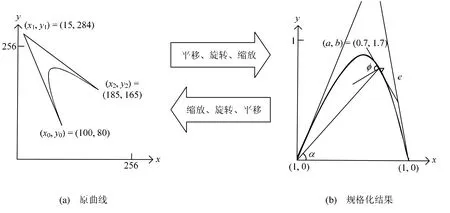
图1 二次方Bezier曲线

定义1 将二次方Bezier曲线经过平移、旋转、缩放，使首尾的两个控制点为(0,0)和(0,1)，中间控制点(a,b)即反映了原曲线的形状特征，称此变换为Bezier曲线的规格化。

二次方 Bezier曲线的规格化及其逆变换的计算方法为

其中：R()、S()、T()为标准旋转缩放、平移变换

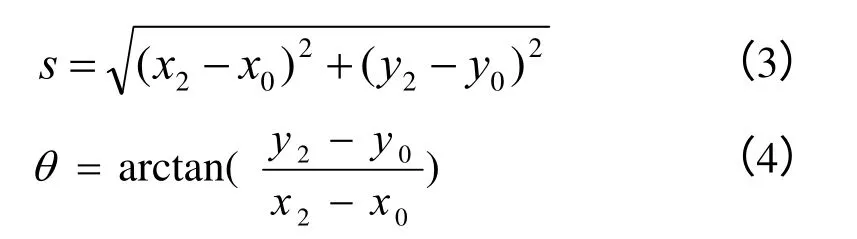
二次方Bezier曲线的形状特征

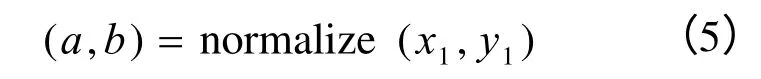
三次方的情况类似，使用首末两个控制点确定变换的形式，第2、第3两个控制点经变换得到(a,b)、(c,d)表示圆曲线的形状特征。

2 曲线检测

2.1 R函数

图1(b)所示的规格化Bezier曲线，边缘点到参考点的距离|r|与边缘点到参考点连线交切线的夹角φ有确定关系

式(6)即R函数。R函数不受平移、缩放、旋转影响，仅由形状决定，是曲线特征的另一种表示方式，使用R函数可以方便地确定参考点，且比原本曲线特征参数表示简便、规范。所以，我们需先将待检测的图形转换成R函数表示。

规格化三次方Bezier曲线对应的R函数的计算方法及其推导过程如下：

三次方Bezier曲线的参数方程为

整理得关于t的三次多项式

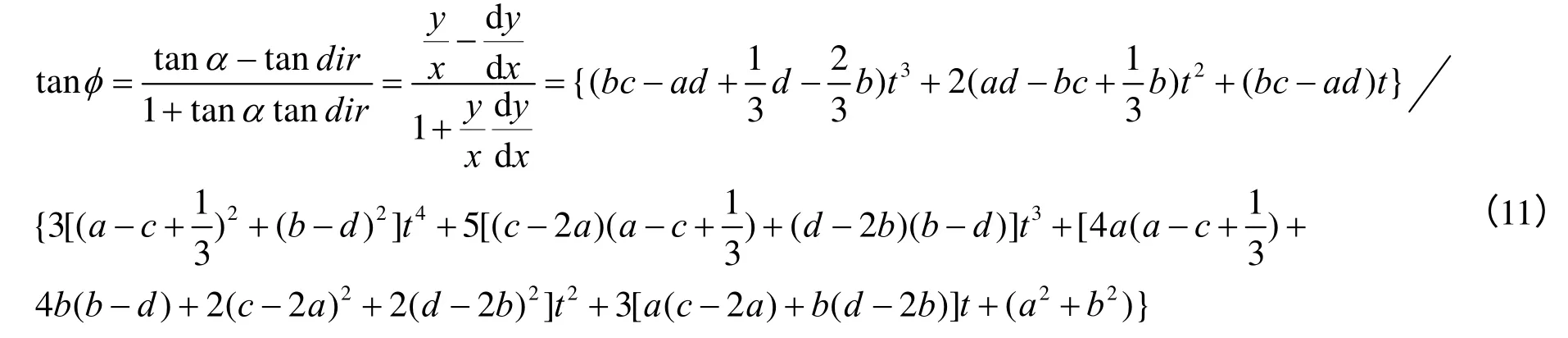
整理得关于t的四次方程

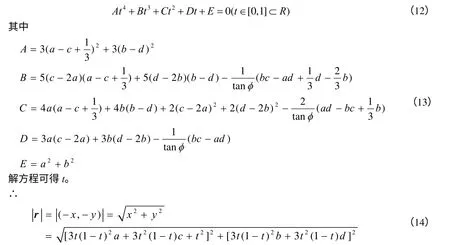
此即为式(6)所对应的R函数。

2.2 使用R函数的Hough变换

与所有Hough变换算法类似，本文算法的主要思想是先投票再统计：使用一个三维累加器数组A，对于每个边缘点尝试各种s和φ，通过R函数求得参考点可能的位置，对其投票，所有投票结束后统计最大值，最大值所在位置即(x0,y0)、s。投票部分的伪代码为：

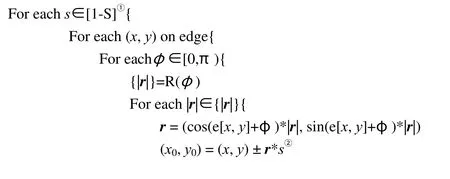
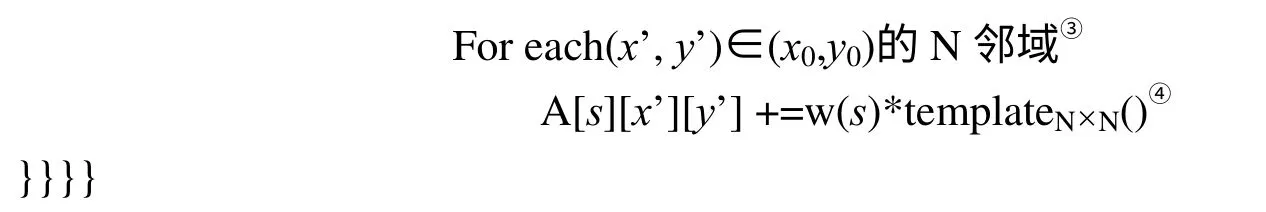
上述伪代码中：

①处S为曲线大小s的最大值，从规格化曲线的定义可知，曲线的大小为其在图像中初始点和终止点的距离，所以s≤S≤图像对角线长度。

②处使用±是无法避免的，这是因为边缘方向有二义性，可以理解为一对相差π的角度，从而导致推测的参考点不唯一。

③处使用模糊模板进行投票，以克服输入图像噪声干扰和输入方向不精确的问题[5]。templateN×N(i,j)为宽度为N的正方形模板，理想的模板是二维高斯函数

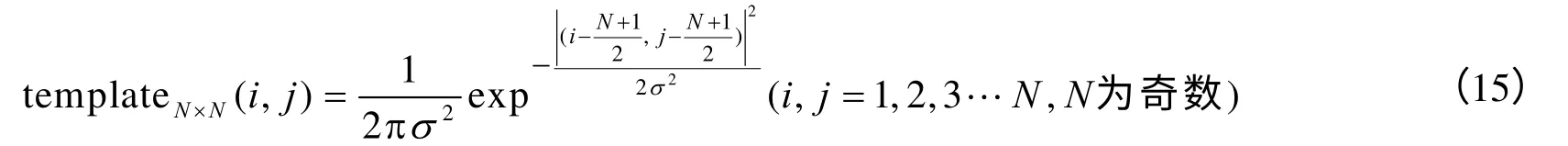
当s变化时，投票点靠近／远离边缘点，投票点的误差随之变小／变大，调整窗口的大小，以适应不同情况，窗口的大小可按下式计算

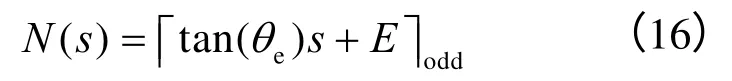
其中，θe是允许的误差夹角，较小时可取tan(θe)≈θe，常数E为曲线位置可能存在的绝对误差，表示向上取奇数操作。

④处使用一个关于s的增函数w(s)作为投票权值调节因子，解决当s较小时投票的集中程度大，影响判断的问题，经多次实验调整，取w(s)=s0.7625合适。

③、④两处可先用A[s][x0][y0]++替代，待投票完成后对累加器A中各层进行平滑滤波并调节权值，从而避免大量浮点数累加，降低算法复杂度，且结果不变。

Hough投票的时间、空间复杂度分别为

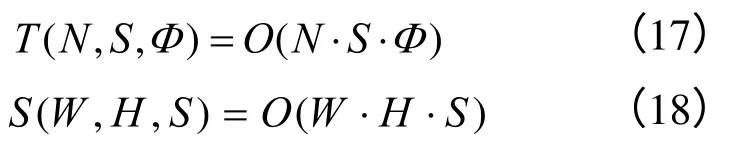
其中，W、H为长宽，N为边缘点数量，S为曲线大小s的最大值，Φ为角度分割数量。这也是整个算法的时间、空间复杂度。

Hough变换利用曲线边缘方向忽视其自身旋转，降低Hough空间的维数，达到减少存储空间并降低计算量的目的，但带来的曲线方向无法直接求出其副作用。

2.3 计算曲线方向

在已知曲线特征、位置和大小的基础上，使用模糊匹配法求其方向。使用一个一维累加器数组B，对已知(x0,y0)、s的Bezier曲线尝试不同的旋转角度，“绘制”空间域上假设曲线，使用一个中心元素最大、外围元素较小的窗口在假设曲线上滑动，与实际曲线进行模糊比较，并根据吻合程度对当前角度投票，所有投票结束后统计最大值，其位置即θ。

关于θ的投票数是所有在对应假设曲线上的滑动窗口的吻合程度总和，即

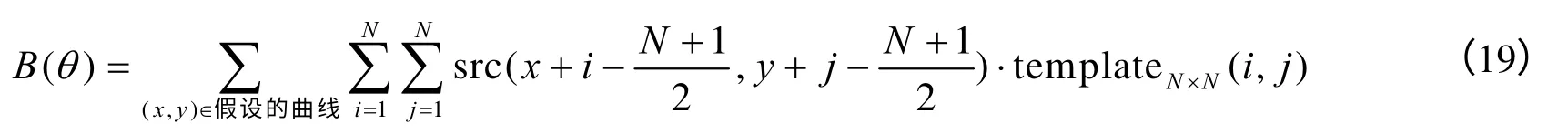
窗口模板的取值方法与前文相同。当窗口靠近或远离参考点(x0,y0)时，调整窗口的大小N，使得所有窗口可以恰好覆盖实际曲线可能存在的圆形区域，窗口的宽度的取值为

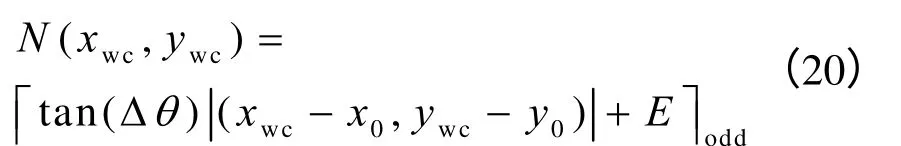
其中，(xwc,ywc)是窗口的中心位置，常数Δθ为角度变化的步长，较小时可取 tan(Δθ)≈ Δθ。

3 实验结果与分析

本文选用尺寸为800×600的机械制图扫描图像进行三次方Bezier曲线检测算法的实验，编写程序对其进行若干步骤的处理，得到了正确结果。

实验步骤的数据流程图如图2所示，首先提取扫描图像的边缘并裁剪某个曲线部分，提取曲线特征得到各种参数，根据形状参数使用此算法在图中找出曲线的位置、大小和角度。结果表明，算法的误差在允许的范围内。

使用GHT方法，建立大小为100的离散R表代替连续的R函数，其它保持不变，得到另一组结果，对比表1中两种方法，本文改进方法的精确度优于GHT方法。

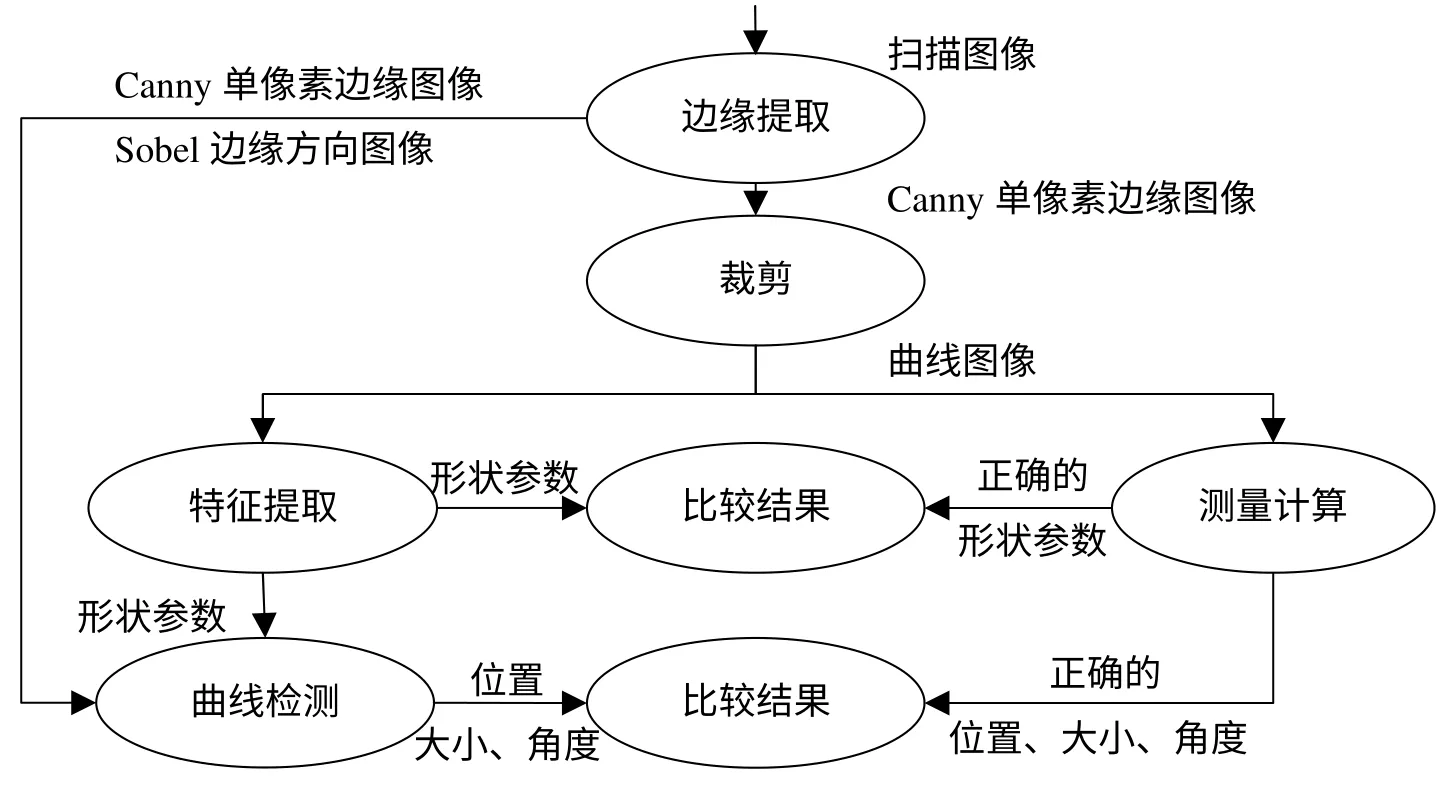
图2 实验步骤的数据流程图

表1 实验结果数据

4 结 论

广义Hough变换[2]中使用到的R表与本文的R函数类似，区别在于：（1）R表使用采样的方法记录离散、有限的边缘点到参考点的关系；（2）R表存储的是r向量，本文R函数仅返回其模值。和广义 Hough变换相比，本文算法对特征的描述更加精确，广义 Hough变换方法可以检测包括Bezier曲线在内的任意形状，但当边缘像素和参考点的距离较远时，临近边缘像素的φ近似，查表法将会得到相同的r，最终导致对参考点的投票分散，而本文使用比R表精确的R函数方法不会出现这类问题。

[1]Hough P V C. Method and means for recognizing complex patterns: U S, 3069654 [P]. 1962-12-18.

[2]Ballard D H. Generalizing the hough transform to detect arbitrary shapes [J]. Pattern Recognition, 1982,13: 111-122.

[3]Ser P K, Siu W C. Non-analytic object recognition using the hough transform with the matching technique [J]. Computers and Digital Techniques, 1994,141(1): 11-16.

[4]刘宏申, 程 健, 高尚义. 对偶点广义 Hough变换算法的改进[J]. 计算机工程与设计, 2009, 30(2):423-425.

[5]Izadinia H, Sadeghi F, Ebadzadeh M M. Fuzzy generalized hough transform invariant to rotation and scale in noisy environment [C]//Proceedings of the 18th International Conference on Fuzzy Systems.Piscataway NJ, USA: IEEE Press, 2009: 153-158.

[6]姚立健, 丁为民, 张培培, 等. 基于改进型广义Hough 变换的茄子果实位姿识别方法[J]. 农业工程学报, 2009, 25(12): 128-132.

[7]Yuan Huaqiang, Ye Yangdong, Deng Jianguang, et al.A fingerprint feature extraction algorithm based on curvature of Bezier curve [J]. Progress in Natural Science, 2007, 17(11): 1376-1381.

[8]殷明霞, 刘群辉, 桂幸民. 利用Bezier样条曲线进行叶轮机可视化设计[J]. 航空动力学报, 2006, 21(1):156-160.

[9]余学军, 彭立中. 二值图像曲线轮廓提取的新算法[J].中国图象图形学报, 2002, 7A(3): 272-275.