基于干扰观测器的卫星姿态误差四元数模糊滑模控制

穆朝絮 孙长银 钱承山，2

(1东南大学自动化学院，南京210096)

(2南京信息工程大学信息与控制学院，南京210044)

卫星在执行特定任务时，对飞行姿态有一定的要求，如要求对地观测卫星的观测仪器窗口始终对准地面.因此，对卫星进行姿态控制是卫星技术发展的关键.传统的以欧拉角描述航天器姿态的控制方法具有直接明确的几何意义，但需要进行大量的三角函数计算，且在进行大角度(如俯仰角为±π/2)机动调整时会出现奇异现象.采用四元数方法描述卫星姿态，能解决上述奇异性问题且有利于存贮和计算.文献［1］设计了四元数反馈控制律，有效地解决了飞行器大角度姿态控制问题.近年来，四元数方法在航天器姿态定位与控制中得到了广泛应用［2-4］.然而，四元数描述卫星姿态具有双值性.文献［5］采用误差四元数方法描述航天器姿态，解决了姿态控制中最终姿态表示的非单值问题.

滑模控制是处理非线性系统控制问题的一种有效方法.它对外部扰动具有良好的鲁棒性，在航天器控制系统中得到了广泛的应用［6-10］.文献［6-9］讨论了滑模控制在卫星姿态稳定控制中的应用.对于外界干扰，滑模控制是通过使用高控制增益来获得鲁棒性的，因而对执行机构提出了较高的要求，有时甚至是无法实现的，亦会加剧抖振的幅值.近年来，干扰观测器方法受到普遍关注.该方法的优点是能够有效克服外界干扰但不需要高的控制器增益.文献［10］针对卫星姿态控制问题设计了滑模控制律，并基于状态方程设计了干扰观测器，以抑制滑模控制中固有的抖振，提高控制效果，但是该方法要求干扰信号的导数为零，仅对慢时变干扰信号有效.

本文以基于误差四元数和误差角速度的卫星动力学方程和运动学方程为研究对象，采用Lyapunov方法设计了一种滑模控制器.通过引入干扰观测器来消减干扰的影响，并构造了模糊规则平滑控制量.对卫星姿态系统的仿真结果表明，所设计的控制方案在实现卫星姿态控制的同时，有效解决了滑模控制的抖振问题，且具有良好的鲁棒性.

1 卫星姿态系统的数学模型

1.1 基于四元数的卫星姿态系统模型

刚体卫星姿态动力学方程为

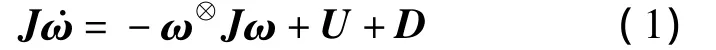
式中，ω=［ω1ω2ω3］T∈R3为卫星本体坐标系相对于惯性坐标系的角速度矢量;J∈R3×3为卫星的转动惯量矩阵，且为正定矩阵;U=［u1u2u3］T∈R3为三轴控制力矩矢量;D∈R3为系统的干扰力矩;对于∀ω∈R3，符号ω⊗可表示为

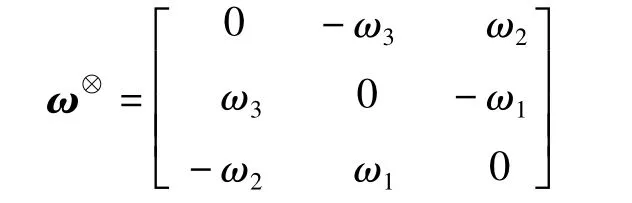
刚体卫星姿态运动学方程应用四元数法可表示为

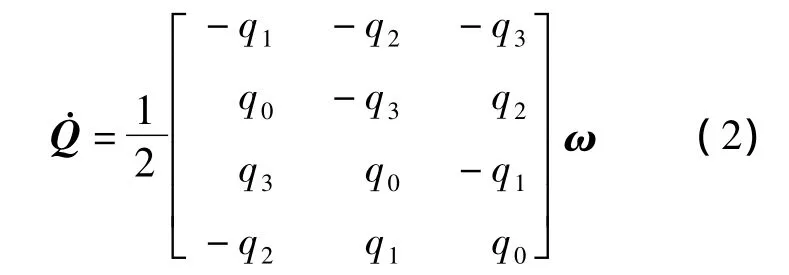
式中，Q=［q0q1q2q3］T为卫星本体坐标系相对惯性坐标系的旋转四元数矢量，且满足

1.2 基于误差四元数的卫星姿态系统模型

考虑三轴稳定的卫星姿态控制，以轨道坐标系作为参考坐标系.设轨道坐标系到惯性坐标系的目标姿态四元数 Qc=［qc0qc1qc2qc3］T，系统初始姿态四元数Q=［q0q1q2q3］T，则卫星本体坐标系到轨道坐标系的姿态误差四元数Qe定义为

在偏航角、滚转角、俯仰角均为0的条件下，设卫星目标姿态四元数Qc= [1 0 00]T.由式(3)可知，系统误差四元数与系统初始姿态四元数相同.对于跟踪问题，可以证明，当Qc=±Q时，Qe=0，即+Q和－Q表示的位置是相同的，采用四元数±Q表示航空器姿态具有双值性，但用误差四元数Qe表示时则具有单值性.Qe=0表示卫星达到所要求的姿态位置，这是采用误差四元数描述航天器姿态运动的优点.

设ωc=［ωc1ωc2ωc3］T为轨道坐标系的目标姿态角速度，ωe=［ωe1ωe2ωe3］T为卫星本体坐标系相对于轨道坐标系的误差角速度，则

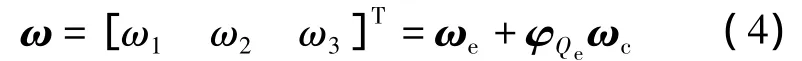
式中，φQe为由误差四元数Qe描述的从轨道坐标系到卫星本体坐标系的姿态旋转矩阵，且

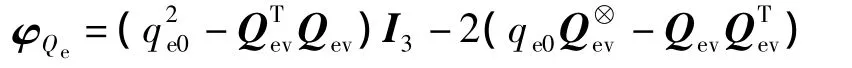
根据式(1)、(2)和(4)，可得基于误差四元数的卫星动力学方程和运动学方程，即

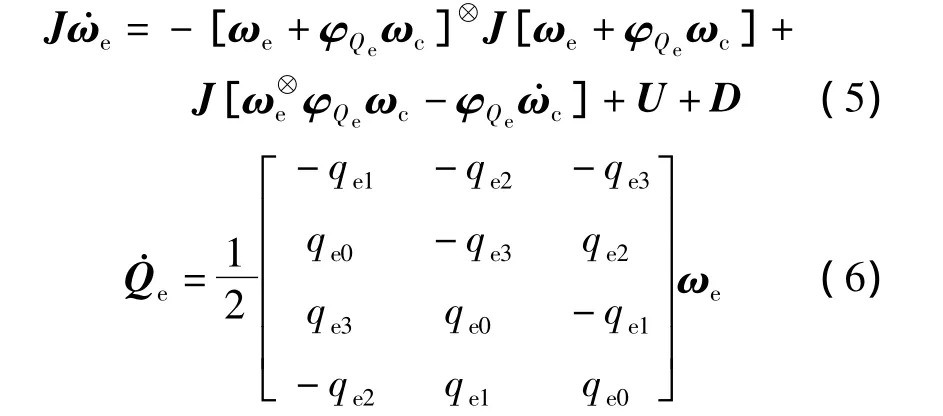
式中，D(t)=［d1(t)d2(t)d3(t)］T，且‖d1(t)‖，其中均为常数.

因此，欲将卫星三轴姿态惯性定向于某个位置，只须设计适当的滑模控制器U即可，使得式(5)和(6)描述的闭环系统渐近稳定，并满足

2 基于干扰观测器的卫星模糊滑模控制器设计

2.1 卫星姿态系统滑模控制器设计

在滑模控制中，通过设计控制律，可使被控系统在有限时间内到达预先设计的滑模面，并沿滑模面以适当的速度渐近趋向平衡点.

考察式(5)和(6)描述的闭环系统，定义系统滑模面为

式中，S=［s1s2s3］T∈R3为滑模变量;K=diag(k1，k2，k3)，且 kj＞0，j=1，2，3.

定理1针对式(5)和(6)描述的非线性动态系统，在干扰有界的条件下，取滑模控制律为

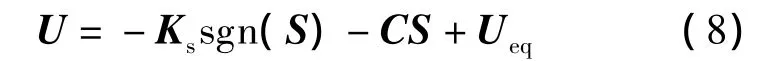
式中，C，Ks为正定对角矩阵，且 Ks＞L1，其中 L1=为等效控制量;sgn(S)=［sgn(s1)sgn(s2)sgn(s3)］T为符号函数.则系统状态ωe和Qev能在有限时间到达滑模面S，并沿滑模面渐近收敛至原点.

证明选取Lyapunov函数，则

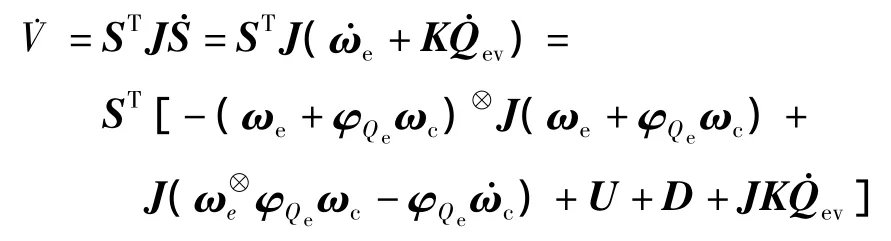
等效控制Ueq设计为

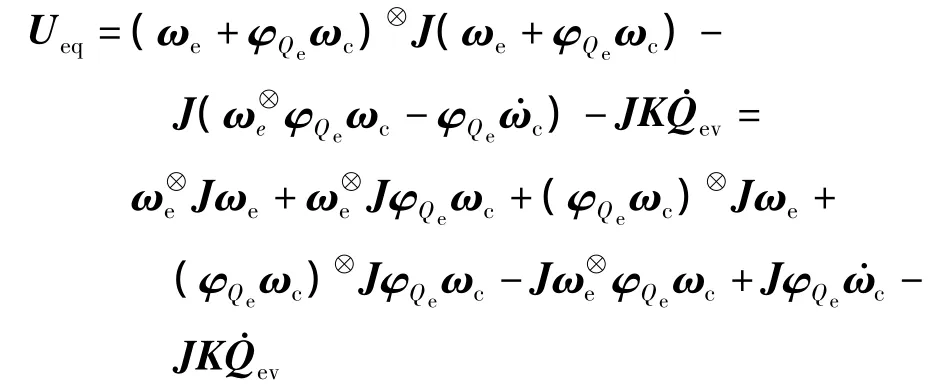
将滑模控制律U=－Kssgn(S)－CS+Ueq代入，且K's=Ks－L1，则

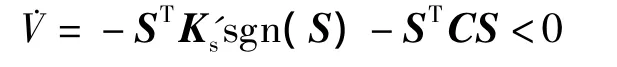
故系统状态ωe和Qev可以在有限时间内到达滑模面S.

当系统状态到达滑模面时，S=0，系统将在U=Ueq作用下沿滑模面运动.若S＞0，则控制量U＜Ueq，相当于产生负的控制力矩将系统状态控制到滑模面;若S＜0，则控制量U＞Ueq，相当于产生正的控制力矩将系统状态控制到滑模面.

系统状态在滑模面上时，S=0，即 ωe=－KQev，代入式(6)可得，在滑模面上Qev满足形如的动态方程.为了简化证明，设kj=k，则渐近到达原点.由于 ωe与Qev成比例关系，则ωe也渐近到达平衡点.证毕.

2.2 干扰观测器的设计

依据文献［11-12］中提出的微分器算法，得到如下引理.

引理1对于函数p(t)，若其n阶导数是李普希兹连续的，且李普希兹常数为L，则

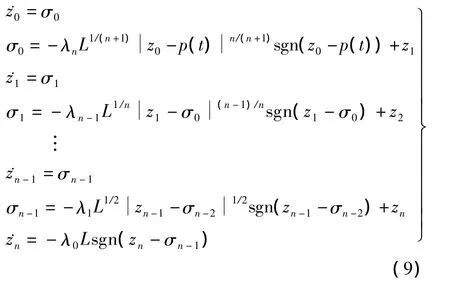
式中，z0，z1，…，zn分别为的估计;λi(i=0，1，…，n)为微分器增益.

为了保证微分器的收敛，增益λi需要足够大.文献［11］已证明了对于任意阶次的形如式(9)的微分器都存在一组增益序列{λi}ni=0，使得式(9)在有限时间内收敛.对于一个5阶的微分器，增益可以取为 λ0=1.1，λ1=1.5，λ2=2，λ3=3，λ4=5，λ5=8.

考虑如下的一阶系统:

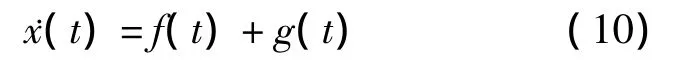
式中，x(t)∈R，f(t)∈R分别为已知的状态和变量;g(t)∈R为有界未知干扰.

根据引理1，由干扰g(t)设计的干扰观测器具有如下定理.

定理2对于形如式(10)的非线性系统，‖g(t)‖＜L，其估计值可以由下式获得:

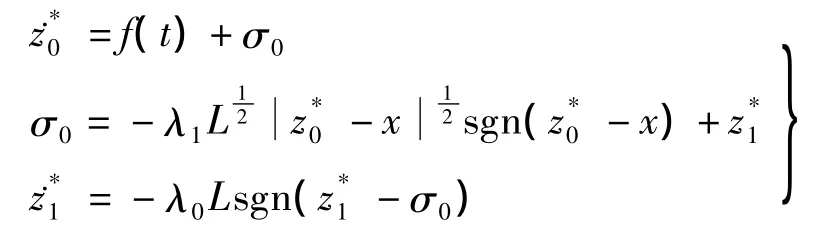
证明根据引理1，设微分器输入为

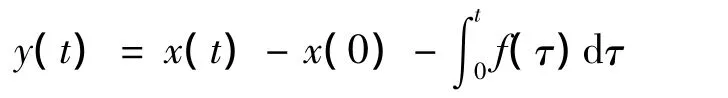
取一阶微分器为

由微分器原理可知，z1将在有限时间内收敛到)(即g(t)).

故

由此可知，对于g(t)，存在如下形式的干扰观测器:

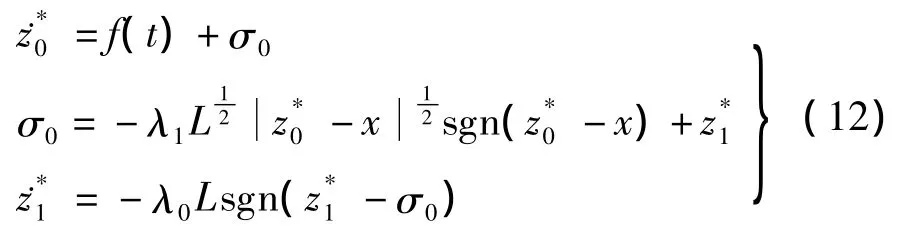
式中，λ0=1.1;λ1=1.5.将在有限时间内收敛到g(t).证毕.

考虑到ωe与干扰的关系，式(5)中的干扰可改写为G(t)=J－1D(t)=［g1(t)g2(t)g3(t)］T.G(t)有界，则，其中为常数.又设J－1U，x=ωe，则G(t)的干扰观测器可按下式设计:

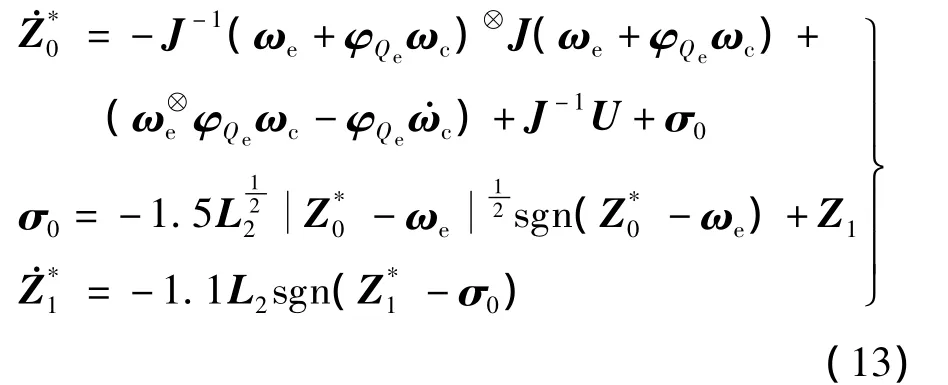
基于干扰观测器的卫星误差四元数姿态控制动力学方程为

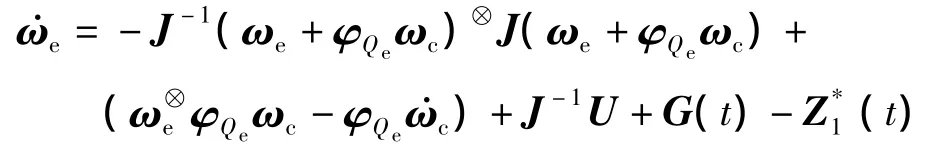
2.3 模糊化

模糊控制算法由模糊化、模糊逻辑规则推理和解模糊化组成.在本文所设计的卫星模糊滑模姿态控制系统中，采用sj作为模糊推理系统的输入变量为输出变量，具体设计算法步骤如下:

①确定输入、输出变量论域，定义输入、输出变量的模糊语言值分别为

②采用如表1所示的模糊推理规则进行推理.

表1 模糊推理规则

③采用重心法将模糊输出精确化.

3 仿真算例及分析

下面利用本文设计的干扰观测器估计卫星受到的干扰，然后设计模糊滑模控制律，对卫星姿态控制系统进行仿真实验.在仿真的初始条件中，卫星转动惯量为

目标姿态角速度为

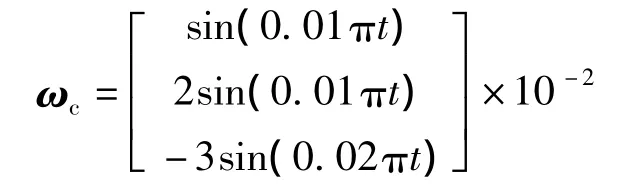
外界未知干扰力矩为

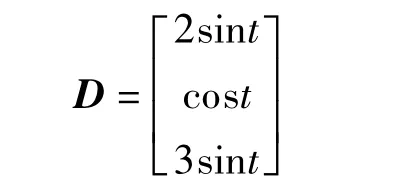
卫星初始误差姿态为

卫星初始误差角速度为

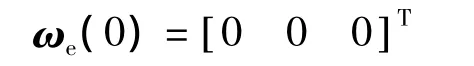
滑模控制器参数为

按照误差四元数方法对卫星的姿态系统进行建模，基于干扰观测器设计滑模控制律，在上述初始条件下，干扰观测器参数设计为λ0=1.1，λ1=1.5，L2=diag(0.02，0.01，0.03).干扰观测器对误差的估计曲线和观测误差如图1所示.基于干扰观测器的滑模控制下系统的误差角速度以及常规滑模控制下系统的误差角速度如图2所示.

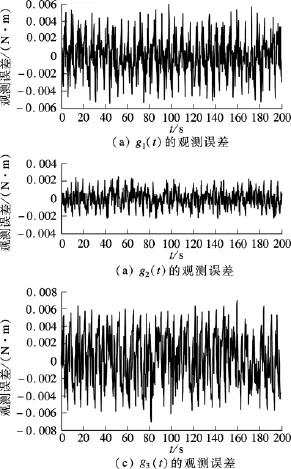
图1 干扰观测器对干扰的估计

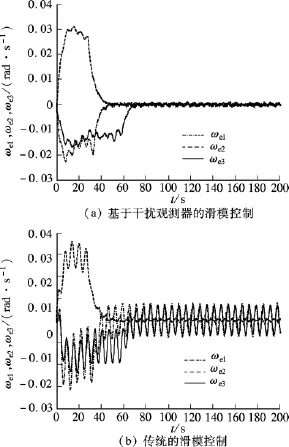
图2 2种控制下姿态角速度的误差变化曲线

在 Ks=diag(1，1，1)，C=diag(2，2，2)的增益条件下，使用干扰观测器的滑模控制较好地减弱了未知干扰对系统的影响，使用较小的控制增益便可让系统达到渐近稳定的状态.然而，由于干扰的影响，在较小的控制增益下，传统的滑模控制不能使系统稳定.由于高频切换，基于干扰补偿的滑模控制闭环系统出现了抖振，这不利于控制器的实际使用，控制效果也不理想.为此，根据滑模量sj的大小，通过模糊逻辑推理直接设计~ksj，以代替不连续的符号函数，构成模糊滑模控制律.

在模糊滑模控制器设计中，输入论域为［－0.1，0.1］，输出论域为［－125，125］.图 3 ～图5分别给出了模糊滑模控制下误差四元数和误差角速度曲线、姿态角速度跟踪曲线以及模糊滑模控制量输出曲线.由图可知，对于给定的大角度初始条件，卫星的误差姿态四元数和误差姿态角速度以较高的精度达到目标值，姿态角也较好地跟踪了目标姿态角，控制过程中抖振被抑制，姿态控制系统性能良好.滑模控制抖振情况已经获得了明显的改善.

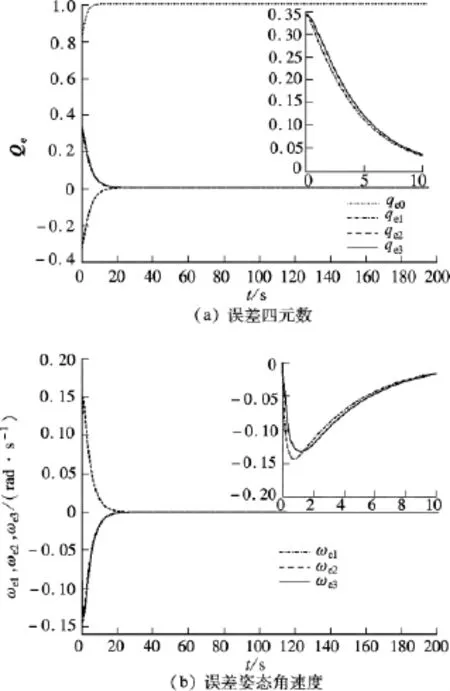
图3 模糊滑模控制下误差角速度和误差四元数曲线

图4 模糊滑模控制下姿态角速度跟踪曲线

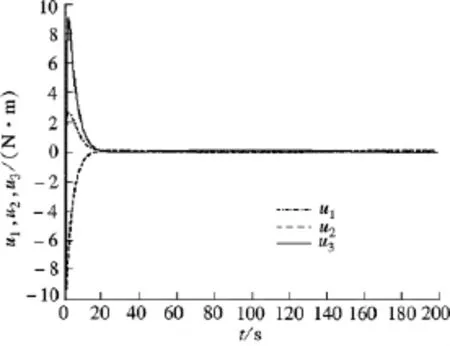
图5 模糊滑模控制量输出曲线

4 结语

本文采用误差四元数的卫星姿态描述方法，设计了基于干扰观测器的误差四元数卫星姿态模糊滑模控制器.该方法能够实时估计未知干扰，减小控制器的输出幅值;引入模糊方法设计切换项，可在不降低鲁棒性的前提下，有效抑制滑模控制中存在的抖振问题.仿真验证结果证明，本文所提的卫星姿态控制方法能有效地达到控制目标，控制性能良好.

References)

［1］Bilimoria K D，Wie B.Time-optimal three axis reorientation of a rigid spacecraft［J］.Journal of Guidance，Control and Dynamics，1993，16(3):446-452.

［2］Hecht C.Homing guidance using angular acceleration of the line of sight［C］//Processing of the AIAA Guidance，Navigation and Control Conference.New Orleans，LA，USA，1991:856-869.

［3］Robinettr P G.Spacecraft Euler parameter tracking of large-angle maneuvers via sliding mode control［J］.Journal of Guidance，Control and Dynamics，1996，19(3):702-703.

［4］程英容，张奕群.基于四元数反馈线性化的飞行器姿态控制方法研究［J］.航天控制，2007，25(5):13-16，27.Cheng Yingrong，Zhang Yiqun.Research on the quaternion feedback linearization for spacecraft attitude control［J］.Aerospace Control，2007，25(5):13-16，27.(in Chinese)

［5］Song C H，Kim S J，Kim S H，et al.Robust control of the missile attitude based on quaternion feedback ［J］.Control Engineering Practice，2006，14(7):811-818.

［6］管萍，陈家斌.挠性卫星的自适应模糊滑模控制［J］.航天控制，2004，22(4):62-67.Guan Ping，Chen Jiabin.The adaptive fuzzy sliding mode control for flexible satellite［J］.Aerospace Control，2004，22(4):62-67.(in Chinese)

［7］Banga H，Ha C K，Kim J H.Flexible spacecraft attitude maneuver by application of sliding mode control［J］.Acta Astronautica，2005，57(11):841-850.

［8］Hu Q L，Ma G F.Variable structure control and active vibration suppression of flexible spacecraft during attitude maneuver［J］.Aerospace Science and Technology，2005，9(4):307-317.

［9］唐超颖，沈春林.滑模变结构控制在航天器姿态控制系统中的应用［J］.兵工自动化，2004，23(1):1-3.Tang Chaoying，Sheng Chunlin.Application of variable-structure control with sliding mode in attitude control system of spacecraft［J］.Ordnance Industry Automation，2004，23(1):1-3.(in Chinese)

［10］孙兆伟，邬树楠，李晖.带有干扰观测器的凝视航天器姿态变结构控制［J］.哈尔滨工业大学学报，2010，42(9):1374-1377，1417.Sun Zhaowei，Wu Shunan，Li Hui.Variable structure attitude control of staring mode spacecraft with disturbance observer［J］.Journal of Harbin Institute of Technology，2010，42(9):1374-1377，1417.(in Chinese)

［11］Shtessel Y B，Shkolnikov A，Levant I A.Smooth second-order sliding modes:missile guidance application［J］.Automatica，2007，43(8):1470-1476.

［12］Levant I A.Higher-order sliding modes，differentiation and output-feedback control［J］.International Journal of Control，2002，76(9):924-942.