基于三维热弹性接触的汽轮机调节级叶片枞树型叶根轮缘结构的优化

张明辉，张 荻，谢永慧

（西安交通大学 能源与动力工程学院，西安710049）

随着经济的快速发展，电力需求持续增长，对发电机组的可靠性要求也不断提高.叶片作为汽轮机的重要零部件，主要功能是将热能转化为机械能，其安全可靠性直接影响机组的正常运行［1］.

调节级位于汽轮机通流部分之首，由于大负荷、高温及部分进汽等因素影响，在大功率汽轮机所有零部件中，调节级的工作条件是最苛刻的［2］.枞树型叶根具有装卸方便、叶根轮缘承载面接近等强度、承载能力高等优点，因而被广泛应用于大功率汽轮机调节级叶片上［3］.目前的枞树型叶根轮缘形状多是在常规状态下设计的，而调节级叶片工作在高温蒸汽中，由于叶片和转子的材料特性存在差异，线膨胀系数不同，随着温度的提高，叶根和轮缘存在很大的热变形，导致叶根轮缘接触不良，叶根齿的承载及应力状况发生很大的变化.因此，有必要在考虑高温热变形的影响下，对调节级枞树型叶根轮缘结构进行优化，提高叶片的安全性.

近年来，一些学者开展了通过改进叶根结构提高叶片性能的研究［4-14］，获得了一些成果.如西安交通大学涡轮机教研室［4］采用平面应力有限元分析程序对枞树型叶根轮缘应力进行了研究，得到了此类叶根轮缘合理结构设计的一些初步结论.李佳其等［5］、Papanikos等［7］和Meguid等［8］分别对叉型叶根、燕尾型叶根和枞树型叶根结构进行了分析，初步讨论了若干设计尺寸对叶根安全性的影响.2002年，Song等［9］以经济性为目标，对二维枞树型叶根进行多变量优化设计，获得了较好的优化效果.2005年，赵海［11］通过UG 软件对涡轮榫头／榫槽三齿结构进行了参数化建模，分析了主要设计参数及温度载荷对结构强度的影响.2009年，林香等［14］利用Ansys软件进行优化分析，降低了航空发动机燕尾型榫连接件的最大应力和接触应力.

国内外研究者在叶根轮缘的优化方面已经进行了一些研究，但大多集中于特定尺寸参数对目标函数的影响或对实际模型进行简化后的二维分析上，针对基于三维有限元分析的枞树型叶根轮缘结构优化，尤其是考虑高温影响下的优化研究仍然较少.近年来，随着加工工艺的提高及优化理论和优化算法的成熟，合理地设计叶根轮缘尺寸、提高叶片的强度性能变得切实可行且非常必要.

基于以上讨论，笔者利用Ansys软件建立了调节级枞树型叶根轮缘的参数化模型，在考虑高温影响下，以减小叶根轮缘处最大等效应力为目标，对叶根轮缘的关键尺寸进行了优化设计，最终获得了该叶根轮缘的优化型线.

1 热应力问题及结构优化方法

本文研究中考虑了高温热应力对汽轮机叶片的影响，并采用现代结构优化方法对调节级枞树型叶根轮缘结构进行了优化.

1.1 弹性热应力问题的有限元方程

物体温度发生变化时，由于热变形将产生线应变.如果物体各部分热变形不受任何约束，则物体发生变形而不产生应力.当存在约束或者温度变化不均匀，热变形不能自由进行时，物体中就会产生应力，即热应力［15］.当弹性体的温度场已知时，可以求解出弹性体各部分的热应力.

物体由于热膨胀只产生线应变，所以剪应变为零，这种由于热变形产生的应变可以看作是物体的初应变：

式中：α为材料的线膨胀系数；φ为结构的稳态或瞬态温度场；φ0为结构的初始温度场.

当物体中存在初应变时，应力与应变的关系可表示成

式中：D为弹性矩阵.

将式（2）代入虚位移原理的表达式，则可得到包括温度应变在内求解热应力问题的最小位能原理表达式，其泛函表达式如下：

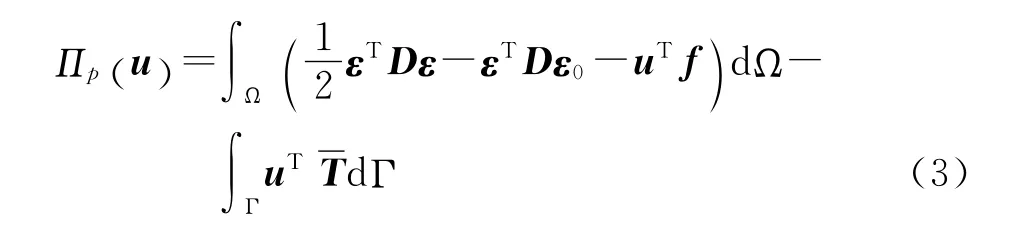
式中：Πp为结构总势能；u为结构位移；Ω 为体积域；Γ为表面域；f为体积力；T为表面力.

在求解域Ω 内进行有限元离散，得到有限元求解方程为：

式中：K为结构 刚度矩阵；a为节点位移向量；P为载荷.

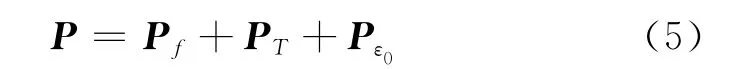
式中：Pf为体积载荷项；PT为表面载荷项；Pε0为温度应变引起的载荷项.

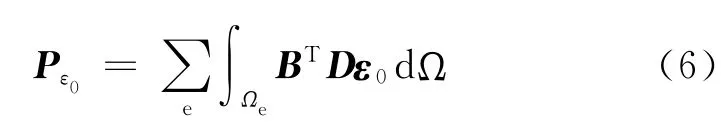
式中：B为应变矩阵.

由此可见，热应力问题与无热载荷的应力分析问题相比，除了增加一项以初应变形式出现的温度载荷Pε0外，其他完全相同.笔者充分考虑了汽轮机运行温度场对调节级叶片及轮缘的影响，建立了叶片与轮缘的三维热弹性接触有限元模型.

1.2 结构优化方法

现代结构优化理论由有限元计算和优化方法两部分组成［16］.目前为止，有限元分析方法已经广泛应用于航空航天、建筑和机械制造等领域，而优化方法也已形成了较完善的体系.

一般而言，基于参数化有限元分析的优化设计包括3个基本要素［17］（1）设计变量：设计过程中需要不断调整赋值的变量参数；（2）状态变量：设计过程需要满足的约束条件变量，是设计的因变量，设计变量的函数；（3）目标函数：设计中极小化的变量参数必须是设计变量的函数.

最优化问题的数学模型是找到一组设计变量x＝［x1，x2，…，xn］T，满足

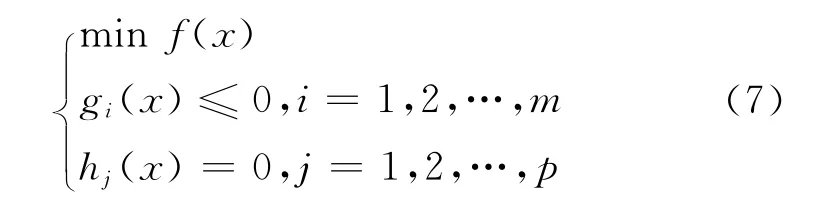
式中：x为设计变量，x＝［x1，x2，…，xn］T；f（x）为目标函数；gi（x）和hj（x）为约束条件或状态变量.

即在满足约束条件的前提下，找到一组最优的设计变量，使目标函数值达到最小.

结构优化的主要步骤包括建立数学模型和优化迭代控制［18］.建立数学模型即确立包括设计变量、约束条件和目标函数的分析模型；优化迭代主要是综合考虑优化效果和求解时间，选择一定的数学优化模型（即优化方法）.

笔者基于有限元分析软件Ansys建立调节级枞树型叶根轮缘的数学模型，采用模式搜索算法进行优化控制，完成结构优化工作.

模式搜索算法是一种直接优化方法，不依赖目标函数的导数信息求解最优化问题，在解决不可导函数或求导异常麻烦的函数的优化问题时非常有效［19］.本文使用的模式搜索算法由Ansys的参数化设计语言APDL编写，并通过对一个多峰函数求极值来验证其准确性.

对于函数

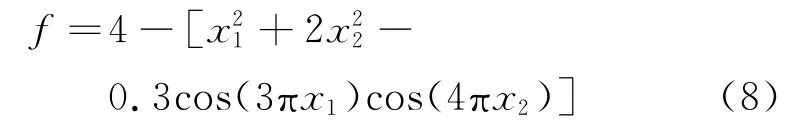
其中，-1.204≤x1≤1.204，-1.204≤x2≤1.204.理论解为：x1＝x2＝0时，f取得极大值4.3.

采用本文编写的算法，以x1和x2为设计变量，-1.204≤x1≤1.204，-1.204≤x2≤1.204为状态变量，-f为目标函数进行优化，获得的优化结果为x1＝3.815×10-7，x2＝2.289×10-7时，f取得极小值-4.300，所得结果与理论解非常吻合，从而验证了该算法的准确性.

2 计算模型

本文的研究对象是考虑高温影响并具有复杂接触状态的汽轮机调节级叶片叶根和轮缘.计算模型包括叶片和对应的转子部分，图1给出了计算模型的三维造型、整体网格及叶根轮缘接触处的网格.叶片和轮缘材料特性见表1.

图1 计算模型及网格Fig.1 The computational model and grid

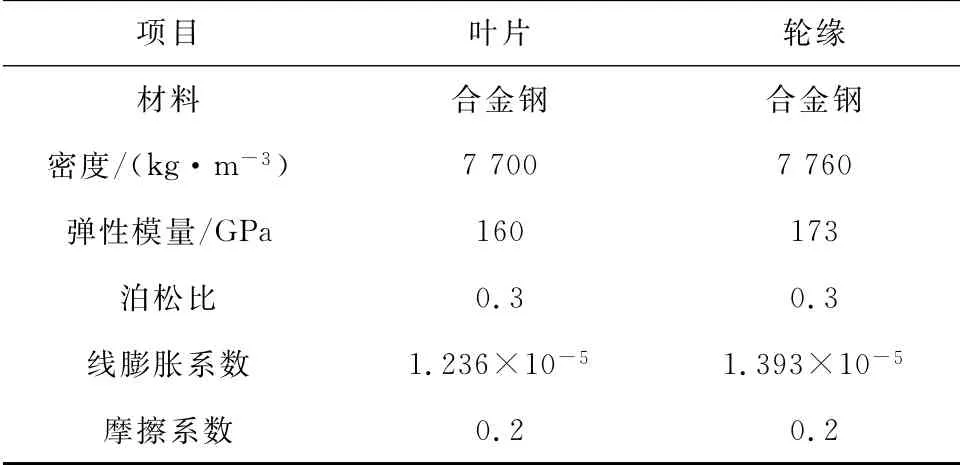
表1 叶片和轮缘材料特性Tab.1 Material properties of the blade and rim

有限元模型共有166 618单元、162 113节点.计算中对整个有限元模型设置了汽轮机工作转速3 000r／min的离心力.另外，根据相关研究［20-21］，汽轮机稳定运行时，调节级处沿轴心至转子外表面的径向温度梯度较小，尤其是转子顶部与叶根直接接触的轮缘部分的温度基本不变，为调节级的工作温度.因此，笔者依据相关透平制造企业经验，对计算模型设置调节级正常运行下的工作温度为534 ℃.计算模型的边界条件设置如下：（1）叶根轮缘承载设置接触边界面条件；（2）轮缘对称面节点设周期对称边界条件；（3）轮缘底部一列节点设径向约束；（4）轮缘底部中间节点设轴向约束.

3 结构优化过程及参数设置

3.1 结构优化过程

叶根轮缘结构优化是通过改变模型的某些关键尺寸参数完成的，在建立有限元模型的过程中，设计变量和约束变量必须以参数的形式出现［22］.因此，本文利用Ansys的参数化设计语言APDL 设置设计变量、状态变量（约束条件）和目标函数，完成叶根轮缘多参数计算模型的建立以及有限元计算的循环进行.

图2给出了叶根轮缘结构优化的流程图.

具体过程如下：

（1）为设计变量赋值，判断是否满足状态变量.如不满足，通过优化控制程序重新为设计变量赋值，如满足，则创建参数化模型.

（2）加载求解，进行有限元分析.

（3）由有限元分析结果中提取目标函数值，判断是否收敛.如果收敛，则退出优化循环，得出结果，否则通过优化控制程序重新为设计变量赋值并进行循环分析.

（4）得到最优方案后，对结果进行后处理.

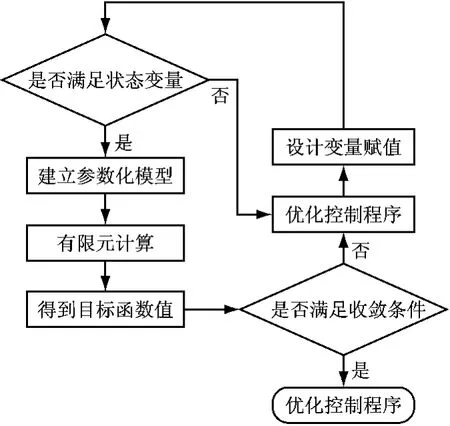
图2 优化过程流程图Fig.2 Flow chart of the optimization process

3.2 优化参数设置

（1）设计变量

综合考虑叶根轮缘各尺寸对应力分布的影响，选取8个关键尺寸作为设计变量进行研究，分别为叶根展开角度A、接触面倾角B、齿面间距Tp、齿面宽度Cl、叶根齿内圆角半径R1、叶根齿外圆角半径Rc1、轮槽外圆角半径R2和轮槽内圆角半径Rc2.图3为变量示意图.

（2）状态变量

为了保证优化过程中创建的模型在几何上合理，避免怪异的形状出现，模型尺寸必须满足一定的几何约束，即优化过程中的状态变量.如图3所示，对模型设置了5个状态变量：叶根轮缘非接触面的倾角C＞0；叶根齿面宽度Cl与轮缘承载面宽度Clr之差E的绝对值小于1，即-1＜E＝Cl-Clr＜1；叶根第三齿齿颈宽度L12＞4；叶根底部宽度L34＞1；轮缘底部宽度L56＞5.如果不满足以上几个条件，就会出现不合理的叶根轮缘结构，甚至导致叶根和轮缘实体部分的交叉以及网格划分时出错.因此，为了保证计算过程顺利进行，必须先对状态变量进行判定，在得到合理的几何结构之后，再进行建模和分析计算.

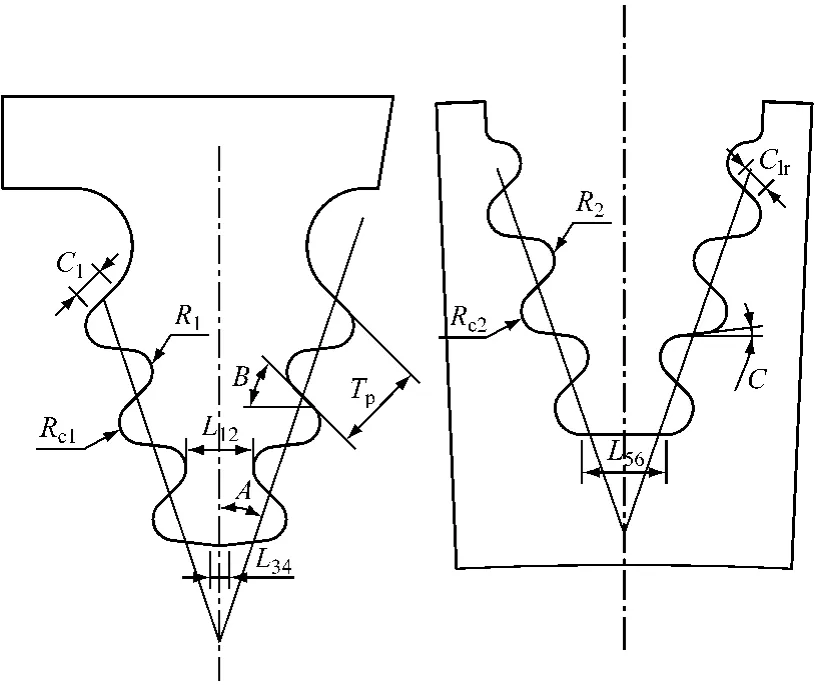
图3 变量示意图Fig.3 Schematic diagram of critical variables

（3）目标函数

以叶根和轮缘处最大等效应力的较大者Fmax作为目标函数.

经过最初几次试算，逐步排除不合理的叶根轮缘尺寸，得到了各变量较合适的取值区间，见表2.

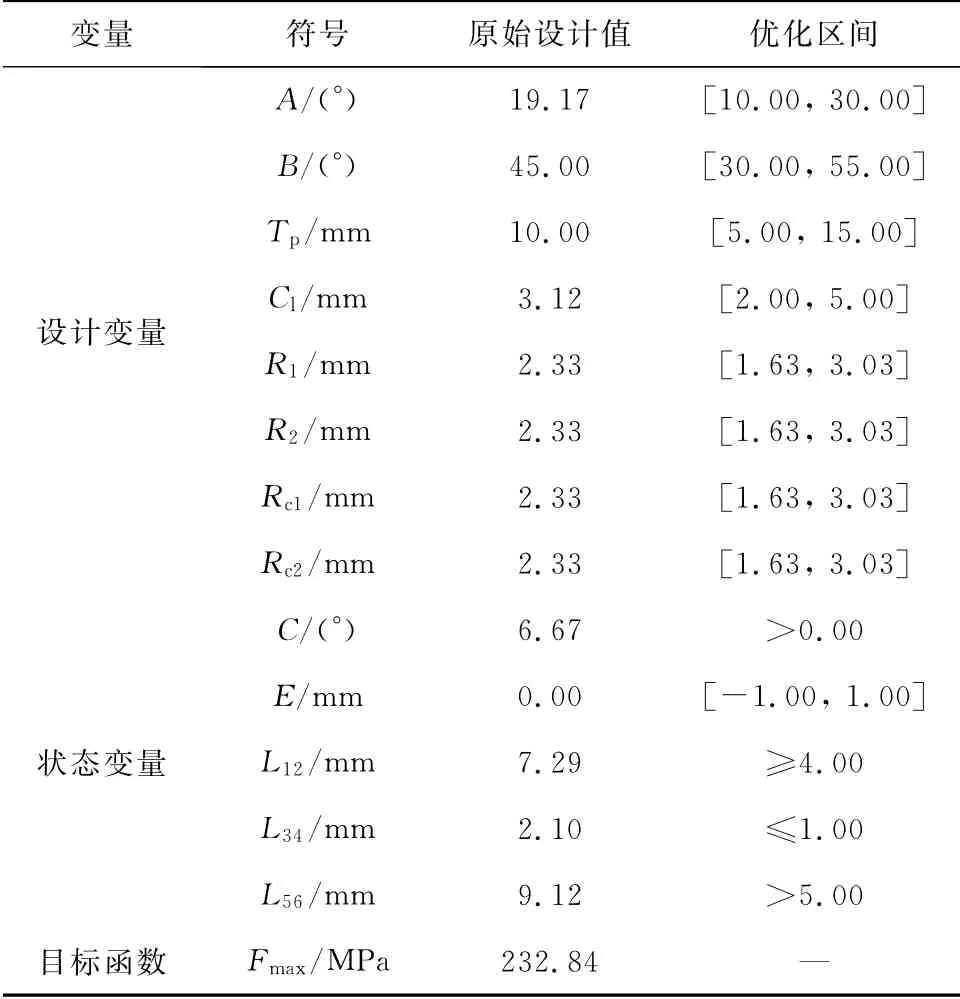
表2 变量的取值范围Tab.2 Range of variables

4 结果与讨论

4.1 原始叶根轮缘计算结果

首先对原始尺寸的叶根轮缘模型进行常温下（20 ℃）和高温下（工作温度534 ℃）的应力分析.图4和图5分别为叶片和轮缘在低温和高温下的等效应力云图.由图4和图5可见，常温下叶根处最大等效应力为154 MPa，轮缘处最大等效应力为169 MPa；高温下叶根处最大等效应力为233MPa，轮缘处最大等效应力为198 MPa.高温下叶根和轮缘的最大等效应力较常温下分别增大了51.3% 和17.2%，增幅较大.

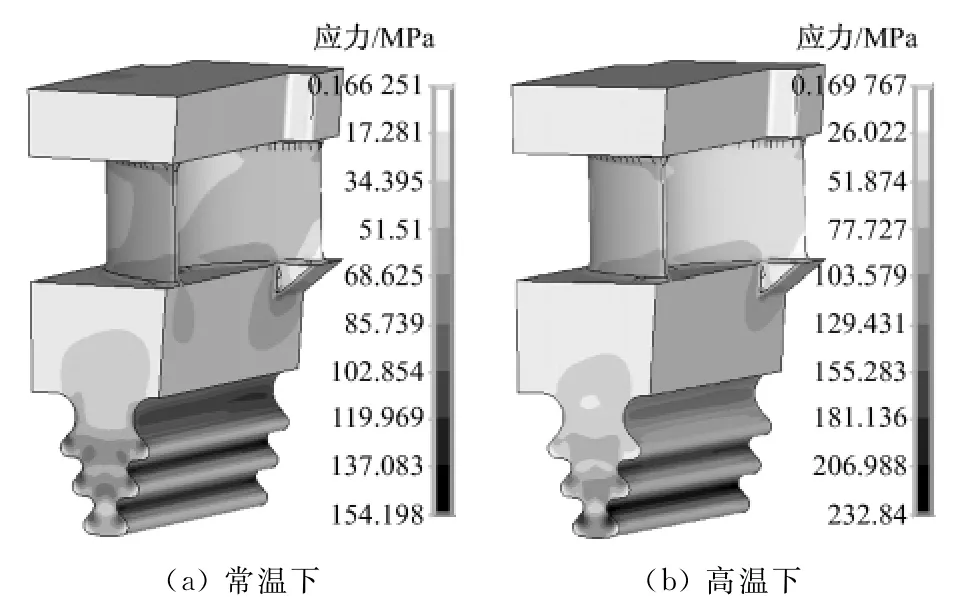
图4 叶片的等效应力图Fig.4 Equivalent stress contours of the blade

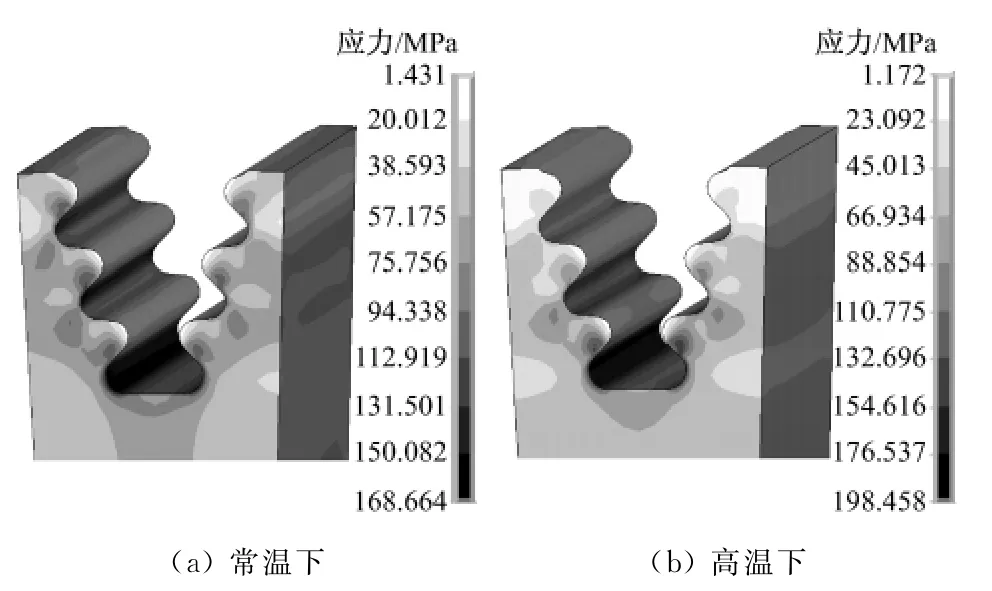
图5 轮缘的等效应力图Fig.5 Equivalent stress contours of the rim

另外，分别统计了常温和高温下叶根各齿面的承载状况，见表3.由表3可知，常温下压力面叶根齿和吸力面叶根齿的总承载在50%左右，两个面承载均匀，并且压力面和吸力面各齿的承载比例均在1／3左右，说明在常温下该枞树型叶根各齿接近等强度，设计合理；而在考虑了高温引起的热变形后，压力面和吸力面各齿的承载极为不均，第3齿的承载大大升高，而第1齿的承载则下降较多，如压力面第1齿承载变为10.05%，而第3齿承载变为55.91%，第3齿的承载已经超过了压力面总载荷的一半，并达到了第1 齿承载的5 倍以上，叶根的承载状况恶化.

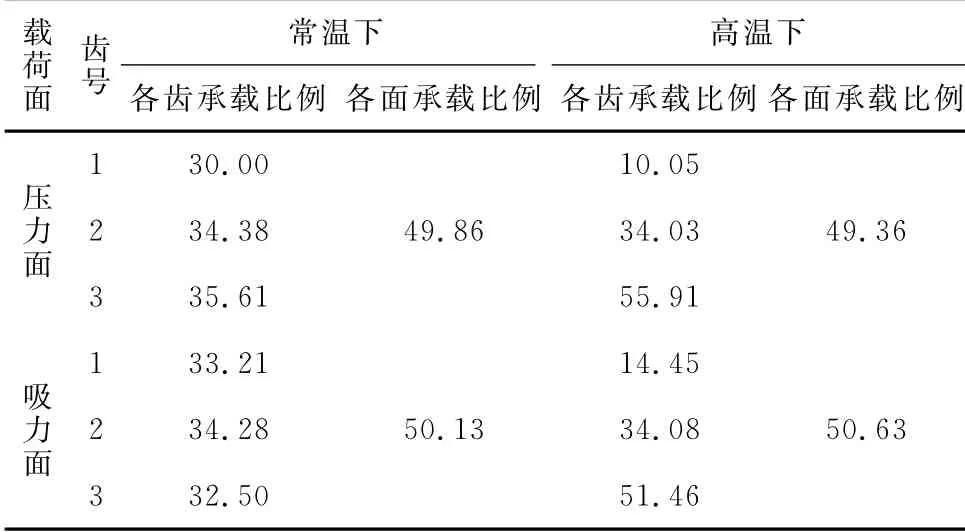
表3 叶根齿面承载分布Tab.3 Load distribution on root teeth %

由以上数据可以看出，对于调节级叶片，常温下设计良好的枞树型叶根轮缘，在高温下由于热变形的影响，叶根各齿的承载极为不均，导致产生大应力.叶根处的这种应力分布和承载状况为叶片的正常工作带来很大的安全隐患，因此有必要在考虑高温热变形影响的前提下对调节级枞树型叶根轮缘结构进行优化.

4.2 基于模式搜索算法的优化结果

4.2.1 优化过程

设置模式搜索算法的第一次迭代网格尺寸为1.当迭代次数超过100、网格尺寸小于1×10-4或目标函数残差小于1×10-4三者满足其一时，优化过程结束.

图6～图8显示了模式搜索的具体过程.图6给出了每次迭代得到的最佳函数值.由图6可以看出，经过大约4次成功搜索后，目标函数值已经接近最佳值.从第15步开始，函数值开始趋于平稳，逐步逼近最优值185.58MPa.图7为每次迭代的网格尺寸.每次成功的迭代后网格尺寸增加，失败的迭代后网格尺寸减小，本次计算最终的网格尺寸为6.1×10-5，满足收敛条件，优化结束.图8给出了每次迭代对应的计算次数，本次分析共计算了306次.可以看到，当目标函数趋近于最优值时，由于网格尺寸越来越精细，需要多次调整才能找到合适的网格尺寸，所以每次迭代的计算次数增加.

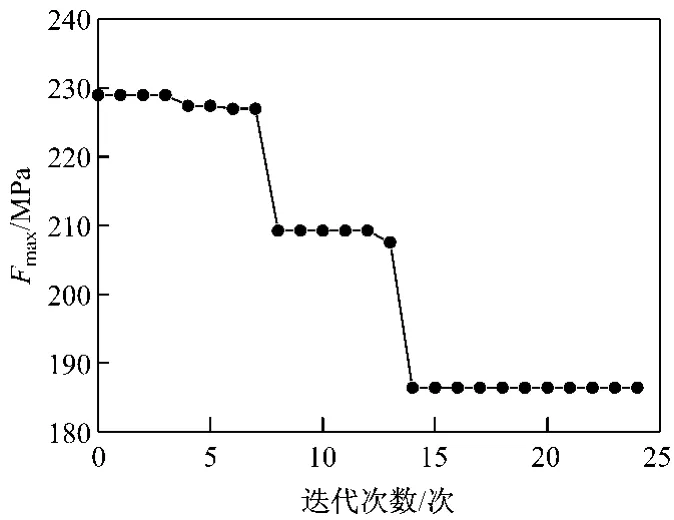
图6 目标函数变化曲线Fig.6 Variation curve of objective function

4.2.2 结果分析

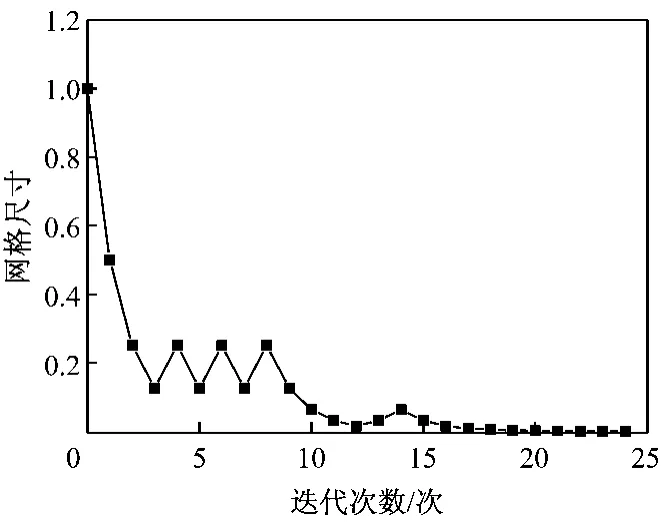
图7 网格尺寸变化曲线Fig.7 Variation curve of mesh size

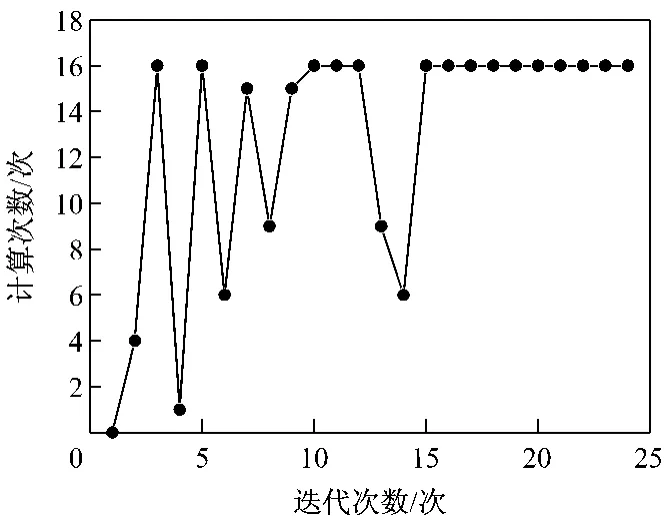
图8 每次迭代计算次数变化曲线Fig.8 Calculation counts in each iteration

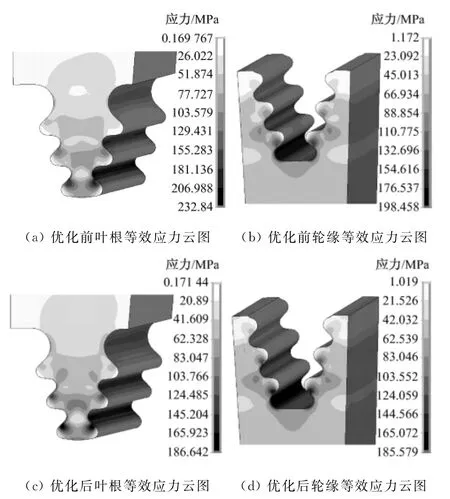
图9 优化前后叶根和轮缘等效应力图Fig.9 Equivalent stress of root and rim before and after optimization

图9给出了优化前后叶根轮缘的等效应力云图.对比图9（a）和图9（b）可以看到，优化前后叶根轮缘的应力分布大体相同，但最大等效应力值有较大变化.优化前，叶根最大等效应力为232.84MPa，位于压力面第三齿圆角处，优化后，叶根最大等效应力为186.64 MPa，同样位于压力面第三齿圆角处，但比优化前降低了19.84%，优化效果明显；轮缘处最大等效应力在优化前为198.46 MPa，优化后为185.58 MPa，均位于压力面第三齿圆角处，优化后比优化前降低了6.48%，优化效果也较好.同时，优化后叶根和轮缘处的最大等效应力相近，承载状态改善，有利于叶片安全工作.

此外，为了解叶根型线上应力的整体变化趋势，给出了优化前后叶根中截面曲线a-b（图10）上的等效应力分布（图11）.同时，考虑到叶根最大应力常出现在压力面第三齿圆角处，给出了优化前后叶根压力面第三齿圆角处曲线c-d（图10）上的等效应力分布（图12）.在图11中，按由a至b的路径，曲线中共出现5处峰值，除中间小峰值为叶根底部的应力外，其余四处依次表示吸力面第二齿圆角、吸力面第三齿圆角、压力面第三齿圆角、压力面第二齿圆角处的应力值.从图11可以看出，优化前后沿叶根型线的应力分布总体趋势不变，在叶根齿圆角处应力值较大，第三齿圆角处应力较第二齿圆角处大.优化前，压力面第三齿圆角处应力明显高于其他部位；优化后，压力面第三齿圆角处应力大幅减小，第二齿圆角处应力也有一定程度减小，吸力面第二齿和第三齿圆角处应力变化较小，另外各齿圆角处的应力差别减小，趋于均匀化，满足枞树型叶根等强度设计的要求.从图12c-d曲线的应力分布可以看出，优化后压力面第三齿圆角处整体应力水平明显降低.

图10 曲线a-b 和曲线c-d 位置示意图Fig.10 Diagram of curves a-b and c-d

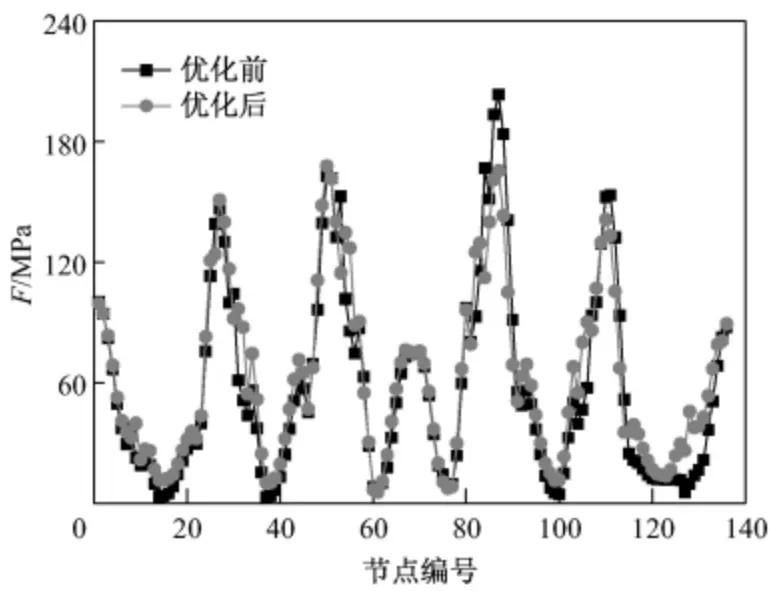
图11 优化前后a-b 曲线上等效应力分布Fig.11 Equivalent stress distribution along curve a-b before and after optimization

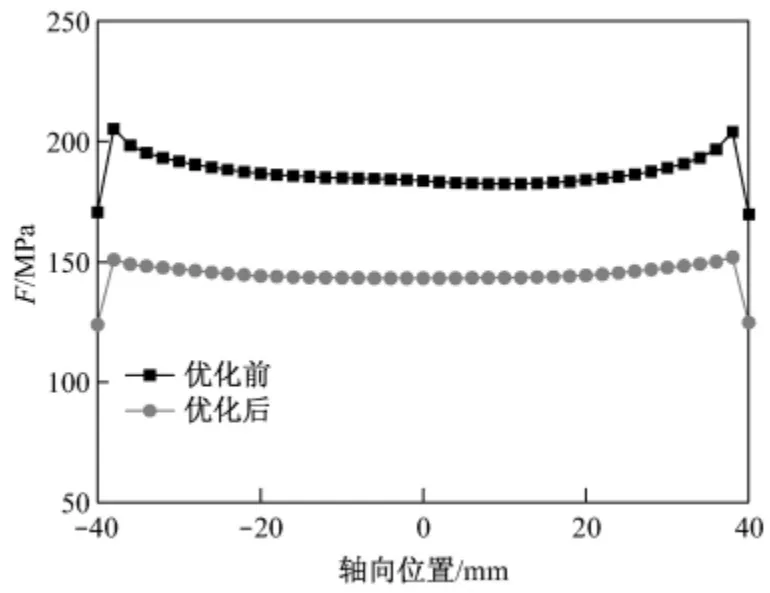
图12 优化前后c-d 曲线上等效应力分布Fig.12 Equivalent stress distribution along curve c-d before and after optimization

整体看来，经过优化，叶根轮缘处的应力水平大幅降低，承载状况得到改善，优化效果明显.

表4给出了优化前后设计变量的数值.

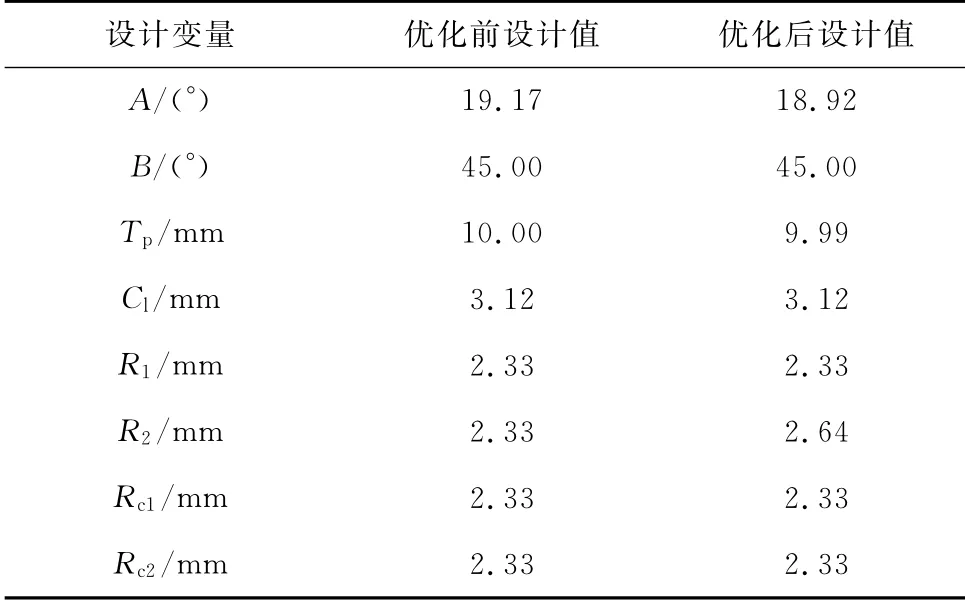
表4 优化前后设计变量数值Tab.4 Values of design variables before and after optimization

5 结 论

（1）通过有限元分析软件Ansys的参数化语言APDL，建立调节级枞树型叶根轮缘结构的参数化分析模型，使用优化算法控制优化过程，进行叶根轮缘的结构优化，能获得相关尺寸的最优值，大大降低叶根轮缘的应力水平.此套方法可行且有效，具有良好的工程实用价值.

（2）对于调节级叶片，常温下设计良好的枞树型叶根轮缘由于在高温下受热变形的影响，其应力分布和齿面承载状况变得恶劣，存在安全隐患.

（3）对于本文的调节级枞树型叶根轮缘模型，选取8个特征尺寸作为设计变量、叶根轮缘处最大等效应力为目标函数，采用模式搜索算法进行优化控制，对调节级枞树型叶根轮缘结构进行优化分析，获得了叶根轮缘的优化型线.优化后，叶根最大等效应力下降了19.84%，轮缘最大等效应力下降了6.48%，叶根各齿圆角处应力趋于平稳.整体优化效果良好，提高了叶片运行的可靠性.

［1］王立清，盖秉政.含表面裂纹T 型叶根应力强度因子的数值 计 算［J］.动 力 工 程，2008，28（2）：169-171，220. WANG Liqing，GAI Bingzheng.Numerical calculation of stress intensity factors for blade’s T-root part with a surface crack ［J］.Journal of Power Engineering，2008，28（2）：169-171，220.

［2］范小平，周振杰，李曦滨.新型135MW 汽轮机调节级叶片开发设计［J］.东方电气评论，2010（1）：33-35. FAN Xiaoping，ZHOU Zhenjie，LI Xibin.Design of new governing stage blade for 135 MW steam turbine［J］.Dongfang Electric Review，2010（1）：33-35.

［3］吴厚钰.透平零件结构和强度计算［M］.西安：西安交通大学出版社，2007.

［4］涡轮机教研室.用有限元方法讨论枞树形叶根的合理结构［J］.西安交通大学学报，1977，11（2）：59-74. Turbine Teaching and Research Section.Research on the proper structural of a turbine blade with fir-tree root by finite element method［J］.Journal of Xi’an Jiaotong University，1977，11（2）：59-74.

［5］李家其，贾立言，徐光辉，等.叉型叶根的改进设计研究［J］.汽轮机技术，1992，34（4）：20-23. LI Jiaqi，JIA Liyan，XU Guanghui，etal.Research on improvement design of fork-shaped blade root［J］.Turbine Technology，1992，34（4）：20-23.

［6］邢誉峰，诸德超.航空发动机涡轮盘榫槽的形状优化设计［J］.航空学报，1995，16（4）：488-491. XING Yufeng，ZHU Dechao.Shape optimum design of engine’s turbodisk tenon-grooves［J］.Acta Aeronautica et Astronautica Sinica，1995，16（4）：488-491.

［7］PAPANIKOS P，MEGUID S A，STJEPANOVIC Z.Three-dimensional nonlinear finite element analysis of dovetail joints in aeroengine discs［J］.Finite Element in Analysis and Design，1998，29（3／4）：173-186.

［8］MEGUID S A，KANTH P S，CZEKANSKI A.Finite element analysis of fir-tree region in turbine discs［J］.Finite Elem and Design，2000，35（4）：305-317.

［9］SONG W B，KEANE A，REES J，etal.Turbine blade fir-tree root design optimization using intelligent CAD and finite element analysis［J］.Computer and Structures，2002，80（24）：1853-1867.

［10］马全海.面向对象的随机有限元与接触问题的可靠性形状优化设计研究［D］.南京：南京航空航天大学能源与动力学院，2002.

［11］赵海.涡轮榫头榫槽结构设计方法研究［D］.南京：南京航空航天大学能源与动力学院，2005.

［12］姚利兵，莫蓉，刘红军，等.基于强度约束的叶片榫头参数化设计［J］.航空制造技术，2007（8）：93-95. YAO Libing，MO Rong，LIU Hongjun，etal.Strength constraint based parameterized design of turbine blade serration［J］.Aeronautical Manufacturing Technology，2007（8）：93-95.

［13］杨敏超，孙苏亚.涡轮榫头榫槽的结构优化设计［J］.航空动力学报，2010，25（8）：1876-1882. YANG Minchao，SUN Suya.Structural optimization of turbine tenon／mortise［J］.Journal of Aerospace Power，2010，25（8）：1876-1882.

［14］林香，黄致建，郝艳华.燕尾型榫连接件的结构优化设计［J］.制造业信息化，2009（10）：61-63. LIN Xiang，HUANG Zhijian，HAO Yanhua.The optimization design of the dovetail tenon joints［J］.Mechanical Engineer，2009（10）：61-63.

［15］王勖成.有限单元法［M］.北京：清华大学出版社，2003.

［16］陈卫东，蔡萌林，于诗源.工程优化方法［M］.哈尔滨：哈尔滨工程大学出版社，2006.

［17］博弈创作室.APDL参数化有限元分析技术及其应用实例［M］.北京：中国水利水电出版社，2005.

［18］梁醒培，王辉.基于有限元方法的结构优化设计［D］.北京：清华大学出版社，2010.

［19］吴兴远.模式搜索法在最优化问题中的应用［J］.软件导刊，2009，8（8）：122-123. WU Xingyuan.Application of pattern search in optimization problem［J］.Software Guide，2009，8（8）：122-123.

［20］郑李鹏.基于APDL 的联合循环汽轮机转子热应力计算及启动优化的研究［D］.浙江：浙江大学能源工程学院，2011.

［21］马环宇，杨敏强，李勇.300 MW 汽轮机调节级的温度场分析［J］.东北电力大学学报，2007，27（2）：14-17. MA Huanyu，YANG Minqiang，LI Yong.Temperature distribution analysis of governing stage for 300 MW steam turbine［J］.Journal of Northeast Dianli University，2007，27（2）：14-17.

［22］许素强，夏人伟.结构优化方法研究综述［J］.航空学报，1995，16（4）：385-393. XU Suqiang，XIA Renwei.Methods of structural optimization：an overview［J］.Acta Aeronautica et Astronautica Sinica，1995，16（4）：385-393.