灰色聚类法在林区路面性能综合评价中的应用1)

任重昕 刘 双

(东北林业大学，哈尔滨，150040)

灰色聚类是根据灰色关联矩阵或灰数的白化权函数，将一些观测指标或观测对象划分为若干个可定义类别的方法，一个聚类可以看成是属于同一类的观测对象的集合。按聚类对象划分，灰色聚类可分为灰色关联聚类和灰色白化权函数聚类［1］。

我国林区分布广泛，各地林区道路路面使用性能在不同地区、不同路段、不同的自然环境下对其影响程度不同，因此我国推广实施的路面使用性能评价模型权重值并不一定适合所有地区的所有路面。同时，在实际的使用中，路面使用性能评价结果与养护决策之间的联系不紧密，对路面各项评价指标之间的关系研究不够，以经验评价为主的现象仍然存在，权重的取值存在较大的主观性，导致在综合评价方面缺乏定量计算的决策依据。因此，有必要根据各地的实测数据，建立一个客观的路面使用性能评价模型，为林区路面养护决策提供理论依据。以黑龙江省林区道路为依托，本文采用灰色白化权函数聚类对路面的使用性能进行建模分析和评价。

1 评价模型的引入

研究灰色系统，关键是使其在一定条件下白化，从而运用数学理论对其分析研究［2］。白化权函数就是用来描述一个灰数对其取值范围内不同数值的“偏爱”程度，是使灰色系统向白色系统转化的过程。一般来说，一个灰数的白化权函数是研究人员根据已知信息设计的，没有固定的程式，函数曲线的起点和终点应有其含义。

1.1 基于中心点三角白化权函数的灰色评估方法

第一步:设有n个对象，m个评估指标，s个不同的灰类，对象i关于指标j的样本观测值为xij，i=1、2、…、m。按照评估要求所需划分的灰类数s，选取 λ1、λ2、…、λs为最属于灰类1、2、…、s的点(以属于灰类最大可能性的点为选取依据，称为中心点，在此选取中点)，将各个指标的取值范围也相应的划分为s个灰类，例如将j指标的取值范围［λ1，λs+1］划分为s个小区间:［λ1，λ2］、［λ2，λ3］、…、［λk－1，λk］、…、［λs－1，λs］;其中 λ1＜λ2＜λ3＜…＜λs－1＜λs。

第二步:同时连接点(λk，1)与第k－1个小区间的中心点(λk－1，0)以及与第k+1个小区间的中心点(λk+1，0)，得到j指标关于k灰类的三角白化权函数对于，可分别将j指标的取值域向左、右延拓至λ0、λs+1，可得j指标关于灰类1的三角白化权函数

对于指标j的一个观测值x，由式(1)计算其属于灰类k(k=1、2、…、s)的隶属度

第三步:按式(2)计算对象i(i=1、2、…、n)关于灰类k(k=1、2、…、s)的综合聚类系数。

第四步:根据判断对象i属于灰类k*，当有多个对象同属于k*灰类时，还可以进一步根据综合聚类系数的大小确定同属于k*灰类的各个对象的优劣或位次。

1.2 基于熵值法的权重确定方法

设有m个方案，n个决策指标，指标值为xij(1≤i≤m，1≤j≤n)，计算步骤如下［3］:

第一步:按式(3)将决策矩阵X=xij用线性比例变换法作标准化处理，得到标准化矩阵。

再对求得的标准化矩阵Y进行归一化处理，如式(4)所示。

第二步:按式(5)计算第j个指标的熵值。

式中:k＞0，ej≥0;对于指标j，如果pij全都相等，即pij=1/m(i=1、2、…、m)，那么ej取极大值，即ej=klnm，这里取k=(lnm)－1。

第三步:计算第j个指标的偏差程度系数。

根据第j个指标的熵值ej的大小与该指标各方案属性值的偏差程度相反的原则，定义指标j下的各方案属性值的偏差程度系数，如式(6)所示。

第四步:计算各指标的权重 ωj和调整，如式(7)所示。要对计算出的各指标的权重进行修正调整，但必须保证

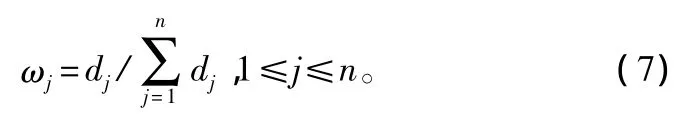
2 研究对象的确定

对于建立林区道路路面使用性能评价模型，有以下三点基本要求［4］:①选取的各项评价指标要有代表性和可比性，能满足路面性能特点的实际情况;②评价过程中尽量减少人为主观因素的影响;③整个综合评价模型应有较好的客观性、有效性、可操作性和经济可行性。

现行规范如JTGH20—2007《公路技术状况评定标准》，路面综合评价使用路面使用性能指数PQI，按式(8)计算［5］。

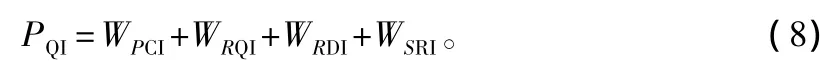
式中:WPCI、WRQI、WRDI和WSRI分别表示路面损坏指数PCI、路面平整度指数RQI、路面车辙指数RDI和抗滑性能指数SRI在PQI中的权重。虽然该方法能方便地实现路况的评价，但是线性加权的综合方式不理想，不能全面地反映出问题。

2008年对林区道路路况的调查结果显示:绝大部分路段的PCI在85～95之间，路面损坏等级基本介于优和良，优良级的比例占全部里程的99%，路面损坏状况较好;大部分路段的RQI值范围为60～91，路面平整度状况处于优良级的比例为63.3%;路面抗滑性能主要为优良级;路面结构强度符合要求;路面车辙状况处于优级和良级的比例占全部里程的84.1%。根据上述路况检测数据，本文选取其中5个路段并采用本文确定的方法对其路面使用性能进行分析，具体数据如表1所示。

表1 路面使用性能检测数据

3 林区道路路面使用性能综合评价

3.1 各指标中心点三角白化权函数计算

以路面行驶质量PCI指标为例，确定中心点三角白化权函数。由于JTGH20—2007《公路技术状况评定标准》中对路面使用性能的各项评价指标的分级标准相同，因此PQI、PDI和SRI的白化权函数也相同。PCI指标分为优、良、中、次、差5个等级。属于灰类最大可能性的点(95、85、75、65、55)将PCI的取值范围相应的划分为5个灰类，并分别将PCI指标的取值域向左、右延拓称为更优和更差类。以0、1、2、3、4、5、6 分别代表更优、优、良、中、次、差、更差，则PCI指标的中心点三角白化权函数划分如图1所示。

根据式(1)，PCI指标的中心点三角白化权函数如下所示:

图1 PCI指标的中心点三角白化权函数示意图

3.2 各路段对各指标的隶属度计算结果

根据3.1中各项评价指标的中心点三角白化权函数，计算各路段对各指标的隶属度(见表2～表6)。

表2 路段1的隶属度

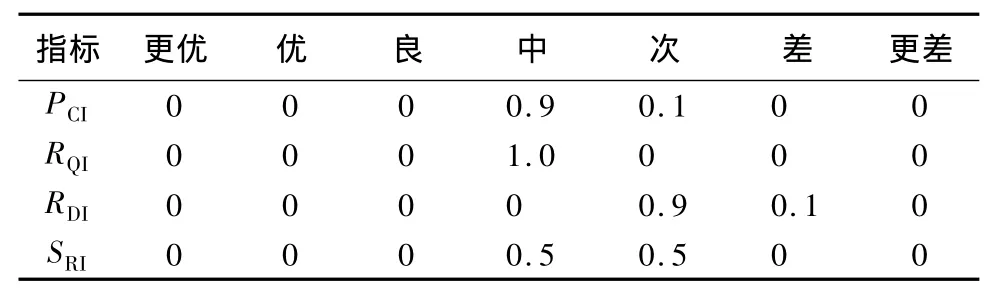
表3 路段2的隶属度

表4 路段3的隶属度

表5 路段4的隶属度

表6 路段5的隶属度

3.3 各指标权重的确定

路况数据规范化处理:根据式(3)和式(4)，对原路况数据矩阵用线性比例变换得到标准化矩阵yij和规范化矩阵pij，分别为:

计算各指标的熵值:根据式(5)计算各指标的熵值，此时，k=(ln5)－1。e1=0.996、e2=0.990、e3=0.994、e4=0.997。

计算各指标的偏差程度:根据式(6)计算各指标的偏差程度，d1=0.004、d2=0.010、d3=0.006、d4=0.003。

计算各指标的权重:根据式(7)计算各指标的权重值，ω1=0.17、ω2=0.44、ω3=0.26、ω4=0.13。

对各组合权重进行较正:根据路段原始数据，相比PCI指标值，RDI指标值较低、分布不均、范围广，应是评价的重点。因此，在建议范围之内，PCI取最小值0.30，调整后的 4 项评价指标权重为 0.30、0.44、0.13、0.13。

3.4 计算各路段关于各灰类指标的综合聚类系数

根据式(2)和熵值法的计算结果，得到各路段关于各灰类指标的综合聚类系数σ(见表7)。

表7 各路段综合聚类系数表

3.5 对各路段的使用性能进行灰色评价

对表7结果进行分析，把更优和优，差和更差的概率，分别合并为优和差，若聚类系数，则判断对象i属于灰类k*。据此，可判断出各路段的所属等级，并与JTGH20—2007《公路技术状况评定标准》中的综合评价模型得到的结果对比分析(见表8)。

表8 各路段评价结果及对比

对比分析路况检测数据表1和路段评价结果表8，规范评估路段4的路面综合使用性能指数PQI值为71.65，靠近中和次级的分界点，对其等级的划分不好判定。按照规范绝对分级标准评定等级为中，而采用基于概率的灰色评估，其状态为次，更具有客观合理性。规范评价路段3的PQI值为71.00，等级为中;而灰色评价其隶属于优、良、中、次、差的概率分别为0.103、0.327、0.091、0.039、0.440，判断其属于中等级的概率最小，而属于差等级的概率最大，因此，判断路段3的等级为差类。对比参照路段3的路况数据，其RQI值为52，属于差等级，已严重影响了行车安全性和舒适性，由此确定的养护类型为中修罩面。

4 结论与讨论

通过比较发现，采用灰色聚类法对林区道路5个路段进行评价，评价结果与实际情况更加吻合，结果更加客观。因此，运用灰色聚类法对路面使用性能进行评价，能够比较客观地反映路面的实际状况和各指标之间的相互影响，其结果和规范具有比较好的一致性。

本文利用灰色聚类法对路面使用性能进行综合评价，建立了灰色评价模型，并与规范进行了对比。该方法有效地克服了传统评价方法各指标权重取值人为因素影响较大的缺点。计算结果表明:该模型具有较好的适用性，评价分析结果对科学预测林区路面使用性能以及养护维修措施提供了可靠的依据。

［1］杜朝伟，朱罡.基于灰色聚类法的高速公路沥青路面使用性能综合评价［J］.中外公路，2007，27(5):67－70.

［2］刘思峰，谢乃明.灰色系统理论及其应用［M］.北京:科学出版社，2008.

［3］唐文彬，韩之俊.基于熵值法的财务综合评价方法［J］.南京理工大学学报，2001，25(6):650－653.

［4］王宁宁，刘燕.模糊综合评价法在高速公路路面使用性能评价中的应用［J］.公路交通技术，2007(9):123－127.

［5］交通部.JTG H20—2007公路技术状况评定标准［S］.北京:人民交通出版社，2007.