长白山主要树种直径生长的多元回归预测模型:以云杉为例1)
刘 洋 亢新刚 郭艳荣 高北延 冯启祥
(省部共建森林培育与保护教育部重点实验室(北京林业大学),北京,100083)(北京林业大学) (吉林省汪清林业局)
林分内各种大小直径的树木的分配状态,直接影响树木的树高、干形、材积、材种及树冠等因子的变化;林木直径可以被快速、方便且准确地测量,同时它是许多森林经营技术及测树制表技术理论的依据[1]。因此,直径生长模型一直是单木模型的研究重点,它是一个或一组数学函数式,描述林木生长及林分状态与立地条件、林分密度、周围相邻木距离、环境因子等变量之间的关系,并经一定方法处理后可预估林分直径生长量、收获量和林木枯损量。
直径回归方程是建立林分生长与收获模型的基础。国内外有关直径预测模型也很多,大多数都是以经验和理论生长方程为基础拟合[2-7],只考虑了林分密度,没有考虑立地质量和对象木与相邻木的最近距离对林木直径生长的影响,多数都涉及的是与距离无关的林分的单木模型。笔者利用3个竞争指数反映立地质量、林分密度和对象木与相邻木的最近距离,对直径潜在生长函数进行修正,从而合理预测林木的未来直径大小,为林分直径生长模型提供一种新的途径。
1 研究区概况
研究区位于吉林省汪清林业局金沟岭林场,地理位置 130°10'E,43°22'N。地貌属低山丘陵,海拔为300~1 200 m,坡度多在5°~25°。该区属季风型气候,全年平均气温3.9℃左右,积温2 144℃,年降水量600~700 mm,生长期为120 d。土壤多为针叶林灰棕壤,沟谷是草甸土、泥炭土、沼泽土或冲积土,结构一般为黏壤土类,粒状结构,湿松,根系多,平均厚度在40 cm左右。研究区为天然针阔叶混交过伐林。主要树种有:云杉(Picea koraiensis)、冷杉(Abies nephrolepis)、红松(Pinus koraiensis)、枫桦(Betula costata)、椴树(Tilia amurensis)等,其它树种还有:色木槭(Acer mono)、水曲柳(Fraxinus mandschurica)、胡桃楸(Juglans mandshurica)、黄菠萝(Phellodendro namurense)、白桦(Betula platyphylla)、青楷槭(Acertegmentosum)、花楷槭(Acer ukurunduense)等。
2 材料和方法
2.1 数据资料
数据来源于1982—1988年在吉林省汪清林业局金沟岭林场设立的26块皆伐标准地的1381株云杉解析木和101株云杉标准木,26块皆伐标准地林型基本一致,土壤类型均为棕色森林土。在数据分析时主要查阅了以下外业调查表。
土壤调查表:包括土壤种类、湿度以及土壤表面的枯落物厚度、腐殖质层厚度和土壤总厚度;
环境因子调查表:包括标准地位置的海拔高度、地形、坡位、坡度和坡向等因子;
每木调查表:记载了林分状况及对象木与邻近树木的位置关系、胸径、树高、枝下高和冠幅。
在标准地外业调查表的基础上,计算出皆伐标准地树种组成、林分密度、断面积、蓄积量等因子,具体情况见表1。

表1 长白山地区26块皆伐标准地基本概况
2.2 研究方法
选用潜在生长量修正法建立林木直径生长模型。模型用数式可表示为:

式中:D为林木直径;MD为修正函数;y为潜在直径生长函数。
由于林木间相互竞争,林分内绝大多数林木实际生长量小于潜在生长量,减小的程度与竞争程度有关[1]。从理论上来说,林木潜在生长函数应由疏开木的生长过程来确定。由于疏开木难以确定,有些研究者建议用相同年龄时优势木的生长过程代替疏开木的生长过程[8]。本研究在生长模型建模中,假定环境条件一致的条件下,选取18块皆伐标准地林分内的优势木直径,确定林木直径的潜在生长量,以Richards方程建立了潜在直径生长函数。然后用反映立地质量、林分密度、林木最近距离的3个竞争指数即地位级曲线方程、树冠竞争因子和2参数的Weibull分布函数所表示的修正函数对直径潜在生长函数进行修正。采用SPSS软件对参数进行拟合,并依据相关系数最大,剩余平方和最小得到直径实际生长的多元回归预测模型。
3 结果与分析
3.1 潜在直径生长函数的建立
树木生长理论方程有Logistic方程、Mitscherlich方程、Richards方程,理论上可以证明Logistic方程和Mitscherlich方程均是Richards方程的特例,并且Richards方程是近代应用最为广泛、适用性较强的一类生长曲线方程。因此,笔者以Richards方程为基础,研建直径的潜在生长量函数。Richards方程的形式为:

式中:y为优势木的直径;A为优势木年龄;M、K、B为方程参数。
Richards方程中各参数的生物学意义:参数M为y的最终值即上渐近值,即给出生长因子最终达到值;参数B决定曲线形状和拐点位置;参数K起着调节生长时间的作用,此值越大,生长时间便越短,它与生长速率是密切相关的[9]。
依据18块皆伐标准地林分内的优势木直径和年龄,利用SPSS软件对上述公式(2)进行拟合,得到M=55.253,K=0.018,B=2.389,R2=0.871。疏开木直径潜在生长函数为:
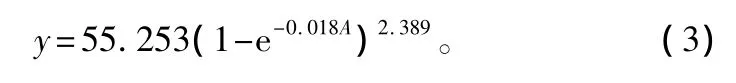
3.2 地位级
林木胸径的大小与立地质量有关。此外由于林分高也比较容易测定,与平均胸径及蓄积量相比,受林分密度影响较小,所以地位级作为评价立地质量高低的依据为各国普遍采用。常用的拟合地位级的数学模型有:对数双曲线式、对数曲线式、抛物线式、单分子式、理查兹式和双曲线式等。
本研究选取研究区78株云杉标准木的树高和年龄,采用SPSS软件对地位级的上述6个数学模型进行拟合。6个曲线方程中,对数曲线式lg(H)=a+blg(A)的相关系数(R2=0.895)最大,且参数a=0.350,b=0.448。因此,地位级曲线方程为:

式中:H为林分平均高;A为林分年龄;a、b为待定参数。
3.3 林分密度
林分密度说明林木对其所有空间的利用程度,它是影响林分生长和木材数量、质量的重要因子。林分中林木间的拥挤程度取决于林分密度、林木平均大小以及林木在林地上的分布。自由树的树冠冠幅与树木胸径之间呈显著的线性正相关,这种线性关系不随树木的年龄及立地条件的变化而改变,这正是利用树冠反映林分密度的可靠依据。Krajicek等[10]利用这一关系提出了树冠竞争因子(FCC)。(FCC)的具体确定方法如下:
①以疏开木的冠幅与胸径间的相关关系为基础,求出最大树冠面积。设疏开木冠幅与胸径的关系为:

式中:Cw为优势木冠幅;D为优势木胸径;a、b为待定参数。
依据18块皆伐标准地林分内的优势木胸径与冠幅,利用上述公式(5)进行拟合。拟合结果为:a=5.906,b=0.240,R2=0.884。即:

②对于胸径为Di的林木最大树冠面积应等于同胸径的疏开木树冠面积(AMC)i,即:
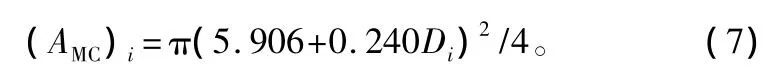
③将单位面积林分中每株树木的最大树冠面积相加即为该林分的树冠竞争因子(FCC)。即:

式中:Di为自由树(林分中优势木)胸径;N为林分密度,由表1中查得。
3.4 林木最近距离的影响
林木的生长不仅取决于其自身的生长潜力,而且还取决于其与周围竞争木的竞争能力。竞争能力的大小决定于竞争木与对象木之间的距离。根据文献[11],林木最近距离分布为单峰型,可用Weibull分布函数予以恰当描述。对于林木水平分布格局为团状或随机分布的森林群落(如结构丰富的天然林)而言,其林木最近距离分布仅用 2参数的Weibull分布函数(a=0)足以很好地表达;而对于林木水平分布格局为十分均匀的森林群落(如人工林)而言,其林木最近距离分布才需要用3参数的Weibull分布来描述。
本研究对象为天然林a=0,则2参数Weibull分布函数为:
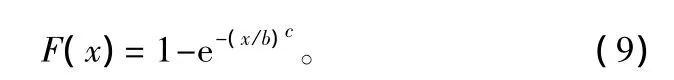
式中:b为尺度参数;c为形状参数;x为解析木与其周围相邻木的最短距离,其取值为0.5,1,1.5,2,…4。
通过SPSS软件,以长白山地区18块皆伐标准地的949株云杉解析木与其周围相邻木的最近距离对方程(9)进行拟合,得b=1.895,c=2.181,R2=0.996,即:

3.5 修正函数的确定
潜在生长量修正法是直径生长模型中最常用的方法[8,12]。首先确定林木的潜在生长量,建立疏开木的直径生长方程,然后用反映立地质量、林分密度、林木最近距离3个竞争指数所表示的修正系数建立修正函数。修正函数的合适与否主要取决于林木竞争指标选择和组合是否合理,这种方法构造的模型具有结构清晰的优点,而且只要正确选择疏开木,且所构造的竞争指标能充分有效地反映林木生长的变异,一般都能获得良好的预测效果。
修正函数MD应满足以下性质:
①随FCC的增加,单株树木的生长空间减小,其生长量随之减小,即修正函数MD是FCC的减函数,随FCC值的增加而减小[12]。
②立地条件越好,林地的生产力越高,修正函数MD与立地质量呈正相关。
③修正函数MD取值范围为:0≤MD≤1。
根据文献[8]、[12]和修正函数的上述性质可以通过指数函数和幂函数的组合形式确定修正函数。因此组合用数式表示有下列4种情况:

从理论上讲,地位级lgH、F(x)的取值范围在(0,1),且F(x)为常数。
3.6 胸径生长的多元回归模型
将直径潜在生长方程(方程3)和修正函数MD(方程11至14)代入直径预测模型D=MD·y中,则得到:
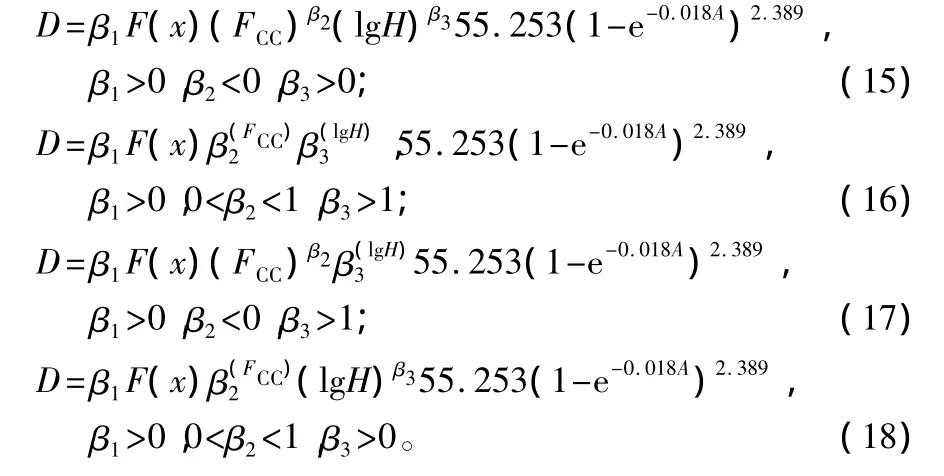
将公式(4)、(8)和(10)分别代入方程(15)至(18)后,采用SPSS软件,以长白山地区18块皆伐标准地的949株云杉解析木和78株云杉标准木,进行拟合,依据修正系数0≤MD≤1、相关系数最大和剩余平方和最小,可得方程(17)为直径实际生长的最佳回归模型,且参数分别为β1=1.235,β2=-0.090,β3=1.166;相关系数R2=0.931。即直径生长的多元回归预测模型为:

3.7 模型的检验
为了科学客观评价拟合效果,采用平均系统误差(E)、剩余标准差(S)和均方根误差(Δ)对模型进行检验。各公式如下:
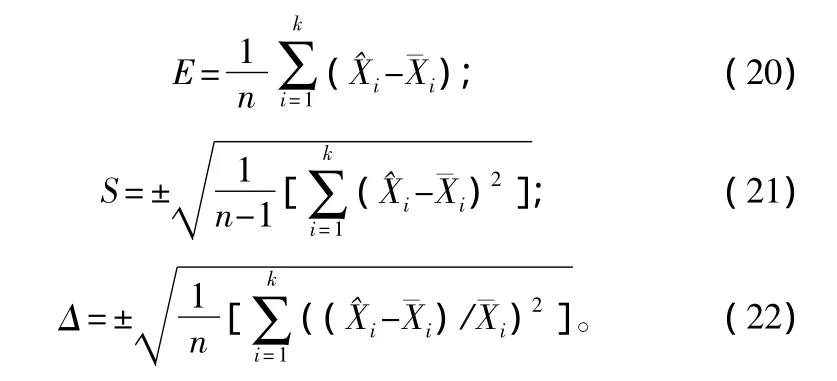
用未参加建模的8块皆伐标准地的432株云杉解析木和23株云杉标准木,对直径生长的多元回归预测模型的拟合度进行检验,即以皆伐标准地云杉实测直径与直径生长的多元回归预测模型计算得到的直径进行比较,得到平均系统误差的绝对值(|E|)=2.1%<5%,均方根误差(Δ)=5.6%<10%。这说明理论生长量与实际生长量差异不显著,直径生长的多元回归预测模型可用于预估林木直径的生长,且效果很好,预估的相对误差为4.52%,估计精度P为95.48%。该模型可以合理预测长白山地区主要树种林木的未来直径大小,这对把握林分动态和预估林分生长状态有极其重要的意义。
4 结论与讨论
长白山主要树种直径生长的多元回归预测模型为:D=1.235F(x)(FCC)-0.0901.166lgH55.253(1 -e-0.018A)2.389,对模型进行检验,结果显示其拟合效果很好。该模型可以合理预测长白山地区主要树种林木的未来直径大小。
本研究以云杉为例进行分析,对于长白山地区其它主要树种,如冷杉、红松和枫桦等,只要有足够数据,重新拟合求出各方程的参数,就可以对林木直径的生长进行预估。
在建立直径生长的多元回归预测模型时,假设环境条件一致,但从天然异龄林的整个生命过程来看环境因子不应该一直是不变的,因此本模型只适合预测阶段性林木直径结构,没有考虑采伐强度和采伐周期等因子的影响,在以后的研究中应予以考虑,进一步提高预估精度的准确性。
[1]孟宪宇.测树学[M].北京:中国林业出版社,2006.
[2]张青,赵俊卉,亢新刚,等.基于长期历史数据的直径结构预测模型[J].林业科学,2010,46(9):182-185.
[3]孟宪宇.使用Weibull函数对树高分布和直径分布的研究[J].北京林业大学学报,1988,10(1):40-48.
[4]亢新刚,胡文力,董景林,等.过伐林区检查法经营针阔混交林林分结构动态[J].北京林业大学学报,2003,25(6):1-5.
[5]胡云云,亢新刚,赵俊卉.长白山地区天然林林木年龄与胸径的变动关系[J].东北林业大学学报,2009,37(11):38-42.
[6]Bailey R L.Individual tree growth derived from diameter distribution models[J].Forest Science,1980,26(4):626-632.
[7]Liu C,Zhang L,Davis C J,et al.A finite mixture model for characterizing the diameter distribution of mixed-species forest stands[J].Forest Science,2002,48(4):653-661.
[8]孟宪宇,张弘.闽北杉木人工林单木模型[J].北京林业大学学报,1996,18(2):1-8.
[9]李凤日,吴俊民,鲁胜利.Richards函数与Schnute生长模型的比较[J].东北林业大学学报,1993,21(4):15-24.
[10]Krajicek J E,Brinkman K A,Gingrich S F.Crown competitiona measure of density[J].Forest Science,1961,7(1):35-42.
[11]王韩民,惠刚盈.林木最近距离分布模型的研究[J].林业科学研究,2005,18(5):556-560.
[12]励龙昌.以潜能函数建立单木生长模型[J].东北林业大学学报,1990,18(4):22-28.

