加筋圆环壳的理论求解及性能研究
邹 广,彭兴宁,杜青海
(中国船舶科学研究中心,江苏 无锡 214082)
1 引 言
随着世界各国对深海装备的发展及对深海资源的探索、开发与利用,典型柱和球型结构远不能满足此要求。圆环形结构为新型深海装备及水下运载器的发展展示了新的面貌和功能。然而环壳结构因其特有的结构形式,其理论研究乃至工程应用问题一直是理论界和工程界的一大难题。
至上世纪九十年代末,众多学者开展了环壳方面的研究工作,圆环壳轴对称线弹性问题基本得到解决,对这一问题做出突出贡献的有Clark[1]、钱伟长[2]等人,他们以圆环壳的复变量方程为基础得到了圆环壳的级数解,并证明了级数解的收敛性。对于承受任意非对称载荷的圆环壳,陈山林[3]采用Fourier级数法求解得到了比较完整且简单的解析解,张若京[4]选择广义Airy函数作为展开函数得到了全部4个基解和一个特解的完全渐近展开式。但是,他们研究的对象均是不含加强肋骨型材的纯圆环壳模型。
进入二十一世纪,英国学者Carl[5-6]在设计水下导弹发射基地和水下空间站时,建议在水下工程中使用圆环形耐压结构形式,便于实现特有功能。基于现代多功能新型水下运载器发展需要,杜青海等[7-8]结合环壳结构应用于水下工程的特点,运用数值方法分析了加筋圆环壳结构的线弹性及其非线性结构属性,从而论证了圆环壳结构可作为水下工程耐压结构主体构件的可行性。
本文在前期研究[7-8]的基础上,并充分考虑环向肋骨对圆环壳弯曲变形的约束影响,将加筋圆环壳在静水压力作用下的变形简化为两端刚性固定在弹性支座上的弹性基础曲梁的复杂弯曲问题来研究。同时基于弹性曲梁和薄壳理论,运用简化等效原则求解了加筋圆环壳结构关键截面处应力与位移的理论表达式,由此得到加筋圆环壳结构强度与变形简化理论计算方法。最后本文基于理论解,给出了加筋圆环壳结构典型关键点位置上的应力随其结构参数的变化规律,便于环壳结构设计及工程应用参考。
2 加筋圆环壳的结构参数
鉴于圆环壳结构运用于水下工程的特点,需在圆环壳外设置一系列具有一定刚度的环形肋骨,以提高壳体的稳定性。具有环形肋骨加强圆环壳的结构示意图如图1,各结构参数的意义如下:
R为弯曲半径 (大圆半径);a为截面半径 (小圆半径);φ为旋转轴与截面圆法线的夹角;θ为截面圆沿环向的旋转角度;t为壳板厚度;F为肋骨型材剖面积;θ0为相邻两肋骨夹角;l为肋骨间距,l=R·θ0。
3 圆环壳结构特性分析
运用薄膜理论可求得圆环壳的主应力

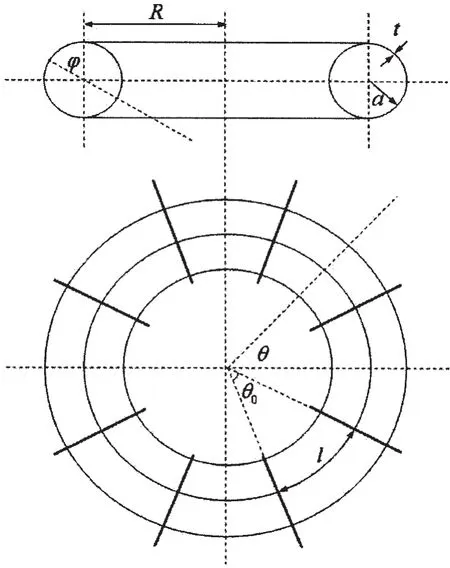
图1 加筋圆环壳结构示意图Fig.1 Structural diagram of a ring-stiffened circular toroidal shell
根据薄膜受力状态下圆环壳应力表达式,可以得出以下结论:
(1)环向应力σθ为常量,截面周向应力σφ随φ而变化。定义应力变异系数

图3给出了圆环壳外圈、内圈和顶圈(图2中BB′、DD′和AA′)应力变异系数k随相对弯曲半径R/a的变化规律,可以看出:① kin>2,随着R/a的不断增大,kin不断减小且逐渐趋近于2;② 当1<R/a<3时,kin的值减小得很快;③ 1.5<kout<2,随着 R/a的不断增大,kout缓慢增大且逐渐趋近于 2。
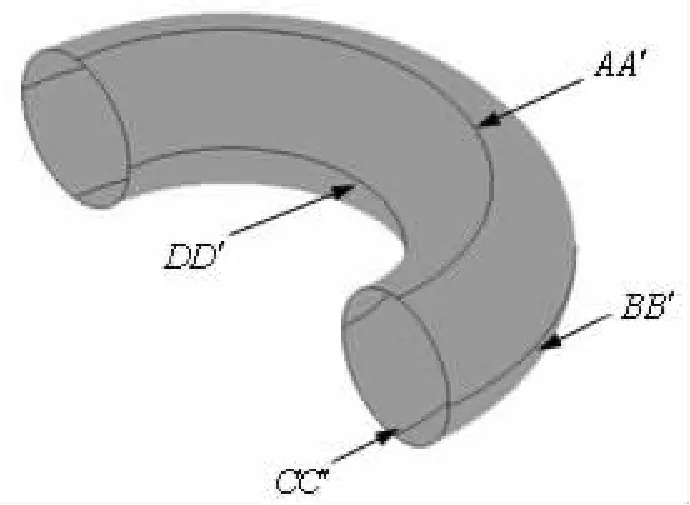
图2 圆环壳的典型位置Fig.2 Typical positions of a circular toroidal shell
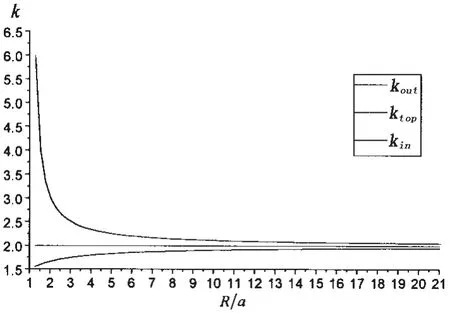
图3 典型位置应力变异系数k随R/a的变化曲线Fig.3 The variation curves of k with R/a
(2) 圆环壳 R/a>1,其外圈处 1.5<kout<2,内圈处 kin>2。 当 R→∞ 时,圆环壳趋近于圆柱壳,k=2;当R=0 时,圆环壳退化为球壳,k=1;当 0<R/a<1 时,壳体类似于南瓜形状,其外圈处 1<k<1.5。 因此,当旋转半径R不断变化时,应力变异系数k存在以下关系式:

4 加筋圆环壳结构强度的理论计算方法
4.1 加筋圆环壳的简化力学模型
当圆环壳受均匀压力作用时,由于结构和载荷都对称于旋转轴,在失稳之前壳的变形也必然对称于旋转轴。肋骨的存在约束了壳的压缩变形,壳受到肋骨的反作用力而在环向产生了弯曲,使得加筋圆环壳的强度问题不再是轴对称问题。但是由于加筋圆环壳的结构和载荷对称于每一肋骨断面,壳的变形也必然对称于每一肋骨断面,因而只需要研究其中的一个肋骨间距。这样使得加筋圆环壳的强度问题可归结为如图4所示的力学模型来研究,即按从圆环壳上截取的单位宽度的曲梁带来研究。
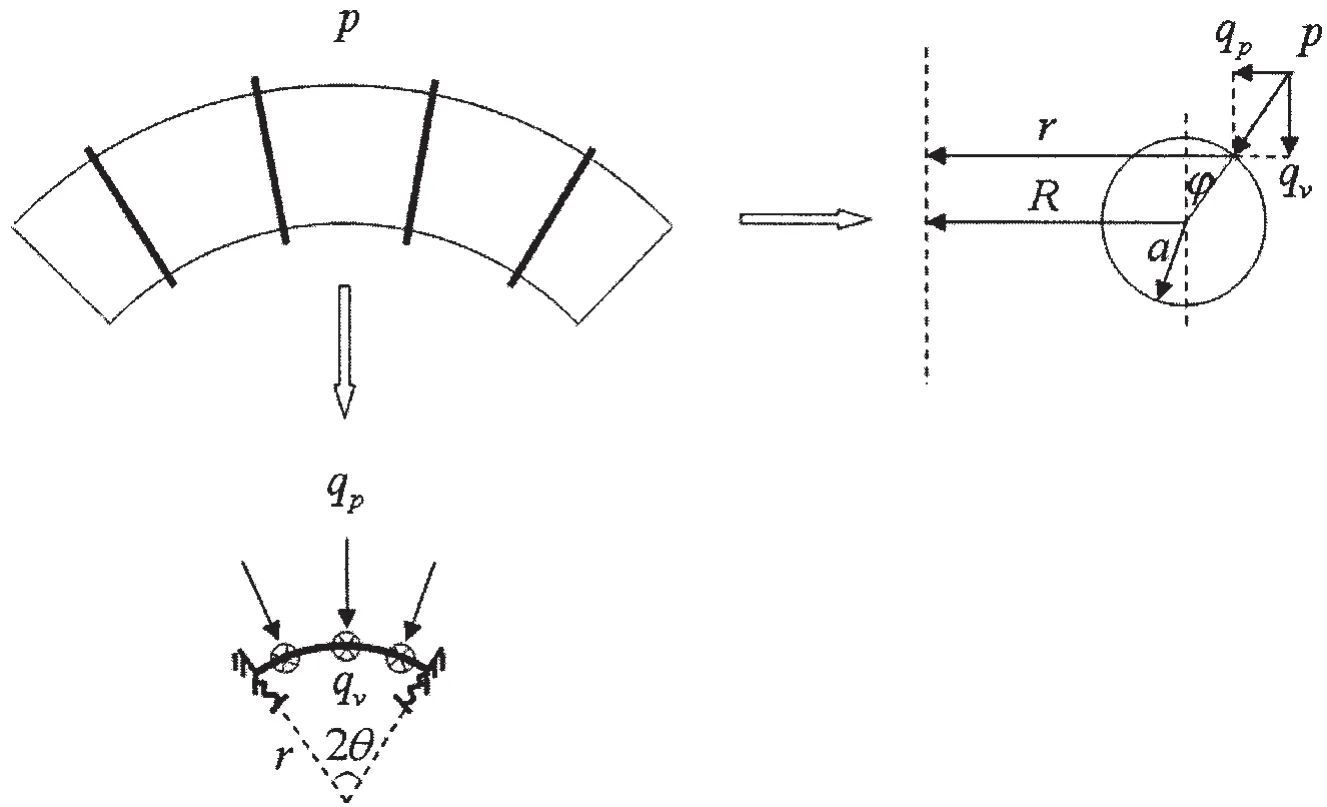
图4 加筋圆环壳的简化力学模型Fig.4 The mechanical model of a ring-stiffened circular toroidal shell
这种简化思想的关键点在于均布载荷p的分解以及曲梁曲率半径r的确定。如图4,可以将加筋圆环壳的变形化为位于该点所在纬线处曲梁的弯曲变形来研究,曲梁的曲率平面为该点处纬线确定的平面,曲率中心为曲率平面与旋转轴的交点,曲率半径为该点至旋转轴的距离,即

该点处的外载荷p可以分解为垂直于旋转轴的载荷分量qp和平行于旋转轴的载荷分量qv,其大小分别为其中载荷分量qp作用于曲梁的曲率平面内,载荷分量qv垂直于曲率平面。

加筋圆环壳外圈、内圈和顶圈(图2中 BB′、DD′和 AA′)对应的力学模型如图5,三者对应的曲梁的曲率半径、载荷大小及方向各不相同。表1给出了任意点及三个典型位置处简化的详细情况。根据这些简化力学模型,可以对加筋圆环壳进行理论求解。
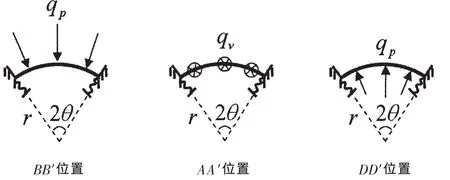
图5 典型位置对应的力学模型Fig.5 Mechanical models of typical positions

表1 加筋圆环壳简化模型的参数Tab.1 Parameters of the simplified mechanical models
本文具体以外圈和内圈为例介绍这种求解方法,计算模型分别为图5中(a)和(c),曲梁的曲率半径分别为r=R+a、r=R-a,外载荷分别作用于曲梁的外表面和内表面。
4
.2圆环壳曲梁带的弯曲微分方程
根据加筋圆环壳的受力情况,作用于圆环壳外圈曲梁带(图5中BB′位置)上的力有:
(1)作用在梁带外表面上的均匀正压力qp=p;
(2)由于壳体压缩变形,在梁带内引起轴向压缩力T1;
(3)作用在梁带两侧边界上的梁带之间的相互作用力T2。
数值分析发现加筋圆环壳旋转方向的中面应力在一个肋骨跨度内变化极小,且与圆环壳的薄膜理论解非常接近,因而可取曲梁轴向压缩力

图6 梁带的受力Fig.6 Forces on a curved beam

T2的合力方向与法向外压力的方向一致,因此应将该力包括在梁带所受的外载荷中。如图6所示,单位宽度梁带上的载荷总强度为

T2是一个超静定力,其大小可以通过变形几何关系和胡克定律得到:

由(6)、(7)和(8)式得

由上述分析知,图5中(a)所示力学模型同时受到横载荷q及轴向力T1的作用,处于复杂弯曲状态。如图7,用两个无限接近垂直于中和轴的剖面从图5中(a)所示曲梁上分割出一个微元(距离为
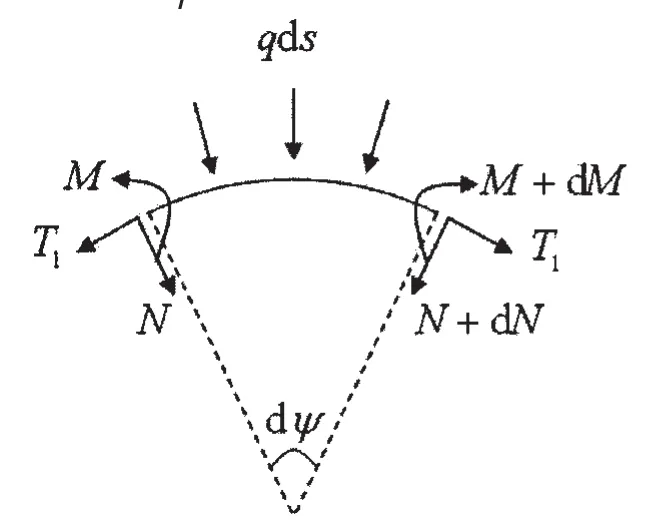
图7 曲梁微元Fig.7 A curved beam element
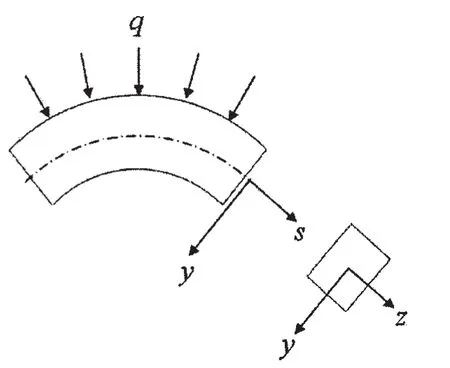
图8 坐标系Fig.8 Coordinate
去掉高阶无穷小量,曲梁微元的静力平衡方程可表示为:若规定弯矩M的正向如图8中所示,则梁断面上的弯矩


将(6)、(9)和(11)式代入方程组(10),经整理可得到曲梁带的微分平衡方程:

加筋圆环壳内圈对应力学模型如图5(c)所示,它与图5(a)所示力学模型的区别在于竖直方向的受力平衡方程(10)应改为
式中:r=R-a。
因而加筋圆环壳内圈曲梁带的微分平衡方程应为:


4.3 曲梁带的边界条件
根据加筋圆环壳的受力及变形特点可以得到曲梁的边界条件。由于加筋圆环壳的变形对称于每一肋骨断面,因而在肋骨断面处壳的转角为零,即

这是一个边界条件,另一个边界条件可通过研究壳体与环肋间的相互作用得到。通过分析发现在环肋处,有:

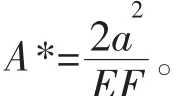
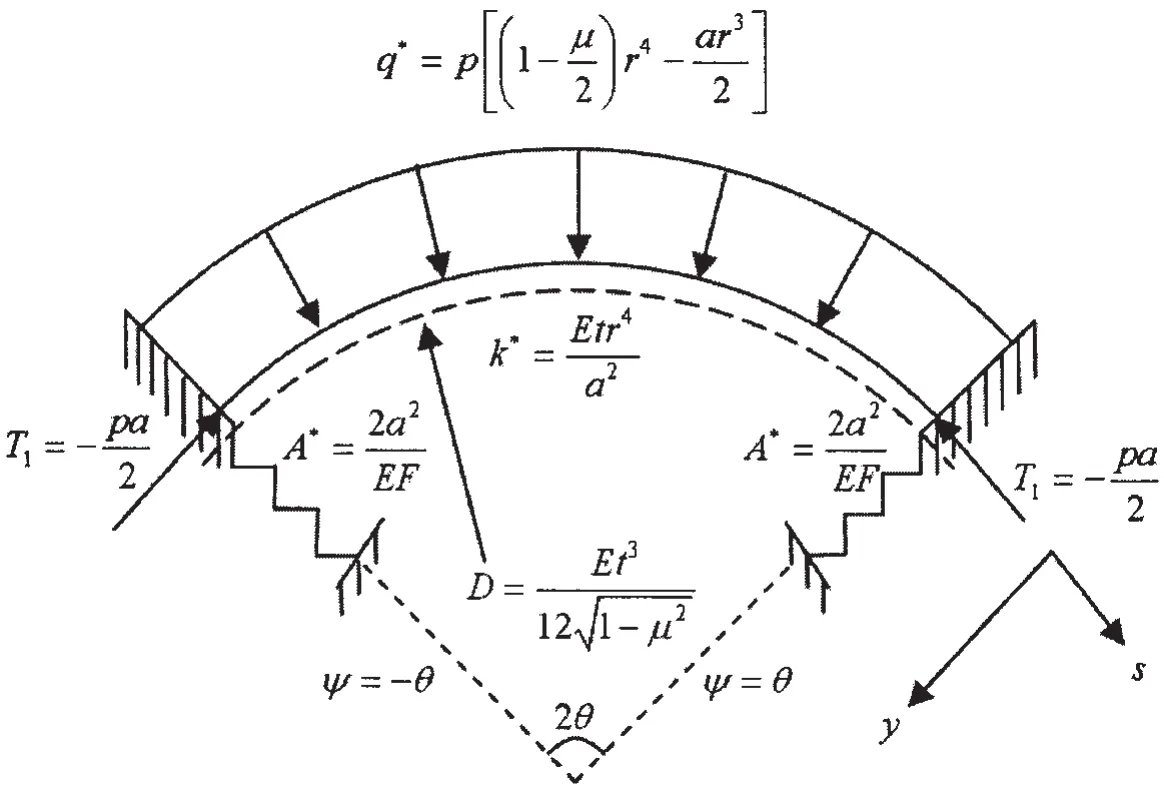
图9 加筋圆环壳的简化力学模型Fig.9 Simplified mechanical model of a ring-stiffened circular toroidal shell

从而图5中BB′所示圆环壳曲梁带的边界条件可表示为:
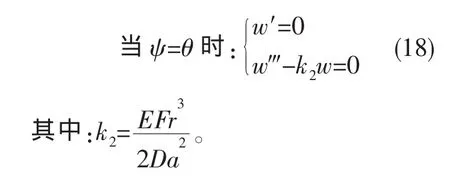
由(6)、(10)和(11)式得
将曲梁带的弯曲微分方程式(12)和边界条件式(18)综合来看,以一系列等间距同刚度环肋加强的圆环壳,在均匀外压作用下的变形,可以化为两端刚性固定在弹性支座上的复杂弯曲弹性基础曲梁来研究。可以简单地用如图9所示的力学模型来概括。
4.4 加筋圆环壳典型位置应力和位移表达式
非齐次方程(12)和(14)的通解为
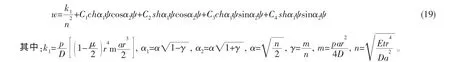
将坐标原点设在肋骨跨度中点处,由于圆环壳在环向的弯曲对称于坐标原点,因而

将通解式(19)代入边界条件式(18),即可求得积分常数

将积分常数回代入通解式,即可求得曲梁带的挠度w,并由此求得圆环壳外圈及内圈各弯曲要素。
(1) 挠度
将ψ=θ和ψ=0代入微分方程通解式(19),即可求得壳体的挠度。
跨度端部:

跨度中点处:

(2) 环向应力
壳体环向应力由沿厚度均匀分布的膜应力及沿厚度按线性规律分布的弯曲应力组成。跨度端部:

跨度中点处:

(3)截面周向应力
壳体处于双向应力状态,由物理方程即可求得壳体截面周向应力:跨度端部:
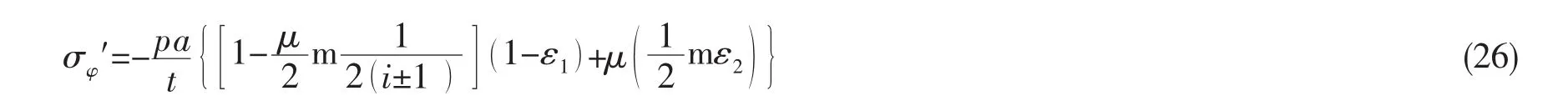
跨度中点处:

(4) 肋骨应力
肋骨处于单向应力状态,它与σθ的大小无关。肋骨应力
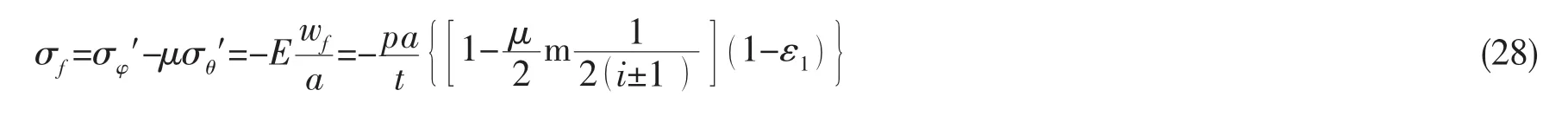
5 数值计算方法的验证
本文采用的计算模型如图10所示,取7个完整肋骨跨度进行计算,两端各留半个跨度,取最中间一个肋骨跨度的计算结果,计算模型的结构参数见表2。计算载荷取p=10MPa,E=1.96×105MPa,μ=0.3。
本文所得理论解与有限元数值解的比较见图11(外圈)和图12(内圈),分别比较了加筋圆环壳外圈和内圈处的弯曲应力、环向应力和周向应力。其中θ表示圆环壳两肋骨间夹角的1/2,ψ表示圆环壳外圈和内圈跨度内任意一点与跨度中点之间相对于旋转中心的夹角。比较结果显示在整个肋骨跨度内,本文所得理论解和有限元数值解吻合较好,从而验证了本文理论方法的正确性。表3对加筋圆环壳外圈和内圈跨度中点处及跨度端部环向应力、周向应力、肋骨应力的理论值及有限元值进行了比较,并进行了误差分析。

图10 计算模型Fig.10 The calculated model

表2 计算模型的结构参数Tab.2 Structural parameters of the calculated model
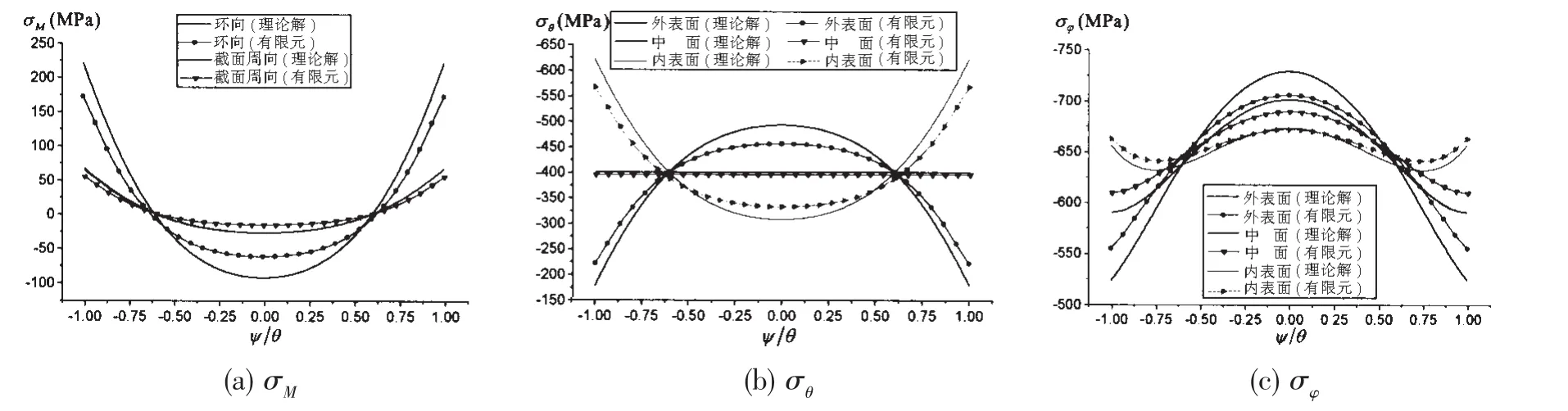
图11 理论解与数值解的比较(外圈)Fig.11 Comparison of the theoretical solution and the numerical solution(outside circle)

图12 理论解与数值解的比较(内圈)Fig.12 Comparison of the theoretical solution and the numerical solution(inside circle)

表3 理论解与数值解的比较(中面)Tab.3 Comparison of the theoretical solution and the numerical solution(middle layer)
6 加筋圆环壳结构特性分析
定义应力集中系数

分析无量纲结构参数R/a、β对外圈和内圈处的环向应力集中系数kc、周向应力集中系数kt及肋骨应力集中系数kf的影响。对于环向应力和周向应力各取两个部位:跨度端部壳内表面、跨度中点壳外表面。因为这两个部位的应力绝对值最大,是强度校核的重点。
6.1 参数R/a对应力的影响
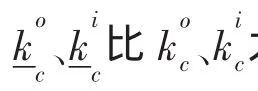
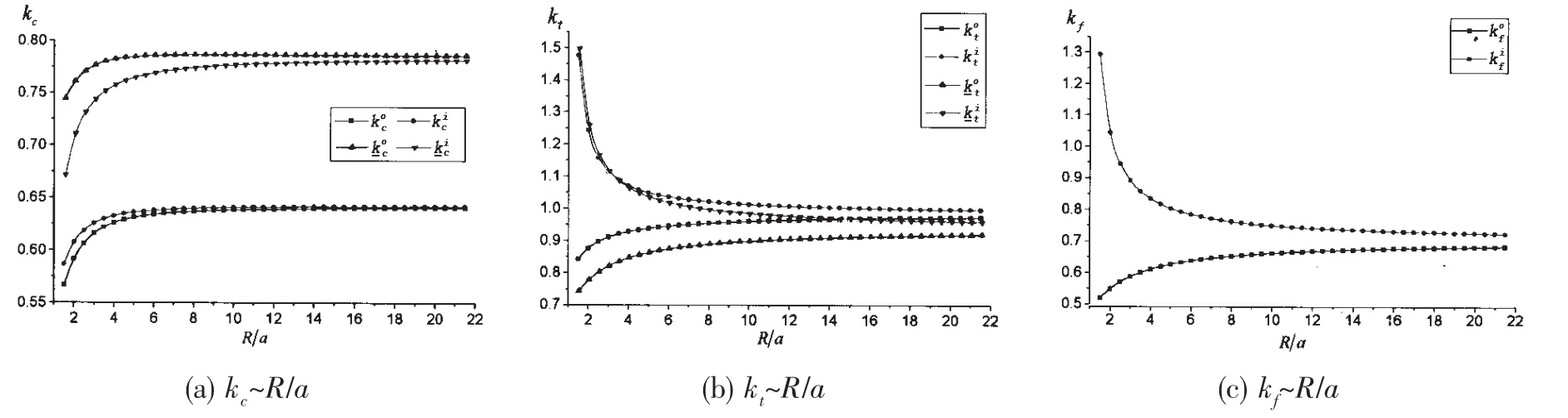
图13 参数R/a对应力集中系数的影响Fig.13 The effect of R/a on SCFs
6.2 参数β对应力的影响
参数β=(1±1/i) lt/F=l*t/F为一个跨度上壳板剖面积l*t和肋骨型材剖面积F的比值。如无肋骨,则1/β=0,可采用圆环壳的薄膜理论解计算。将薄膜理论解与本文理论解对比可以看出,应力集中系数ki实际上表明肋骨存在对壳板应力的影响。参数β越小,即肋骨越大,这个影响也越大。
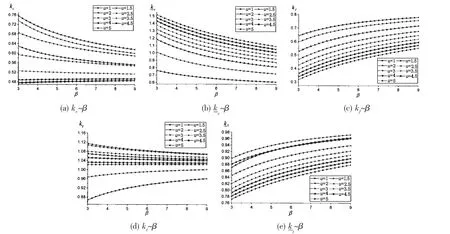
图14 参数β对应力集中系数的影响Fig.14 The effect of β on SCFs

7 结 论
本文基于弹性曲梁及薄壳理论,运用简化等效原则,开展了加筋圆环壳结构强度的理论求解工作,并从理论上和数值方法上分别进行了变参数下的结构特性分析。通过有限元数值方法验证了本文所给理论方法的正确性,为环壳结构的工程应用提供了理论基础。
本文所给加筋圆环壳理论计算方法是加筋圆柱壳理论计算方法的推广,加筋圆柱壳理论解是本文所给加筋圆环壳理论解当R/a→∞时的特例。
[1]Clark R A.On the theory of thin-walled toroidal shells[J].J Math and Physics,1950(29):146-178.
[2]钱伟长,郑思梁.轴对称圆环壳的复变量方程和轴对称环壳的一般解[J].清华大学学报,1979,19(1):27-47.
[3]陈山林.圆环壳在一般载荷下的轴对称问题[J].应用数学和力学,1986,7(5):425-434.
[4]张若京,张 维.承受非对称载荷圆环壳的完全渐近解[J].中国科学,1995,25(6):614-619.
[5]Ross Carl T F.A conceptual design of an underwater missile launcher[J].Ocean Engineering,2005(32):85-99.
[6]Ross Carl T F.A conceptual design of an underwater vehicle[J].Ocean Engineering,2006(33):2087-2104.
[7]Du Qinghai,Wan Zhengquan,Cui Weicheng.A study on structural characteristics of the ring-stiffened circular toroidal shells[C]//2nd International Conference on Marine Structures-Analysis and Design of Marine Structures.Lisbon,2009.
[8]Du Qinghai,Cui Weicheng,Wan Zhengquan.Nonlinear finite element analysis of a toroidal shell with ring-stiffened ribs[C]//Proceedings of the ASME 2010 29th International Conference on Ocean,Offshore and Arctic Engineering.Shanghai,2010.

