船用齿轮箱刚度评价方法的研究
杜雪松,朱才朝,刘伟辉,宁 杰
(1重庆大学机械传动国家重点实验室,重庆 400030;2杭州前进齿轮箱集团有限公司,杭州 311203)
1 引 言
船用齿轮箱是船舶动力系统的重要设备之一,结构复杂,承载能力和运转精度要求高。传动系统的刚度对其使用性能有重大的影响,在传动过程中,如果系统刚度不够会产生较大的动载荷和振动噪声,导致传动系统本身的破坏和故障。因此研究齿轮箱传动系统较为精确的刚度分析及量化评价方法,具有十分重要的意义。目前工程中一般都是对齿轮箱传动系统中各主要零部件单独进行刚度分析及评价,而非基于整个传动系统的综合分析。这一方法存在以下缺点:一是各零部件在传动过程中,其变形既可能相互叠加也可能相互补偿,上述方法无法揭示这种关系,也无法判断其对系统刚度的影响程度,因而也就无法对传动系统的刚度做出准确的评价;二是对于箱体这类结构复杂的零件,由于缺乏相关的标准作为评价依据,单独分析时只能基于简化的力学模型进行估算,或通过有限元法进行计算,然后根据经验进行定性评价,难于保证分析的准确性[1-4]。
针对上述问题,论文以船用齿轮箱为研究对象,以使用性能和相关技术条件为依据,综合考虑齿轮、轴、轴承和箱体的变形及其在运转过程中的相互关系,提出了一种较为精确的船用齿轮箱传动系统刚度分析及量化评价方法。
2 船用齿轮箱刚度评价方法
对于船用齿轮箱而言,保证齿轮具有良好的啮合状态以及输入输出联轴器正常工作至关重要。我国相关标准给出了船用齿轮箱输入输出联轴器的圆跳动(表1)和齿轮副齿向接触斑点技术条件(表2)[5]。这两类指标给齿轮箱传动系统刚度评价提供了基本依据。

表1 船用齿轮箱输入、输出联轴器的技术条件Tab.1 Specifications of Input/Output coupling of marine gearbox

表2 齿轮副齿向接触斑点技术条件Tab.2 Specifications of tooth contact pattern
2.1 基于联轴器技术条件的刚度校核
实践表明,运转过程中各零部件的受热及受载变形都会导致两轴轴线产生附加偏移,从而影响联轴器的工作平稳性和使用寿命[6]。因此,在实际工程中,安装调整后轴间的相对位移量通常只取许用值的1/2~1/3,剩余的许用偏移量用于补偿运转时联轴器的附加偏移量。图1为附加偏移量计算简图。图中的水平轴线为经安装时初步和精确找正后的轴线。轴受载挠曲,使位置1的联轴器产生角度偏移。同时,轴的轴向窜动,使联轴器到达位置2。此时,联轴器的径向圆跳动值为

则基于联轴器径向圆跳动的刚度校核式可以表示为:


图1 联轴器的偏移Fig.1 Offset of coupling
式中δ为联轴器的轴向串动量,θ为联轴器的偏转角,Δr[]为联轴器的许用径向圆跳动,按表1选取。δ与轴向载荷及轴承、轴承座刚度有关,将轴承和轴承座看成串联的弹簧,可得

式中FA为轴所受轴向力,KAb为轴承的轴向刚度,KAB为轴承座的轴向刚度。由图1的几何关系还可以得到联轴器的最大端面圆跳动为

式中D为联轴器直径。
考虑到标准中是以φ100处的端面圆跳动值为基准,经过换算后基于联轴器端面圆跳动的刚度校核式为

式中 Δa[]为联轴器的许用端面圆跳动,按表1选取。
(2)、(5)式中的θ与轴及支承的变形有关。对于安装齿轮的轴,其变形包括轴自身在载荷作用下的变形,以及由于支承的变形反映在轴上的变形。将轴的支承简化成串联的弹簧(图2),弹簧的刚度分别是轴承和轴承座的径向刚度,则

图2 联轴器的偏转角Fig.2 Deflection angle of coupling

式中θa为轴挠曲引起的联轴器的转角,θb为支承变形引起的联轴器的转角。
θa可根据弹性力学变截面梁弯曲理论进行计算,θb可由(7)式计算。

式中Δb1,Δb2分别为轴两端支承的变形。θb计算值为正表明彼此间是叠加关系,为负则表明是补偿关系。

式中λb、λB分别为轴承和轴承支座的径向变形。
由于箱体的形状较为复杂,因此(8)式中的λB一般应通过有限元分析得到。λb与轴承的刚度和所受载荷有关。由于轴承刚度具有明显的非线性,且初始和装配时的工艺参数(预紧量、初始游隙等)对其值也有显著影响,故要对运转条件下的轴承刚度进行准确计算较为困难。实际应用中,可对轴承刚度进行近似计算[7]。对于船用齿轮箱常用的圆柱滚子轴承,其径向刚度可按(9)式计算,受径向和轴向联合载荷作用的双列球面滚子轴承的径向及轴向刚度可按(10)、(11)式计算。

以上三式中Q0为轴承中受载最大滚动体所受载荷,Z为滚动体数目,l为滚动体长度,α为公称接触角,Jr、Ja为计算系数,与轴向力和径向力的比值有关,可通过迭代计算得到。
2.2 基于齿轮齿向接触斑点技术条件的刚度校核[8]
根据齿轮齿向载荷分布系数计算理论,齿轮啮合时的有效接触宽度bcal可通过以下方法计算:

否则

两式中Fm为分度圆上平均计算切向力,b为齿宽,Fβy为跑合后啮合齿向误差,cγ为轮齿啮合刚度。
在齿轮强度计算的有关标准中,均是在假定箱体、轴承的刚度足够大,忽略其变形的前提下给出Fβy计算公式的。但实践表明,船用齿轮箱(尤其大功率条件下)的箱体及轴承的变形对齿轮齿向载荷分布有非常明显的影响,要准确计算bcal,必需要计及箱体、轴承的变形影响。因此Fβy的计算式可修正为

式中fsh为轴和齿轮的变形引起的啮合齿向误差,xβ为齿向跑合系数,fsh、xβ的计算可参考相关标准。fP为考虑箱体、轴承变形引起的啮合齿向误差,由(15)式计算。

式中Fβ为齿向误差,fP1、fP2分别为一对啮合齿轮由箱体、轴承变形引起的啮合齿向误差,由(16)式计算。

式中Δb1,Δb2分别为两端支承的总变形,可参考(8)式计算,L为支点间距。
以上两式中的正负号表明了各计算量间是相互叠加还是补偿的关系,与齿轮相对与支承的布置方式以及支反力方向等因素有关,计算时需根据具体情况做详细分析。
将(12)、(13)式两端同除以b,得到基于齿向接触斑点技术条件的刚度校核式为:

否则

两式中 [b′cal]为齿轮副的齿向接触斑点许用值,可由表2查取。
3 算 例
某船用齿轮箱传动系统简图如图3所示。箱体材料为HT250,计算时取弹性模量E=120 GPa、泊松比μ=0.26。传动比i=1.976 2,输入轴转速n1=400r/min,传递功率P=7 695 kW,传递能力19.2 kW/(r·min-1)。所有齿轮均为斜齿圆柱齿轮。根据输入轴转向不同,计算共分为两种工况(从输出端看,输入轴逆时针转动为工况1,顺时针转动为工况2)。输入轴输入端(靠近联轴器一端)采用圆柱滚子轴承,输出端(远离联轴器一端)采用球面滚子轴承。
根据(9)~(11)式计算得到输入轴轴承刚度及变形量(表 3)。
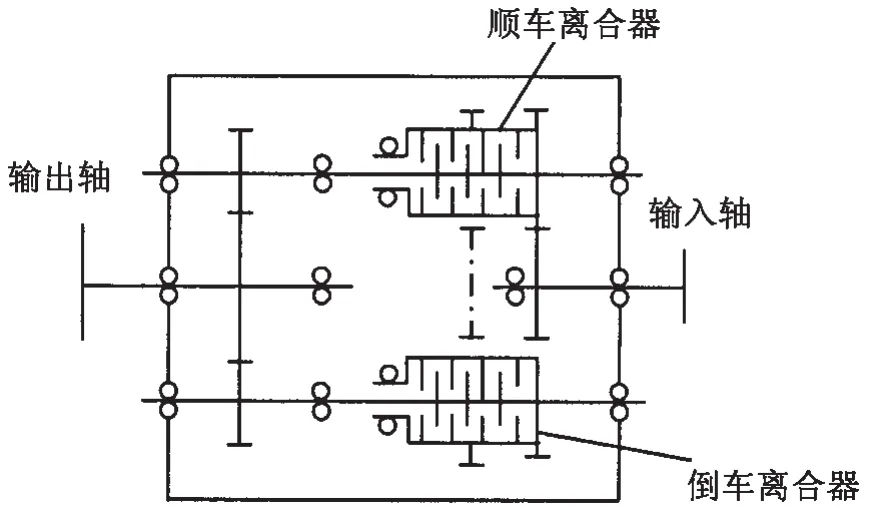
图3 传动系统简图Fig.3 Sketch of transmission system

表3 输入轴轴承的刚度及变形量Tab.3 Stiffness and deformation of input shaft bearing
箱体有限元模型如图5所示,下箱体两侧翼底面作固定约束,上中下箱体的各接触面间选用绑定接触类型以加快计算。采用20节点六面体单元,模型共计221 177个节点,67 096个单元。忽略轴承套圈的倾斜,则各滚动体所传递的轴向负荷相同,故轴向载荷可按均布载荷加到箱体轴承孔端面上;径向载荷通过轴承传递到箱体时,只有部分滚动体承受载荷,其负荷分布区夹角与滚动体数目、径向游隙等因素有关,在负荷分布区内,可将径向载荷按余弦分布规律加到箱体轴承孔上(图4),载荷密度(不计径向游隙)按(19)式确定[9]。
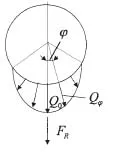
图4 轴承孔径向载荷的分布Fig.4 Radial load distribution of bearing housing

图4 轴承孔径向载荷的分布Fig.4 Radial load distribution of bearing housing
式中Qφ为与径向载荷FR成φ角位置的载荷密度,Q0为受载最大滚动体载荷,1/t的取值,对球轴承为3/2,滚子轴承为1.1,h为箱体轴承孔长度。
图6和图7为两种工况下箱体的综合位移图。轴承座的变形量及刚度见表4。从表中可以看出,轴承座径向刚度在不同工况下其值相差较大(输入端相差约38.3%,输出端相差约33.4%),这是由于工况不同,轴承座上的径向力大小和方向也不同。同时,加强筋位置和结构尺寸等因素使得轴承座在圆周方向并不完全对称,从而造成不同工况下轴承座的径向刚度不等。轴向刚度在两种工况下基本相同,因为两种工况下轴向载荷大小相等,仅方向相反,而承载结构又基本相同。

图5 箱体有限元模型Fig.5 Finite element model of gearbox

图6 工况1箱体综合位移 Fig.6 Total deformation of gearbox under No.1 conditions

图7 工况2箱体综合位移Fig.7 Total deformation of gearbox under No.2 conditions

表4 输入轴轴承座的刚度及变形量Tab.4 Stiffness and deformation of input shaft bearing housing
由(6)式计算得到联轴器总转角(表5),由(12)~(18)式计算得到输入齿轮副的齿向接触斑点值(表6),由(2)式,计算得到联轴器的径向圆跳动值(表7)。从表中的数据可以看出,在两种工况下,输入轴处径向和轴向刚度均满足要求。

表5 联轴器总转角Tab.5 Total rotation angle of coupling
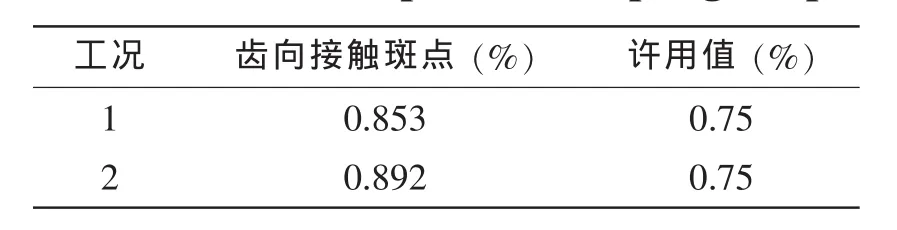
表6 输入齿轮副的齿向接触斑点 Tab.6 Tooth contact pattern of input gear-pair

表7 联轴器的径向圆跳动Tab.7 Radical circular run-out error of coupling
以上介绍了齿轮箱输入轴部分的刚度分析及评价。船用齿轮箱一般为多级齿轮传动,因此对其输出轴及中间轴部分也要进行类似的分析,限于篇幅,此处从略。
4 结 论
综合考虑轴、轴承、齿轮和箱体等主要零部件的变形及其在传动过程中的相互影响,基于船用齿轮箱技术条件中的相关指标,提出了一种较为精确的船用齿轮箱传动系统刚度评价新方法。与传统方法相比,新方法不但可以对箱体进行刚度量化评价,避免根据经验定性评价,为箱体的结构优化提供计算依据,而且对整个传动系统的刚度分析及评价更为合理和准确。计算表明,箱体由于结构复杂,不同工况下其变形及刚度也不相同,从而使各零部件间的变形并不是稳定的叠加或补偿关系,而是随工况的不同而改变。这有可能导致在某些工况下箱体变形量较小,但传动系统的变形由于叠加关系反而较大,因此在对箱体进行刚度分析时,应针对全部工况进行。
[1]成大先.机械设计手册(第5版)[M].北京:化学工业出版社,2008.
[2]杨文硕,满志强.齿轮减速箱体的结构力学分析[J].哈尔滨科学技术大学学报,1995,19(3):94-98.
[3]Ramamurti V,Gautam P,Kothari A.Computer-aided design of a two-stage gearbox[J].Advances in Engineering Software,1997,28:73-82.
[4]Li Runfang,Yang Chengyun,Lin Tengjiao.Finite element simulation of the dynamical behavior of a speed-increase gearbox[J].Journal of Materials Processing Technology,2004,150:170-174.
[5]JB/T 9746.1-1999,船用齿轮箱技术条件[S].1999.
[6]刘占生,赵 广,龙 鑫.转子系统联轴器不对中研究综述[J].汽轮机技术,2007,49(5):321-325.
[7]丁长安,常 瑭.滚子轴承受载变形计算的修正[J].轴承,2007(8):1-4.
[8]张 涛,冯守卫,濮良贵,方宗德.齿轮轮齿刚度与齿间载荷分配系数的再研究[J].西安公路交通大学学报,1999,19(4):112-116.
[9]邓四二,贾群义.滚动轴承设计原理[M].北京:中国标准出版社,2008.

