压电层合柔性梁振动主动控制
洪 明,陈 凤
(大连理工大学 工业装备结构分析国家重点实验室 运载工程与力学学部 船舶工程学院,辽宁 大连116024)
1 引 言
随着科学技术的发展,具备低质量、宽频带和强适应性等特点的智能材料势必在舰船等结构振动控制中得到越来越广泛的应用。对含压电层的柔性智能结构振动控制的研究,也是为提高舰船结构性能做技术储备。
国内外已经有很多学者研究了压电层合结构的力学行为及其振动控制[1]。Edward[2]介绍了压电作动器作为智能结构单元的分析和实验的发展,基于Bernoulli-Euler梁假设分析了表面粘贴或内部嵌入有压电层的悬臂梁的力学模型,并与实验结果对比。Tzou[3]提出了一种包含电势自由度的有限元模型,并采用该模型分析了一个具有分布式压电传感器和作动器的平板的动力性能。Ray[4]精确求解了四边简支压电层合矩形板的静力问题,并探讨了作动器和传感器能产生和感应变形的能力。Samanta[5]基于剪切变形理论提出了一种8节点四边形等参单元,并用速度负反馈控制对有分布式压电传感器和作动器的层合板进行主动控制。Sung[6]采用包含电势自由度的20节点体单元分析了压电结构的非线性动力响应。Simoes-Moita[7]基于经典的Kirchhoff理论,通过Hamilton原理建立了3节点三角形单元的压电层合板的有限元方程,并采用常增益速度负反馈控制抑制了受脉冲或简谐激励下简支梁的振动。Narayanan[8]在有限元方程中考虑了温度对机电特性的影响,比较了结构承受脉冲或简谐激励下常增益速度负反馈控制、Lyapunov反馈控制以及LQR最优控制。Jiang[9]基于高阶位移场、高阶电势场以及线性温度场,通过广义虚功原理推导了一种2节点含分布式压电传感器和作动器的压电热弹性复合梁的有限元模型,采用常增益速度负反馈控制抑制了结构受脉冲激励或温度激励下的振动。Pietrzakowski[10]假设电势沿厚度方向的分布是余弦函数和线性函数的组合,探讨了压电柔性结构的振动主动控制。
本文采用4节点四边形等参单元模拟上下表面分别粘贴有分布式压电作动器和传感器的层合板/壳单元。每个节点含有6个广义位移自由度,对应每个压电层再引入一个电势自由度。基于Mindlin一阶剪切变形理论,通过Hamilton原理建立有限元方程,用精细积分法得到系统状态空间响应,基于线性二次型输出调节器问题设计控制器,然后编制相应的有限元程序,实现压电层合悬臂梁的振动主动控制。
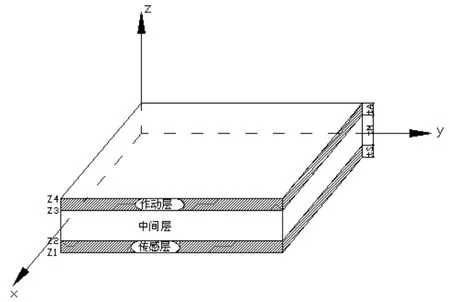
图1 压电层合单元节点坐标示意图Fig.1 Coordinate of the piezoelectric laminated element
2 压电层合单元有限元模型推导
2.1 基本假设
单元模型为上下表面分别粘贴有压电层的板壳结构,如图1所示。各层均满足弹性力学基本假设,压电层沿z向极化,电势沿厚度方向线性分布。
实际上,压电材料都是各向异性的,各向同性的材料不可能产生压电。Kepler[11-12]研究的单向或双向拉伸的PVDF认为在xy平面内弹性模量E相等,满足这样特性的材料的方程就跟各向同性材料是一样的。由于压电聚合物的杨氏模量一般比所关心的结构的杨氏模量小10倍以上,因此即使对于机械各项异性的压电材料得到的近似结果也是很精确的[13]。假设压电层与板之间为理想粘贴,不考虑粘贴层的影响。
2.2 位移场和应变场
根据Mindlin一阶剪切变形理论,压电层合单元中任意一点(x,y,z)的位移表示如下:

其中, (u0,v0,w0)为该点在中性面投影点 (x,y,0)分别在x、y和z方向的位移,θx和 θy分别为关于x轴和y轴的转角。
2.3 几何方程
根据弹性力学基本方程,令σz=0,可得到如下几何方程表达式:

记作:

单元中任意一点的应变ε可以表示为:

2.4 压电本构方程
对于各向同性的压电薄层,Tiersten[14]给出其本构方程的形式为:

其中,σ和ε分别为压电层的应力和应变矢量,Q为压电层弹性矩阵,e为压电应力常数矩阵,E为电场矢量,D为电位移矢量和P为介电常数矩阵。
电场与电势的关系可表示为E=-▽φ,压电层沿厚度方向极化,则有E= { 0 0 -Ez}T,其中 Ez=-φ/t,φ为压电层上下表面的电势差,假设它沿厚度方向线性变化。

对于含有多层压电层时,电场与电势的关系可表示为:


2.5 压电层合单元有限元方程
通过Hamilton原理得到压电层合板的动力方程:
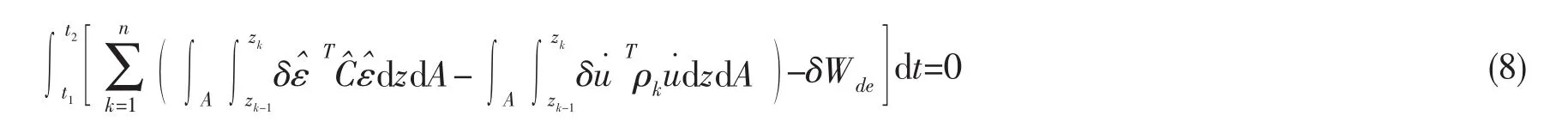
式中三项分别表示系统的应变能、动能和外力做功的变分。外力做功为:

其中,fv为体力,fs为面力,fci为第i个节点的集中力,q为压电层表面电荷。
本文采用的是双线性4节点四边形等参单元,每个节点5个广义位移自由度,另外每个单元每层压电层有1个电势自由度。位移插值函数如下式:


坐标变换后组装系统总刚度阵和总质量阵,得到系统方程为:

t表示作动器的作用电势的等效力。
3 压电层合柔性结构状态空间方程
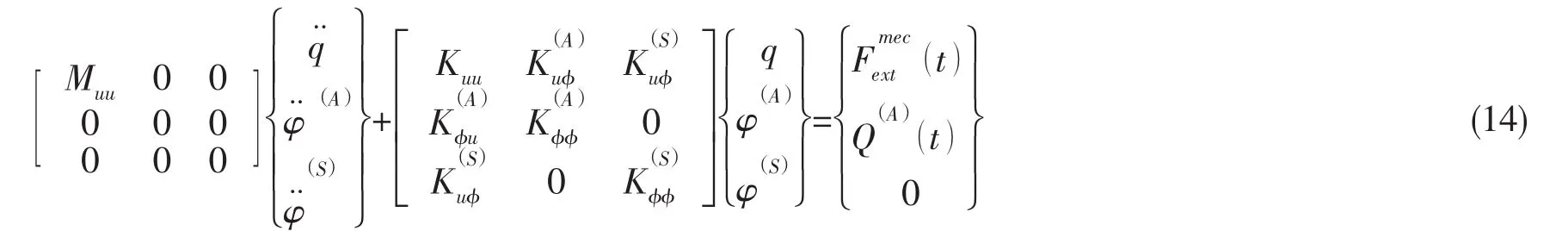
上式展开为:
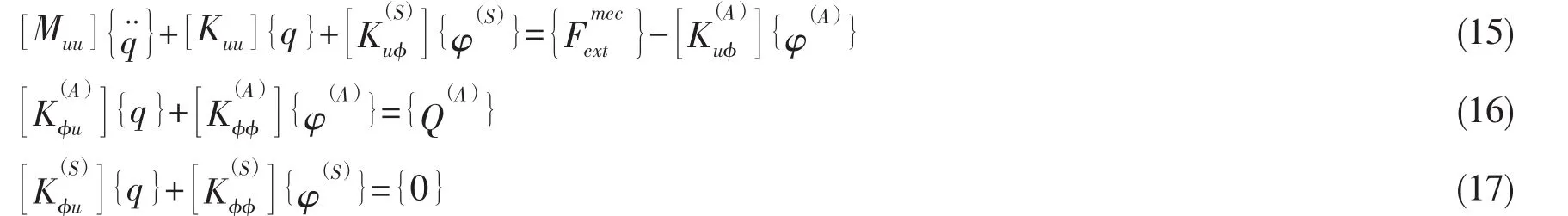
由(17)式可以得到传感层的输出电势为:

将(18)式代入(15)式,并用[M ]代替 [Muu],可得到系统无阻尼自由振动方程为:

对应的有阻尼强迫振动方程为:
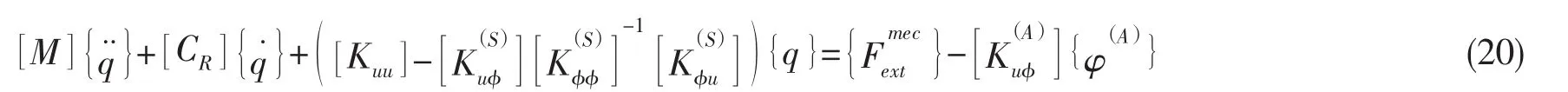
将(20)式转化到状态空间为:

用精细积分法求解方程(21)即可得到系统的状态空间响应。
4 线性二次型输出调节器
根据最优控制线性二次型输出调节器问题,控制目标函数选为传感器输出以及作动器控制电势的二次加权和。

其中,权系数矩阵Q为半正定对称阵,R为正定对称阵。在LQR控制器的设计中,Q和R的选择对于最优控制的结果具有很大的影响。在实际工程中,为简化最优控制问题的计算,通常选R为单位矩阵,Q为对角阵,只需调整Q即可。
反馈控制电势满足:

其中GA为反馈增益,满足:

式中P为代数Riccati方程(26)的解。

同样用精细积分法求解代数Riccati方程。将(23)式和(24)式代入方程(21),得到考虑LQR控制后的状态空间方程组为:

5 压电层合悬臂梁振动控制数值模拟
基于上面相应的理论,本文采用FORTRAN语言编制的计算机程序,首先计算悬臂梁承受电载荷时的变形,与参考文献比较,验证本文所推导的压电层合单元的正确性。然后采用计算精度较高的精细积分算法的HPD_S格式求解方程(21),计算结构受简谐激励或脉冲激励下的状态空间响应。同样用精细积分法求解最优控制中的Riccati方程,得到控制增益,求解考虑控制后的状态空间方程(26),得到不同的权系数矩阵下控制后的系统响应,与控制前的响应形成对比,比较控制效果。
5.1 压电层合单元模型验证
首先根据Tzou[15]的实验,验证前面所推导的压电层合单元的正确性。实验是由如图2所示两层极化方向相反的PVDF粘贴成的悬臂梁,压电层材料参数如表1所示。

图2 压电层合悬臂梁有限元模型Fig.2 Finite element model of the piezoelectric laminated cantilever

表1 压电层合悬臂梁压电层材料参数Tab.1 Material properties of the piezoelectric layers
将图2所示悬臂梁等分为5个单元,每个单元20个广义位移自由度,对应每个单元的每层压电层有1个电势自由度。在梁的上下表面施加1V的电势时,悬臂梁垂直方向的变形如表2所示。本文模型的计算结果与参考文献结果吻合较好,说明本文的压电层合单元模型是可行的。

表2 单位电势时悬臂梁位移Tab.2 Deflections of the cantilever produced by a unit voltage
5.2 基于精细积分的简谐激励作用下悬臂梁动力响应数值模拟
如图3所示的压电层合悬臂梁,上、下层为压电层,中间层基体结构为钢。单元划分以及节点编号、单元编号如图4所示。各层材料参数如表3所示。
模态计算得到图3中悬臂梁的前4阶固有频率为8.80 Hz、55.15 Hz、155.86 Hz和311.91 Hz。
图3所示悬臂梁,自由端作用力F=0.2sin188.4 tN,Rayleigh阻尼比α=3和β=1×10-4。图4为节点编号及单元编号。图5为比较精细积分法与Wilson-θ法计算悬臂梁自由端的位移响应曲线。
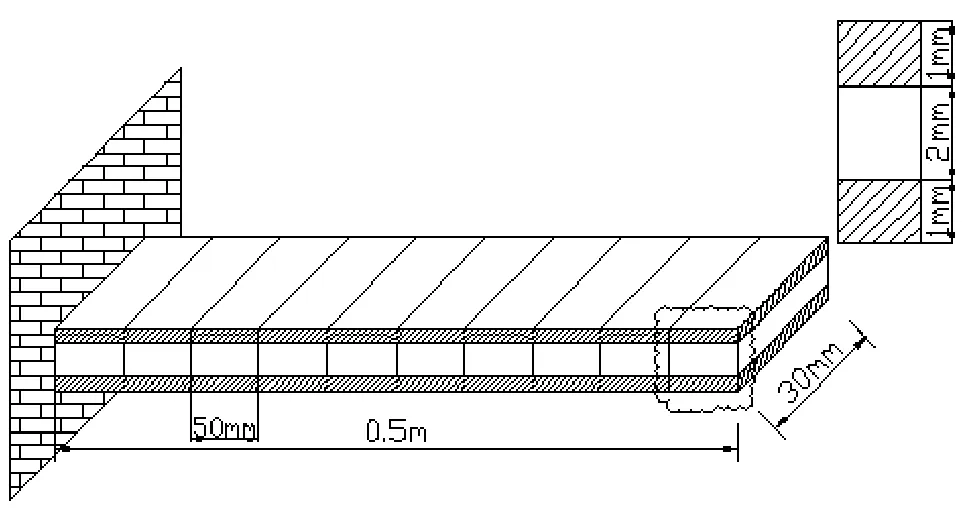
图3 压电层合悬臂梁Fig.3 Piezoelectric laminated cantilever
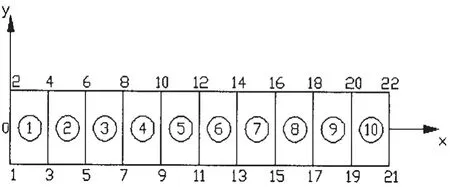
图4 节点编号及单元编号Fig.4 Node number and element number

表3 压电层合悬臂梁各层材料参数Tab.3 Material properties of each layer of the piezoelectric laminated cantilever
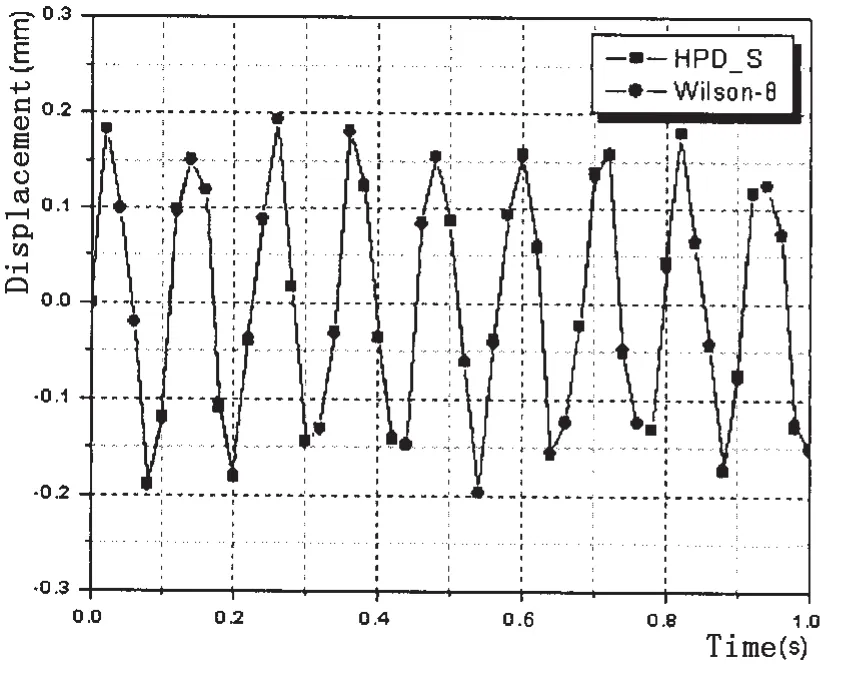
图5 两种算法计算得到的时域位移响应Fig.5 Tip deflection in time domain by the two methods
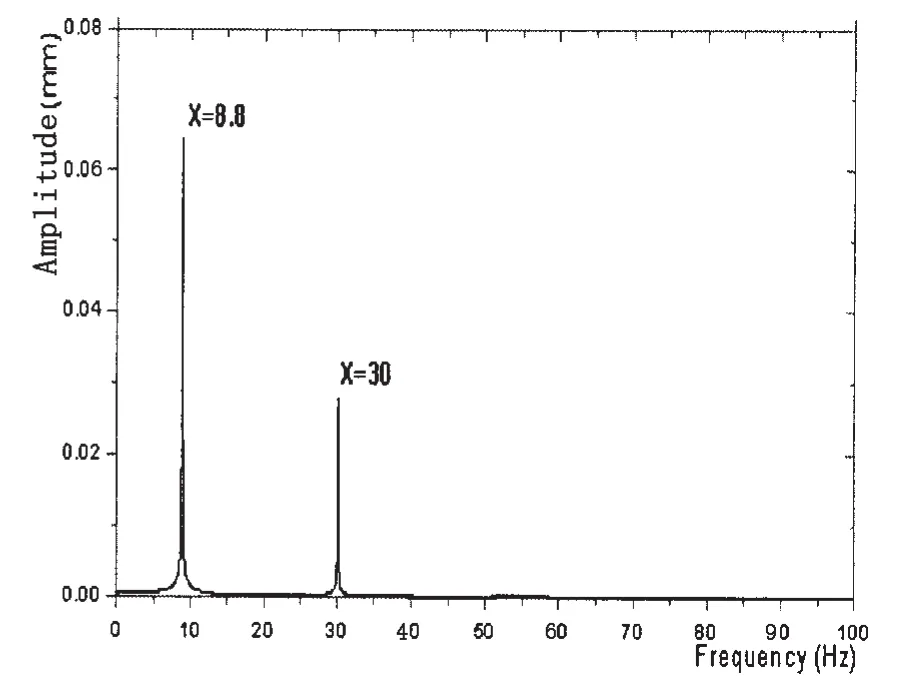
图6 两种算法计算得到的频域位移响应Fig.6 Tip deflection in frequency domain by the two methods
从图5可以看出,两种算法计算结果在初始阶段几乎是一样的。对其进行FFT,转化到频域,得到图6,从中可以看出,频域响应主要集中在悬臂梁的一阶固有频率和激励频率处。
5.3 基于精细积分的脉冲激励作用下悬臂梁动力响应数值模拟
同上如图3所示悬臂梁,在悬臂梁自由端作用0.2 N的瞬时激励,作用时间为1 ms。不考虑阻尼,悬臂梁自由端位移响应曲线如图7所示。
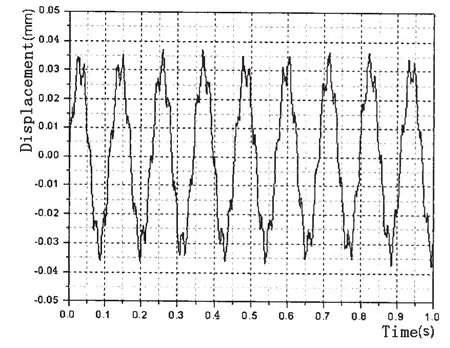
图7 无阻尼自由振动时域位移响应Fig.7 Displacement response of free vibration without damping in time domain
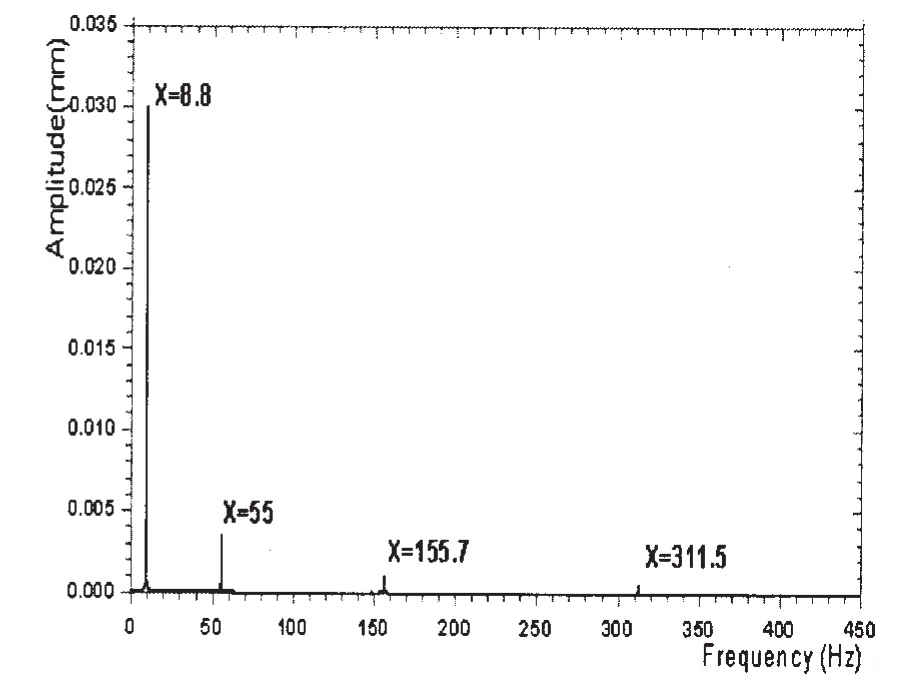
图8 无阻尼自由振动频域位移响应Fig.8 Displacement response of free vibration without damping in frequency domain
图7所示为悬臂梁的自由端受脉冲激励时自由端的时域位移响应曲线,对其进行FFT,得到图8所示的频域位移响应曲线。从图8可以看出,由脉冲激励得到的悬臂梁的前四阶固有频率与前面模态计算得到的固有频率吻合。
5.4 瞬时激励作用下悬臂梁振动LQR控制的数值模拟
同上如图3所示悬臂梁,在悬臂梁的自由端作用0.2 N的瞬时激励,作用时间为1 ms,Rayleigh阻尼比为α=3,β=1×10-4。① 系统自由振动;② 0.5 s开始控制,权系数Q=5×109,两种状态下悬臂梁自由端位移响应曲线如图9所示。
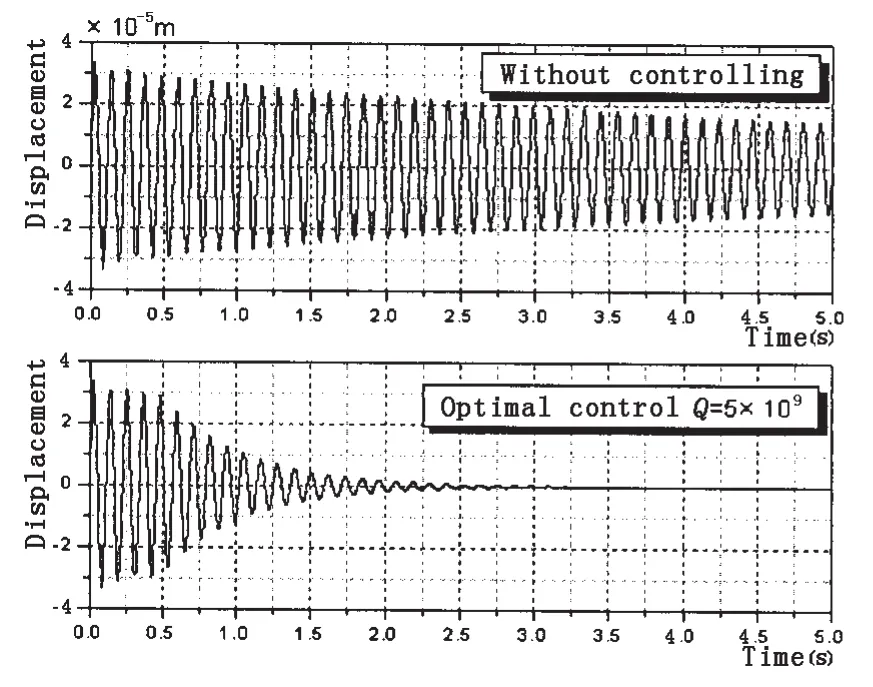
图9 控制与否悬臂梁自由端位移响应比较Fig.9 Comparison of tip displacements of the cantilever with or without controlling
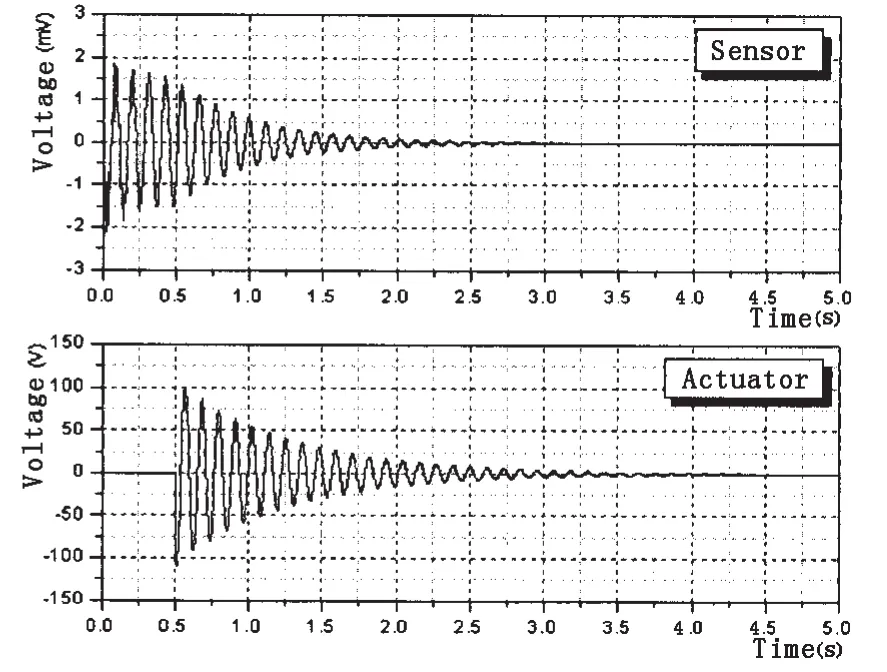
图10 控制后1号单元传感层和作动层电势Fig.10 Voltages of sensor and actuator in the first element with controlling
由上例可知,悬臂梁受瞬时激励自由振动时,一阶模态占主要成分。而悬臂梁以一阶模态振动时,图4中1号单元的传感层电势最大,故这里只输出1号单元的传感层和作动层的电势,如图10所示。从图9可以看出,0.5 s开始控制后,悬臂梁自由端的振动幅值快速衰减,在2.5 s内达到平衡位置。图10可以看出,随着振动的衰减,传感层测得的电势变小,作动层的控制电势也随之减小。
5.5 受简谐激励的悬臂梁振动LQR控制
同上如图3所示悬臂梁,悬臂梁自由端受简谐力F=0.2sin3 140 tN,Rayleigh阻尼比α=3和β=1×10-4。① 不考虑控制;②0.5 s开始控制,权系数Q=1010,两种状态下悬臂梁自由端位移响应曲线如图11所示。1号单元传感层和作动层电势如图12所示。

图11 控制与否悬臂梁自由端位移响应比较图Fig.11 Comparison of tip displacements of the cantilever damping in time domain
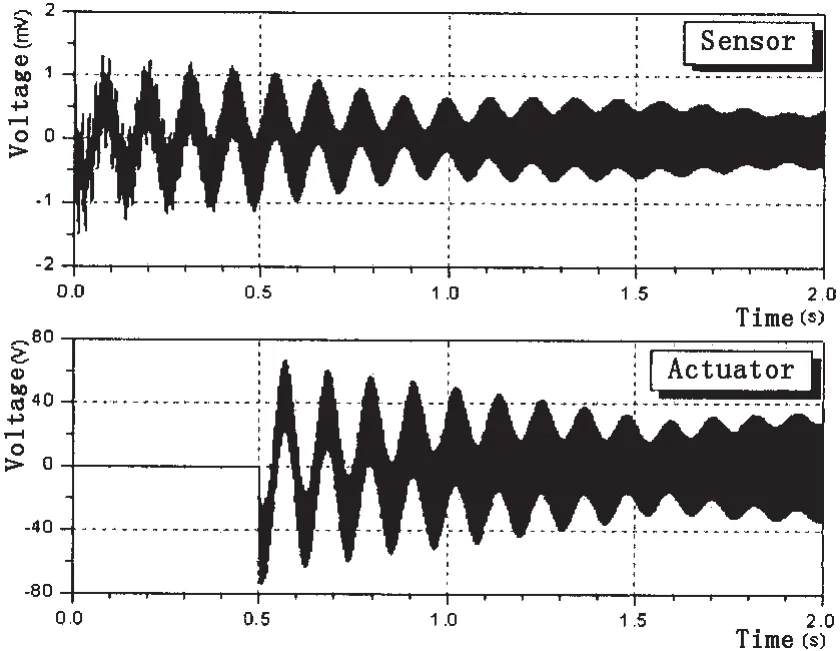
图12 控制后1号单元传感层和作动层电势Fig.12 Voltages of sensor and actuator in the first element with controlling
从图11可以看出,0.5 s时刻开始控制后,悬臂梁自由端振动的位移幅值明显衰减。从图12可以看出,随着振动幅值的衰减,传感器测得的电势以及控制所需要的电势都呈衰减趋势。
5.6 LQR控制的权系数矩阵对控制效果的影响
同上例,改变最优控制目标函数中的权系数矩阵。分别计算Q=5×109和Q=1×1011,得到0.5 s开始控制时悬臂梁自由端时域位移响应曲线,以及1号单元作动层的电势。
由图13和图14的曲线可以看出,增大权系数矩阵Q,系统能更快达到稳定状态,且稳态振动时的幅值更小,但是,所需要的控制电势相应地会增大。
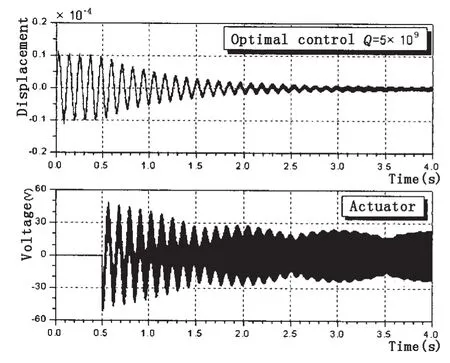
图13 位移响应以及作动层电势Q=5×109Fig.13 Tip displacement and voltage of the first actuator while Q=5×109
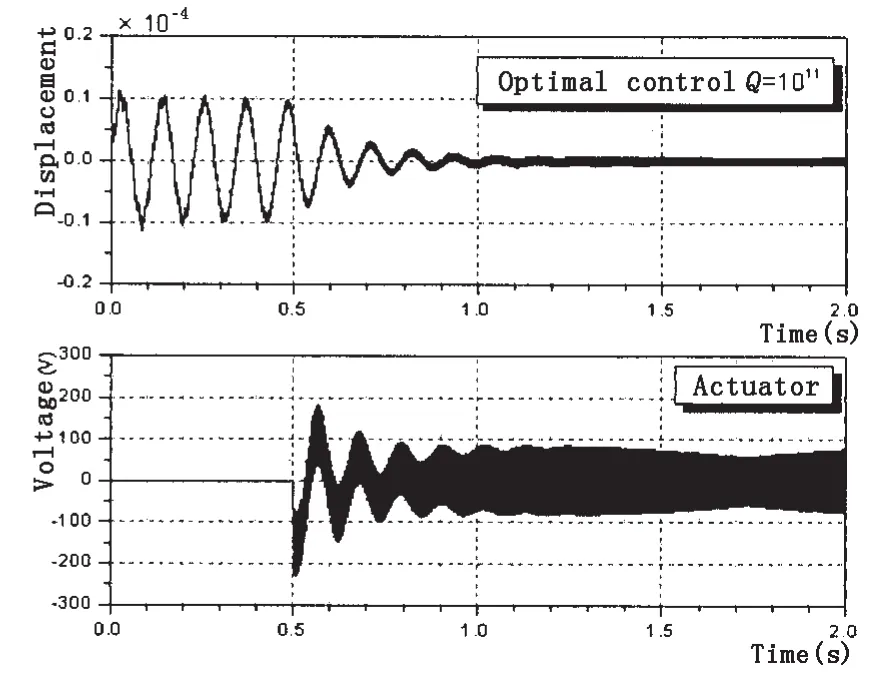
图14 位移响应以及作动层电势Q=1×1011 Fig.14 Tip displacement and voltage of the first actuator while Q=1×1011
6 结 论
本文基于Mindlin一阶剪切变形理论推导的4节点的四边形压电层合单元是准确可行的,能很好地模拟压电层合柔性结构的力学行为。状态空间模型能很好地实现系统的反馈控制,便于比较考虑控制与否以及不同的控制参数对系统最终状态响应的影响。用LQR方法设计的位移反馈控制器,在数值模拟上能很好地抑制压电层合悬臂梁受瞬时激励或简谐激励下的振动位移响应,明显缩短了系统达到平衡位置或稳态振动的时间,降低了稳态振动时的位移响应幅值。最优控制目标函数中权系数矩阵的选取对控制效果以及控制所需能量的影响很大,Q值越大,控制效果越好,控制所需的能量越大。本文对含分布式压电传感器和作动器的悬臂梁振动控制的研究说明了压电智能结构在舰船结构振动主动控制中运用的可行性。
[1]Song G,Sethi V,Li H N.Vibration control of civil structures using piezoceramic smart materials:A review[J].Engineering Structures,2006,28:1513-1524.
[2]Crawley E F,decuis J.Use of piezoelectric actuators as element of intelligent structures[C]//AIAA/ASME/ASCE/AHS 27th Structures,Structural Dynamics and Materials Conference,May 19-21,1986,TX,USA,1986.
[3]Tzou H S,Teng C I.Distributed piezoelectric sensor/actuator design for dynamic measurement/control of distributed parameter systems:A piezoelectric finite element approach[J].Journal of Sound and Vibration,1990,138(1):17-34.
[4]Ray M C,Bhattacharyya R,Samanta B.Exact Solutions for Static Analysis of Intelligent Structures[J].AIAA Journal,1993,31(9):1684-1691.
[5]Samanta B,Ray M C,Bhattacharyya R.Finite element model for active control of intelligent structure[J].AIAA Journal,1996,34(9):1885-1893.
[6]Sung Yi,Shih Fu Ling,Ming Ying.Large deformation finite element analyses of composite structures integrated with piezoelectric sensors and actuators[J].Finite Elements in Analysis and Design,2000,35:1-15.
[7]Simoes-Moita.Active control of adaptive laminated structures with bonded piezoelectric sensors and actuators[J].Compute&Structures,2004,82:1349-1358.
[8]Narayanan S,Balamurugan V.Finite element modeling of piezolaminated smart structures for active vibration control with distributed sensors and actuators[J].Journal of Sound and Vibration,2003,262:529-562.
[9]Jiang Jianping,Li Dongxu.A new finite element model for piezothermoelastic composite beam[J].Journal of Sound and Vibration,2007,306:849-864.
[10]Merek Pietrzakowski.Piezoelectric control of composite plate vibration:Effect of electric potential distribution[J].Computers and Structures,2008,86:948-954.
[11]Kepler R G.Piezoelectricity,pyroelectricity and polyvinylidene in organic materials(review)[J].Annual Review of Physical Chemistry,1978,29:497-518.
[12]Kepler R G,Anderson R A.Piezoelectricity and pyroelectricity in polyvinylidene fluoride[J].Journal of Applied Physics,1978,49:4491-4498.
[13]Lee C K.Theory of laminated piezoelectric plates for the design of distributed sensors/actuators.Part 1:Governing equations and reciprocal relationships[J].Journal of the Acoustical Society of America,1990,87(3):1144-1158.
[14]Tiersten H F.Linear piezoelectric plate vibrations[M].New York:Plenum Press,1969.
[15]Tzou H S,Tseng C I.Distributed piezoelectric sensor/actuator design for dynamic measurement/control of distributed parameter systems:A piezoelectric finite element approach[J].Journal of Sound and Vibration,1990,138(1):17-34.
[16]Tzou H S.Piezoelectric shells:distributed sensing and control of continua[M].Netherlands,Kluwer Academic Publishers,1993.
[17]Tzou H,Ye S R.Analysis of piezoelastic structures with laminated piezoelectric triangle shell element[J].AIAA Journal,1996,34(1):110-115.
[18]Gomes M.Alexandra.Modelling and optimization of electromechanical adaptive structures[D].MSc.Thesis,Instituto Superior Tecnico,Technical University of Lisbon,Portugal,1997.(in Portuguese)

