泥沙颗粒跃移运动机理

白玉川，陈有华，韩其为

泥沙颗粒跃移运动机理

白玉川1,2，陈有华2，韩其为2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 天津大学河流海岸工程泥沙研究所，天津 300072)

水流中泥沙颗粒的跳跃运动是推移质运动的重要形式，根据泥沙颗粒运动过程的受力分析，建立了忽略颗粒旋转和紊动影响的泥沙颗粒跃移运动模型，并采用数值计算方法，求解了跃移运动方程，得到了跃移运动参数(跃移长度、跃移高度、跃移速度)的统计特性，所得结论与实验资料吻合较好；通过对数值计算结果回归分析，得到了跃移运动参数以及输沙率的数学表达式，对于了解推移质运动机理有重要的意义．

推移质；跃移；输沙率

泥沙颗粒在水流作用下发生3种运动模式：跃移、滚动(滑动)和悬移．床面泥沙以滚动、滑动还是跃移的方式运动，取决于水流强度和床面特性，当床面切应力超过临界起动应力时，床沙开始以滑动或滚动形式运动[1-4]．如果床面切应力继续增加，颗粒开始从床面跃起进入跳跃运动状态，这些以滑动、滚动和跳跃形式运动的泥沙称为推移质．关于推移质的运动形态，文献[5-8]认为跳跃是推移质的主要形式，而文献[2，9-10]则认为泥沙起动的初始阶段以及当水流强度较小时，床面剪切力较小，泥沙则主要以滚动、滑动的形式运动．笔者已对以滚动、滑动形式运动的接触型推移质进行了研究，并取得了一定的成果[11-12]．这里针对跃移型推移质进行研究，以达到全面了解推移质运动的目的．

对于颗粒的跳跃运动，许多学者都做了大量的研究工作，Einstein[13]基于水槽实验得出推移质层厚度大约是2D，跃高大约是100D；Van Rijn[3]建立了颗粒单步跃移模型，利用上述研究者的实验数据检验此模型，证明其可适用于低雷诺数水流条件；惠遇甲等[14]利用高速摄像技术测量了床面附近颗粒的运动状态，并给出了滑动、滚动、跃移以及悬移各占的比例；Nino等[4,15]利用高速摄像技术测量了跃移轨迹并建立了二维连续跳跃模型；文献[16-19]对颗粒的跃移运动进行了一系列系统的研究，利用实时图像显示技术和高速摄像技术测量了跃移轨迹和速度，分别建立了单步跳跃模型、多颗粒连续跳跃模型以及三维连续跳跃模型．笔者分别建立泥沙颗粒跳跃运动起步阶段和飞行阶段的运动模型，并在此基础上分析研究跃移运动参数的统计特性以及推移质输沙规律．

1 跃移型推移质运动理论模型

1.1泥沙受力模型

当水流流过松散河床时，单颗粒床面泥沙在水流的作用下，主要承受上举力LF、拖曳力DF、重力W．考虑单向流运动情况，设泥沙在水流作用下移动的纵向和垂向速度分别为u、v，水流作用在床面沙粒上的流速为bU，则上举力LF、拖曳力DF、重力W的表达式分别为

式中：DC为泥沙颗粒拖曳力阻力系数；LC为泥沙颗粒上举力系数；D为泥沙粒径；ρ为水的密度；γ、sγ分别为水和泥沙的容重；1A、2A和3A均为泥沙颗粒面积修正系数．

1.2跃移型推移质运动的动力学方程

1.2.1 跃移起步段(初始段)

在力学分析的基础上，根据牛顿第二定律，建立泥沙跃移起步阶段运动方程为

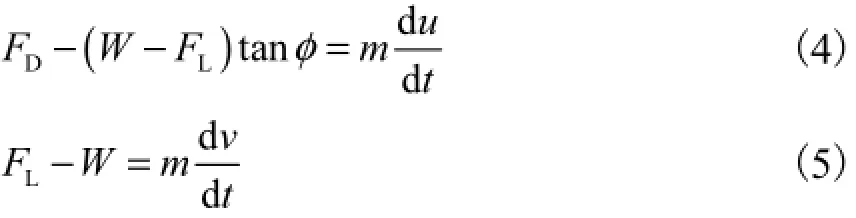
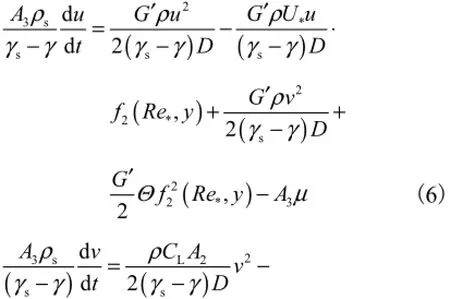
式(6)、式(7)的各项系数具有明确的物理含义，为此引入如下物理概念[12-13]：

阻力参数

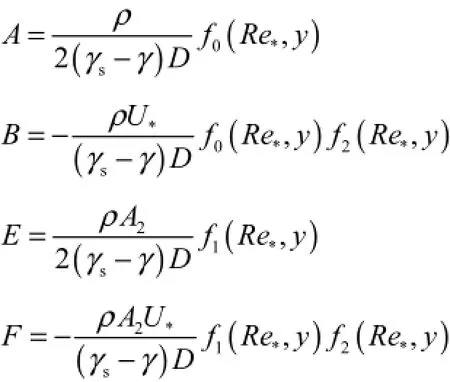
颗粒运动的临界参数

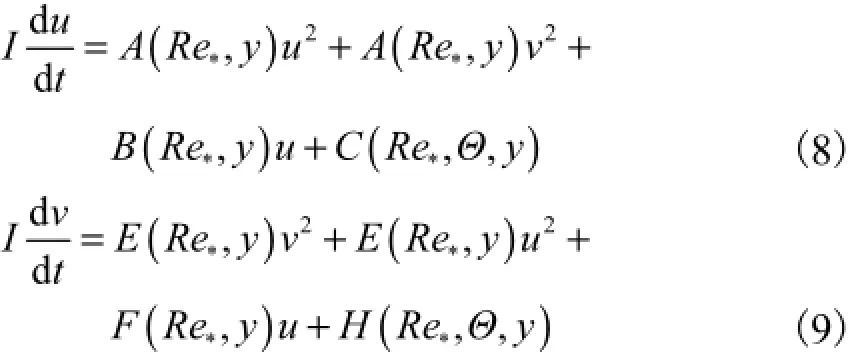
1.2.2 跃移飞行段

跃移型推移质跃移飞行阶段，摩擦力等于零，运动方程可写为

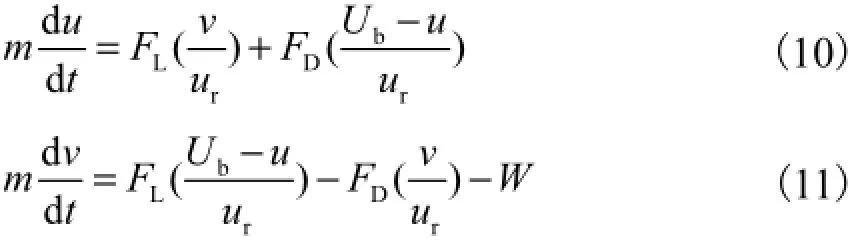
式中：相对流速ur=[(Ub-u)2+v2]0.5；(Ub-u)/ur和v/ur分别表示阻力与水流方向夹角的余弦和正弦．

2 泥沙运动临界状态分析

2.1临界起动状态

当泥沙颗粒处于临界起动状态时，此时可以近似忽略其垂向运动，只考虑纵向运动，纵向运动速度U=0，加速度．由运动方程式(8)可以得出C=0，由此可以得到

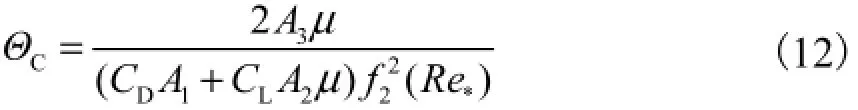
很容易看出，式(12)其实就是代表着泥沙起动的希尔兹(Sheilds)曲线．

2.2临界扬动状态

当泥沙处于由静止扬起临界状态时，此时可以忽略其纵向运动，只考虑垂向运动，垂向运动速度v=0，加速度=0，由运动方程式(9)得出H=0，进一步可以得到

以沙粒雷诺数*Re为横坐标、希尔兹参数Θ为纵坐标绘出泥沙颗粒处于临界状态时的关系曲线，如图1所示．

图1 泥沙运动临界状态变化曲线Fig.1 Sediment motion critical curves

3 跃移颗粒运动状态分析

3.1方程数值求解

跃移颗粒飞行阶段运动方程是不能直接求得解析解的，必须借助于数值计算方法进行求解．采用四阶龙格-库塔法对方程组计算可得出轨迹、跃高和跃长等参数，在计算过程中做了如下的假定，同时对一些参数的确定方法也加以说明．

1)假定

计算中的颗粒是粒径为D的圆球，且为均匀密度．

关于跃移初始速度，文献[20]认为u0/u*和v0/u*近似等于2，文献[21]认为跃移初始速度在u*∼2.5u*之间，文献[3]采用了2u*，文献[17]的分析中采用了2.5u*．基于上述前人的研究成果，本文计算中采用=2.5u*，=2.5u*．

3)初始位置

床沙颗粒在水流作用下开始运动，只有其跃起一定高度以后才认为是跳跃运动．胡春宏等[22]认为，当颗粒在运动中的最高点离开床面超过1,D高度后，即为跃移运动；Van Rijn[3]的研究中跃移初始位置采用0.6,D，初始位置为颗粒重心距床面的距离，因此与文献[14]的研究结果是一致的，故本文中跃移初始位置亦采用0.6,D．

4)阻力系数DC和上举力系数LC

阻力系数采用

上举力系数LC受颗粒大小、形状、旋转角速度以及水流条件影响，一般可当作常量处理[23]，文献[4，16-19]的分析中均采用文献[23]中建议的L0.2C=，本文分析中也采用上述结果．

5)采用对数流速分布

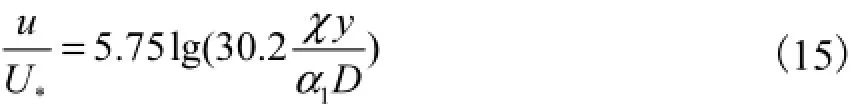
式中：12α≈；χ为与沙粒雷诺数有关的函数．

3.2量纲分析

为了对跃移运动参数进行统计特性分析，同时便于与别人的实验资料进行比较，需要对颗粒跃移运动所涉及的水流条件和颗粒参数无量纲化．反映颗粒跃移运动的参数主要包括水深H、坡降J、水的密度ρ、泥沙粒径D、跃移泥沙密度sρ、运动黏性系数μ、颗粒表面粗糙度sk、床沙粒径bD以及重力加速度g．利用π定理，可得无量纲方程[17]，即

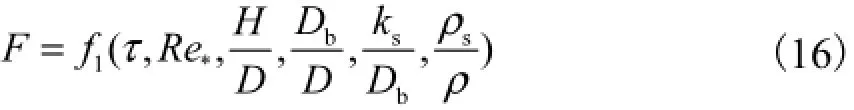
式中：F为无量纲跃移运动参数，包括跃高、跃长以及跃移速度；τ 为无量纲切应力，为摩阻流速，；*Re为颗粒雷诺数，．由于H≫D，Db≫ks，同时假定D=Db，则可以略去这3项，将τ、*Re合并，略去*U，可得参数．用(U*-U*c)代替U*．用参数代替τ，因此式(16)可以简化为

3.3数值计算结果及分析

数值计算所得几组典型跃移轨迹见图2和图3．将数值计算所得跃移特征(包括跃高、跃长、跃移速度)与文献[4，16-17]的实验数据进行比较，跃高、跃长、跃移速度与*T的关系分布见图4～图6．可以看出，无量纲跃高、跃长均随*D和*T的增加而增大，但是当*T较大时，随*D的增幅程度变得不太明显．这说明，当水流强度较大时，无量纲跃高、跃长与颗粒形状的关系不显著．文献[5，24]指出，跃长仅与颗粒形状和大小有关，与水流强度无关，而本文中的分析结果则说明此结论只适用于强水流情况，在水流强度较低时，跃长是与水流强度有关的．由图7可以看出，数值计算得到跃高点长(跃移颗粒达到最高点时对应的跃长)约占整个跃长的35%，文献[17]的实验结果约为40%，文献[14]的研究结果为30%．

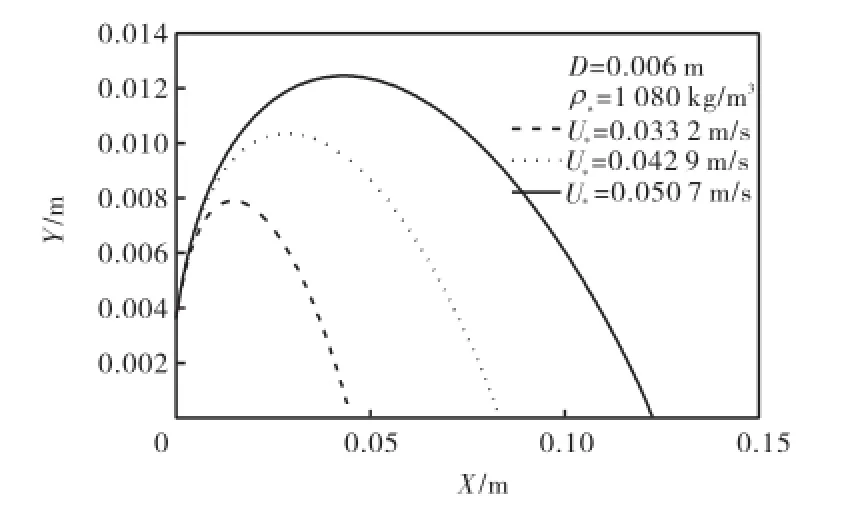
图2 跃移运动轨迹ⅠFig.2 Typical saltation trajectoryⅠ

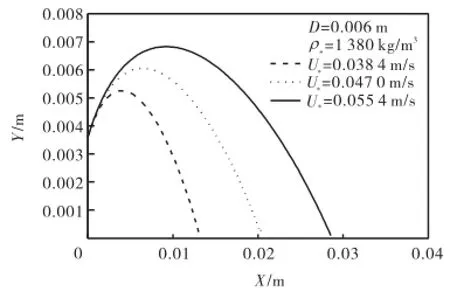
图3 跃移运动轨迹ⅡFig.3 Typical saltation trajectoryⅡ

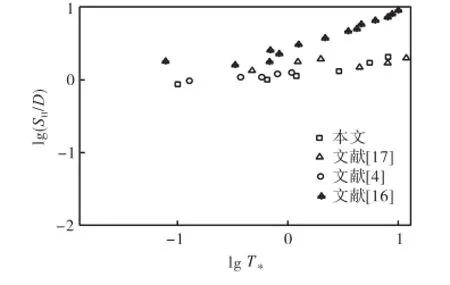
图4 无量纲跃高SH/D与T*的关系Fig.4 Relations between dimensionless saltation height SH/D and T*

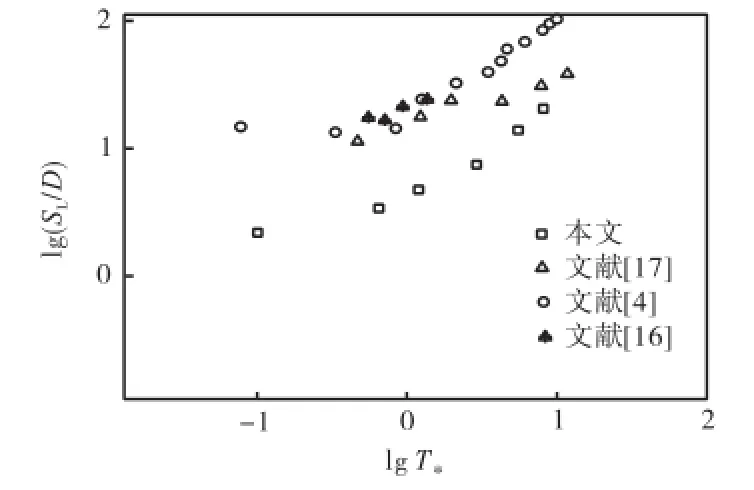
图5 无量纲跃长SL/D与T*的关系Fig.5 Relations between dimensionless saltation length SL/Dand T*

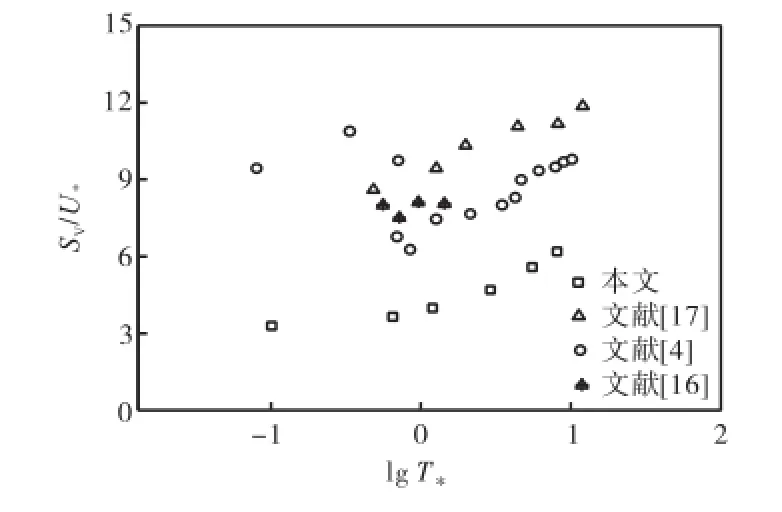
图6 无量纲跃移速度SV/U*与T*的关系Fig.6 Relations between dimensionless saltation velocitySV/U*andT*

图7 跃高点长L1/SL与T*的关系Fig.7 Relations between location of peak of saltation trajectory L1/SLand T*

根据数值计算结果，得到跃移运动参数的回归方程为

式中HS、LS和VS分别为跃高、跃长和跃移速度．

3.4推移质输沙率

推移质输沙率表示为

式中bC为推移质浓度．根据文献[17]，bC可表示为

将式(18)、式(20)、式(22)代入式(21)中得推移质单宽输沙率为

由于文献[25-26]中的公式均是基于泥沙跳跃机理建立的，因此将式(23)与文献[25-26]中的2个公式进行比较，如图8所示．从图8中可以看出Yalin公式[25]计算结果明显偏小，式(23)在低强度下计算结果较文献[25-26]中的公式计算结果偏大，而随着水流强度增大，计算结果与文献[25-26]中的公式计算结果吻合程度较好．

图8 数值计算所得推移质输沙率公式与文献[25-26]中公式比较Fig.8 Comparison between simulated bed load transport rate and formulae in Refs.[25-26]

4 结 论

(1) 针对跃移型推移质泥沙运动，从泥沙颗粒典型受力出发，分别建立了床面层内跃移质运动起步阶段和飞行阶段的理论模型．

(2) 根据跃移颗粒起步阶段运动方程特性，从理论上推导得到了泥沙由静止起动、扬动的函数表达式，从理论上解释了希尔兹曲线的物理意义．

(3) 利用数值计算方法求得的跃移轨迹与前人实验资料吻合较好，并且从中可以看出：颗粒跃移轨迹形状类似弹道，颗粒的跃移高度、长度以及跃移速度均随水流强度的增大而增大，在相同的水流强度下，粒径大的颗粒的跃高、跃长以及跃移速度要比粒径小的大；当水流强度较低时，无量纲跃高、跃长均随*D的增大而增大，跃高、跃长都与水流强度有关；当水流强度较大时，无量纲跃高、跃长随*D的变化不太显著；跃高点大约处于1/3的跃长处.

(4) 根据数值计算结果，回归得到了跃移运动参数(跃高、跃长、跃移速度)的数学表达式，并进一步得到了相应的推移质输沙率公式，将所得输沙率公式与其他公式对比，说明其可以反映实际输沙情况.

［1］ 钱 宁，万兆惠. 泥沙运动力学[M]. 北京：科学出版社，1983.

Qian Ning，Wan Zhaohui．Kinematical Mechanics of Sediment[M]. Beijing：Science Press，1983(in Chinese).

［2］ Peng Gao. Transition between two bed-load transport regimes：Saltation and sheet flow [J]. Journal of Hydraulic Engineering，ASCE，2008，134(3)：340-348.

［3］ Van Rijn L C. Sediment transport(Part I)：Bed load transport[J]. Journal of Hydraulic Engineering，ASCE，1984，110(10)：1431-1456.

［4］ Nino Y，Garcia M. Experiments on saltation of sand in water[J]. Journal of Hydraulic Engineering，ASCE，1998，124(10)：1014-1025.

［5］ Einstein H A. Formula for the transportation of bedload[J]. Transactions of the American Society of Civil Engineers，1942，107：561-597.

［6］ Sekine M，Kikkawa H. Mechanics of saltating grainsⅡ[J]. Journal of Hydraulic Engineering，ASCE，1992，118(4)：536-558.

［7］ Wiberg P L，Smith J D. Calculation of the critical shear stress for motion of uniform and heterogeneous sediments[J]. Water Resources Research，1987，23(8)：1471-1480.

［8］ Wiberg P L，Smith J D. Model for calculation bed load transport of sediment[J]. Journal of Hydraulic Engineering，ASCE，1989，115(1)：101-123.

［9］ 韩其为，何明民. 泥沙起动规律及起动流速[M]. 北京：科学出版社，1999.

Han Qiwei，He Mingmin. The Incipient Disciplinarian and Incipient Velocity of Sediment[M]. Beijing：SciencePress，1999(in Chinese).

［10］ Mazumder B S，Anindita B，Satya P O. Near-bed particle motion due to turbulent flow using image-processing technique[J]. Journal of Flow Visualization and Image Processing，ASCE，2008，15(1)：1-15.

［11］ Bai Yuchuan，Xu Haijue，Xu Dong，et al. Nonlinear dynamical characteristics of bed load motion[J]. Science in China (Series E)：Technological Sciences，2006，49(3)：365-384.

［12］ Xu Haijue，Bai Yuchuan，Ng Chiu-On. Nonlinear mechanism of bed load transport[J]. Transactions of Tianjin University，2009，15(2)：126-129.

［13］ Einstein H A. The Bed-Load Function for Sediment Transport in Open Channel Flows[M]. Washington，USA：Department of Agriculture，Soil Conservation Service，1950.

［14］ 惠遇甲，胡春宏. 水流中颗粒跃移的运动学特征[J].水利学报，1991，4(12)：59-64.

Hui Yujia，Hu Chunhong. Saltation characteristics of particle motions in water[J]. Journal of Hydraulic Engineering，1991，4(12)：59-64(in Chinese).

［15］ Nino Y，Garcia M. Gravel saltation (2)：Modeling[J]. Water Resources Research，1994，30(6)：1915-1924.

［16］ Lee Hongyuan，Hsu Insong. Investigation of saltating particle motions[J]. Journal of Hydraulic Engineering，ASCE，1994，120(7)：831-845.

［17］ Lee Hongyuan，Chen Yenhsu，You Jiingyun，et al. Investigations of continuous bed load saltating process[J]. Journal of Hydraulic Engineering，ASCE， 2000，126(9)：691-700.

［18］ Lee Hongyuan，You Jiingyun，Lin Yingtien. Continuous saltating process of multiple sediment particles[J]. Journal of Hydraulic Engineering，ASCE，2002，128(4)：443-450.

［19］ Lee Hong-Yuan，Lin Ying-Tien，You Jiingyun，et al. On three-dimensional continuous saltating process of sediment particles near the channel bed[J] Journal of Hydraulic Research，ASCE，2006，44(3)：374-389.

［20］ Abbott J E，Francis J R C. Saltation and suspension trajectories of solid grains in a water stream[J]. Philosophical Transactions of the Royal Society，1977，284(1321)：225-254.

［21］ White B R，Shulz J C. Magnus effect in saltation[J]. Journal of Fluid Mechanics，1977，81(3)：497-512.

［22］ Hu Chunhong，Hui Yujia. Bed-load transport(Part I)：Mechanical characteristics[J]. Journal of Hydraulic Engineering，ASCE，1996，122(5)：245-261.

［23］ Wiberg P L，Smith J D. A theoretical model for saltating grains in water[J]. Journal of Geophysical Research，1985，90(4)：7341-7354.

［24］ Einstein H A，E1-Sammi E A. Hydrodynamic forces on a rough wall[J]. Reviews of Modern Physics，1949，21(3)：520-524.

［25］ Yalin M S. Mechanics of Sediment Transport [M]. New York：Pergamon Press，1972.

［26］ Engelund F，Fredsoe J. A sediment transport model for straight alluvial channels[J]. Nordic Hydrology，1976，7(5)：293-306.

Bed Load Saltation Movement Mechanism

BAI Yu-chuan1,2，CHEN You-hua2，HAN Qi-wei2
(1. State Key Laboratory of Hydraulic Simulation and Safety，Tianjin University，Tianjin 300072，China；2. Institute of Sediment on River and Coast Engineering，Tianjin University，Tianjin 300072，China)

Saltation of solid grains is an important form of bed load transport. Force of movement particle was studied and sediment saltation movement model neglecting particle rotation and turbulence effects was established on the basis of the results. Using numerical calculation method to solve the motion equation, get the statistical properties of saltation parameters (height of saltation, length of saltation, velocity of saltation), which agreed well with the previous experimental data. Through regression analysis, the mathematical expressions of saltation parameters and sediment transport rate were obtained, which is very important for studying the mechanics of bed load transport and bed load transport rate.

bed load；saltation；transport rate

TV142

A

0493-2137(2012)03-0196-06

2011-06-29；

2011-11-16.

国家自然科学基金创新研究群体科学基金资助项目(51021004)；国家自然科学基金资助项目(50979066)．

白玉川（1967— ），男，教授．

白玉川，ychbai@tju.edu.cn.